直线钢腱配筋率与弹性模量的关系
弹性模量是材料在外力作用下产生的应力与伸长或压缩弹性形变之间的关系。亦称杨氏模量。其数值为试样横截面所受正应力与应变之比。它表征材料抵抗变形的能力,与材料的强度、变形、断裂等性能均有关系,是材料的重要力学参数之一。弹性模量是结构分析的重要参数,对于钢筋混凝土结构,在结构分析时弹性模量如何取值的问题,还没有完全解决 一种观点认为钢筋混凝土的配筋率很小,钢筋的影响可以忽略不计,可近似取素混凝土的弹性模量值。但大多数学者仍认为钢筋混凝土弹性模量的取值还是应该计入钢筋的影响。针对钢筋混凝土这种复合材料,刘庆涛提出了运用有限元法计算悬臂梁的挠度,根据挠度与弹性模量之间的关系间接获得复合材料弹性模量的方法。配筋率对钢筋混凝结构弹性模量的影响是明显的,在结构动力计算和超静定结构的内力计算中,配筋率较高时,若忽略钢筋对弹性模量的影响,会对计算结果造成误差。弹性模量与配筋率基本呈线性关系,钢筋混凝土复合材料的弹性模量近似取钢筋和混凝土两种材料截面面积的加权平均值是合理的,在合理的配筋率范围内,误差不超过5%。 2100433B
直线钢腱造价信息
混凝土断裂是混凝土材料由于裂缝的形成和发展造成的破坏。混凝土由于施工期温度控制不当或其他原因,会出现微细裂缝。在工作期间,由于荷载和温度变化等因素,这些微细裂缝会发展,部分连通、合并成一条或多条宏观裂缝并逐步扩展,最终可能导致结构破坏。在裂缝尖端两侧混凝土表面粘贴的应变片显示,在混凝土开裂之前,随着荷载的增加,裂缝尖端两侧的应变也随着增加,属于拉应变;但在某一时刻,当应变增加到峰值时,裂缝尖端处的混凝土由于应力集中而开裂,此时裂缝两侧的混凝土变形得到释放,在曲线上反映为拉应变不再增加,而荷载继续增加。由于缝端混凝土的开裂,其附近的拉应力卸载,拉应变减小,甚至出现压应变,应变峰值所对应的荷载即为起裂荷载。随着配筋率的逐渐增大,试件发生失稳破坏时,钢筋的约束力也在逐渐增大,钢筋对混凝土的约束作用也在逐渐增强,但是所有钢筋均没有屈服,属于超筋破坏。临界有效裂缝长度随着配筋率的增大而逐渐减小,说明超筋破坏时,试件的延性随着配筋率的增大而逐渐降低。钢筋混凝土试件的起裂断裂韧度与配筋率无关,是材料固有的一个参数,而失稳断裂韧度随着配筋率的增大而逐渐增大。钢筋混凝土试件的延性随着配筋率的增大而逐渐降低。
混凝土是实际工程中应用最广泛的建筑材料之一,其受力的过程也就是裂缝产生和扩展的过程,一旦混凝土产生裂缝,在荷载等因素的影响下,这些裂缝会进一步扩展,最终导致整个结构的破坏。为了抑制裂缝的进一步扩展,防止混凝土结构发生脆断现象,通常在混凝土中埋入钢筋、钢纤维等抗拉性能好的材料,以弥补混凝土抗拉能力的不足,提高结构的抗破坏能力。钢筋比,又称面积配筋率,钢筋混凝土构件中受力钢筋的总截面积与构件截面有效面积的比值,以百分比表示。中国“规范”对一般构件的最大、最小配筋率均有规定。构件中配置的钢筋截面面积与规定的混凝土截面面积的比值。
最小配筋率式为保证钢筋混凝土截面所能抵抗的弯矩不致小 于它的抗裂弯矩而规定的配筋率的下限值,以免构 件开裂后钢筋立即屈服而发生脆性破坏。欧洲混凝 土协会-国际预应力混凝土协会 (CEB-FIP)模式规 范还根据裂缝宽度的限值规定混凝土受拉区的最小 配筋率,以便保证结构的使用性能良好。受弯构件的配筋率达到相应于混凝土即将破坏时的配筋率,称为最大配筋率。
直线钢腱配筋率与弹性模量的关系常见问题
-
型钢的弹性模量为2.1 ×10^7N/cm²。弹性模量定义:一般地讲,对弹性体施加一个外界作用,弹性体会发生形状的改变(称为“应变”),“弹性模量”的一般定义是:应力除以应变。材料在...
-
力,作为应变的函数,它和应变的比率称为弹比模量。它是应力——应变曲线直线部分的斜率。切线弹性模量的定义是应力——应变曲线在任意点的斜率。割线弹性模量则等于应力除以该应力值所对应的应变或者应力除以应变。...
-
弹性模量是指材料在加载过程中弹性范围内的应力应变曲线斜率(是常数E=Δσ/Δε=σ/ε),材料进入塑性变形后卸载,卸载过程中应力应变变化的斜率是回弹模量(E‘=Δσ/Δε,也是...
直线钢腱配筋率与弹性模量的关系文献

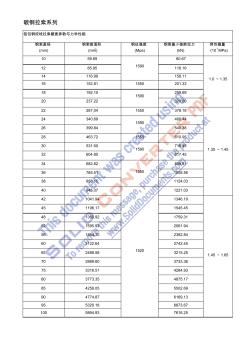 钢铰线拉索弹性模量参数
钢铰线拉索弹性模量参数
碳钢拉索系列 铝包钢绞线拉索截面参数与力学性能 钢索直径 (mm) 钢索断面积 (mm2) 钢丝强度 (Mpa) 钢索最小破断拉力 (kN) 弹性模量 (10 5 MPa) 10 59.69 1590 80.67 1.0~1.35 12 85.95 116.16 14 116.99 158.11 16 152.81 1550 201.33 18 192.15 1590 259.69 20 237.22 320.60 22 287.04 1550 378.18 1.35 ~1.45 24 340.69 1590 460.44 26 399.84 540.38 28 463.72 1550 610.95 30 531.60 1590 718.46 32 604.85 817.45 34 682.82 1550 899.61 36 765.51 1008.56 38 853.15 1124.03
钢腱施拉之前,必须检视所有抓握器等是否装置妥善,否则,冒然施拉。极易造成危险。校正施拉机上拉力表之准确性,使于钢腱伸长量计算之拉力误差在5%以内。
检查无误后,即可将施拉械放至梁施拉端的锚柱外,将穿有钢腱并已装妥抓握器(或铆钉头)的钢钣于施拉械前端的端钣或环钣锁牢。即可准备施拉。
施拉作业,最好于当地气温与梁身混凝土温度相若时施行,如气温低于混凝土温度甚多时。则在前算钢腱伸长量外,虑另加因温度差而增加的伸长量。应注意施拉时钢腱的应力不得超过最低终极强度的80%。
施拉械(tensioning machine)多为油压动力,亦如一般的油压千斤顶(oil jack),其上附有压力表。用以显示施拉的拉力。
在进行预力施拉之前。应先将各钢钢腱拉紧,使其无松弛(slack)或下垂(sag)现象。然后于各钢腱紧贴梁端端模处以油漆作一标记,作为将来计算钢腱伸长量的基准线,同时记录此时施拉械上压力表的拉力读数。作为初读数,并予以推算施拉至应有拉力时的末读数,作属为将来施拉时控制拉力之需。
前述各项作业完成后,始可进行施拉。施拉时启动油压机开关阀。千斤顶即缓缓拉动贴于锚柱面上的钢腱(个别施拉法)或穿有钢腱的厚钢钣,由于各钢腱已与钢钣锁紧,因而施拉之拉力,即透过厚钢钣而均匀分布于各钢腱承受,钢腱受拉时,因其弹性的特性而伸长,此畴时必须贯注全神于施拉械之压力表。待其读数到达预先计算之末读数时。应即停止施拉。并将拉力固定于此末读数上,随即于梁端端模处依前在钢腱上标示之基线,量取其伸长量,以其与事先由拉力与应变曲线上计算所得的伸长量相印证,如两者无误或极为接近时,应即视属为恰当,倘未达预定伸长量时,应再施加拉力,直至达到钢腱有足够的伸长量时为止(所施拉力已达计算所需而其伸长量未达预定长度的原因,是因钢腱伸长时可能遭遇若干装置摩擦而产生拉力损耗之故)。至此,则即认定钢腱上承受的拉力已达预先计算的所需,应即完全停止施拉。如施拉端使用抓握器,应即将锥型梢全力推挤至套筒中空之内,以至完全将钢腱锁紧为止,一般多于千斤顶上装设推挤装置,在施拉的同时自动推挤。如是铆钉头松懈时,则铆钉头即因施拉而自动锁紧于钢钣之上。待抓握器完全锁紧后,始可松脱施拉器,完成施拉作业。此时的钢腱即在两端抓握器锁固下,维持施拉时的拉力。 2100433B
钢腱伸长量指每根钢腱在预应力的作用下的伸长量。在工程上,必须预先计算知道钢腱的伸长量。伸长量的计算分为两种情况:不考虑摩擦力和考虑摩擦力。
不考虑沿钢腱的摩擦损失
若钢腱均均一应力
在预力超过该纲腱比例限值时。上式就不可应用,需另参考应力-应变图,求出
在钢腱施预拉以前。常有若干定量的松弛。如用填隙版的Prescon系统,常计算填隙片长度此松弛必需酌减。再者可能要扣除干缩于在预拉时混凝土的弹性缩短。故填隙片的长度,必等于纲腱的弹性伸长,再加钢腱内的松弛量,以及预力转移时的混凝土缩短。相反,钢腱的弹性伸长量,必由外表伸畏量(apparent elongation),减去初始松弛(initial slack)以及混凝士的弹性缩短而得。
此钢腱内的松弛量极不易准确决定。因此,通常给出初始拉力
伸长量=
例题:
一Prescon纲索18.3m长(见图1),在一端预拉,其初始预力,刚在预力转移时,达到1035MPa。假定在钢索内并无松弛。在预力转移时混凝土干缩为0.0002。并在混凝土中的平均压缩沿钢腱全长为5.5MPa。用
解:
钢材的弹性伸长量为:
填隙片的长度为:
考虑沿钢腱上的摩擦损失
具一定半径R的一根弯曲钢腱,在离开千斤顶端某距离的骷点上,其应力为:
钢腱全长L上的全拉伸量为:
例题:
一钢腱24.4 m长,若沿该圆形曲线上施预拉(图2),R为31m。1240MPa的单位预应力经由千斤顶端施加,并获得其总伸长量为122mm。已知
解:
近似法钢腱中平均应力为:
正确解法给出
- 相关百科
- 相关知识
- 相关专栏
- 直线[运动]轴承
- 直脉榕系
- 直茎红景天
- 直行温度
- 直行程阀
- 直行车道
- 直角梯形
- 直读光谱分析仪
- 直读式数字传感器
- 直读式橡胶密度计技术条件
- 直连路由
- 直驱风力发电系统
- 直齿三面刃铣刀
- 直齿及斜齿锥齿轮基本齿廓
- 直齿条
- 直齿锥齿轮刨齿机第2部分:精度检验
- 基于压电堆驱动器的喷嘴挡板式气体控制阀
- 磷铵技术改造五大磷肥工程的建议
- 以大豆油多元醇制备的硬质聚氨酯泡沫塑料的性能
- 逆变TIG焊机接触引弧电路的设计(引弧电路)
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 引嫩工程扩建区土壤水盐动态与防治土壤盐碱措施
- 中国工程图学学会成立工程与制造系统集成化分会
- 可替代现有隔热保温材料的新型材料
- 以贯穿项目为核心载体的建筑工程技术专业素材库建设
- 多逆变器太阳能光伏并网发电系统的组群控制方法
- 影响萘高效减水剂与普通硅酸盐水泥适应性的关键因素
- 在全县非煤矿山和危化企业安全生产工作会议上的讲话
- 中国工程造价咨询业的发展趋势
- 支持并行工程和智能CAPP的制造资源建模技术
- 中共重庆市委重庆市人民政府关于建设平安重庆的决定
- 智能建筑工程报警与电视监控系统前端设备的安装施工
