准等矩点造价信息
准等矩点常见问题
-
1,测量精度不同,视距差视距不同基辅分化差不同。2.使用的仪器不同,2等的是精密水准仪配合铟瓦钢尺,四等普通尺子。3.测量步骤不同,二等后前前后,四等后后前前。2等要用单程双测站或往返侧,四等无要求。...
-
1,测量精度不同,视距差视距不同基辅分化差不同。2.使用的仪器不同,2等的是精密水准仪配合铟瓦钢尺,四等普通尺子。3.测量步骤不同,二等后前前后,四等后后前前。2等要用单程双测站或往返侧,四等无要求。...
-
比如下图:后视2125+1820+2310=6255,前视2450+1980+2280=6710,前视-后视=6710-6255=355mm,也就是第四点比第一点低355mm
准等矩点文献

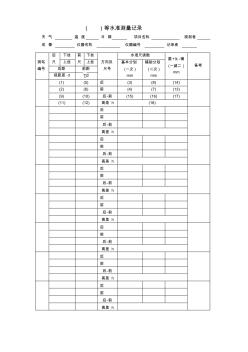 二等四等水准测量记录表
二等四等水准测量记录表
( )等水准测量记录 天 气 温 度 日 期 项目名称 观测者 成 像 仪器名称 仪器编号 记录者 测站 编号 后 尺 下丝 前 尺 下丝 方向及 尺号 水准尺读数 基+ k -辅 (一减二 ) mm 备考 上丝 上丝 基本分划 (一次 ) mm 辅助分划 (二次 ) mm 后距 前距 视距差 d d (1) (5) 后 (3) (8) (14) (2) (6) 前 (4) (7) (13) (9) (10) 后-前 (15) (16) (17) (11) (12) 高差 h (18) 后 前 后-前 高差 h 后 前 后-前 高差 h 后 前 后-前 高差 h 后 前 后-前 高差 h 后 前 后-前 高差 h 后 前 后-前 高差 h 后 前 后-前 高差 h

 忽略水准标尺尺长误差改正的三等水准测量
忽略水准标尺尺长误差改正的三等水准测量
为配合哈尔滨市委确定的南拓战略要求,需在哈南地区提供地形测图和各种工程建设所必需的高程控制点,所以在哈尔滨市二等水准网南侧加密扩充三等水准网。
等价命题1:若A是幂等矩阵,则与A相似的任意矩阵是幂等矩阵;
等价命题2:若A是幂等矩阵,则A的AH,AT,A*,E-AH,E-AT都是幂等矩阵;
等价命题3:若A是幂等矩阵,则对于任意可逆阵T,T^(-1)·A·T也为幂等矩阵;
等价命题4:若A是幂等矩阵,A的k次幂仍是幂等矩阵
(由于数学符号编辑问题,更多等价命题及其证明见扩展阅读1)
由于幂等矩阵所具有的良好性质及其对向量空间的划分,幂等矩阵在可对角化矩阵的分解中具有重要的作用,同时也为空间的投影过程提供了一种工具。
符号说明如下:
AT为矩阵A的转置矩阵;
AH矩阵A的共轭转置矩阵;
A*为矩阵A的伴随矩阵;
E为单位矩阵

幂等矩阵性质
幂等矩阵的主要性质:
1.幂等矩阵的特征值只可能是0,1;
2.幂等矩阵可对角化;
3.幂等矩阵的迹等于幂等矩阵的秩,即tr(A)=rank(A);
4.可逆的幂等矩阵为E;
5.方阵零矩阵和单位矩阵都是幂等矩阵;
6.幂等矩阵A满足:A(E-A)=(E-A)A=0;
7.幂等矩阵A:Ax=x的充要条件是x∈R(A);
8.A的核N(A)等于(E-A)的列空间R(E-A),且N(E-A)=R(A)。 考虑幂等矩阵运算后仍为幂等矩阵的要求,可以给出幂等矩阵的运算:
1)设 A1,A2都是幂等矩阵,则(A1+A2) 为幂等矩阵的充分必要条件为:A1·A2 =A2·A1 = 0,
且有:R(A1+A2) =R (A1) ⊕R (A2);N(A1+A2) =N (A1)∩N(A2);
2)设 A1, A2都是幂等矩阵,则(A1-A2) 为幂等矩阵的充分必要条件为:A1·A2 =A2·A1=A2
且有:R(A1-A2) =R(A1)∩N (A2 );N (A1 - A2 ) =N (A1 )⊕R (A2 );
3)设 A1,A2都是幂等矩阵,若A1·A2 =A2·A1,则A1·A2 为幂等矩阵, 且有:R (A1·A2 ) =R (A1 ) ∩R (A2 );N (A
1·A2 ) =N (A1 ) +N (A2 )。
2009年5月6日,《国家三、四等水准测量规范》发布。
2009年10月1日,《国家三、四等水准测量规范》实施。
- 相关百科
- 相关知识
- 相关专栏
- 双耳活环金瓶松树花卉景
- 马槽桥
- 超正方体
- 恒日光电
- 气动卧式液压千斤顶
- 电动千斤顶
- 卧式千斤顶
- 台座式千斤顶
- 鸭嘴液压千斤顶
- 气压千斤顶
- 齿条千斤顶
- 多功能液压千斤顶
- 气动千斤顶
- 奥林巴斯FL-300R
- 超高压同步千斤顶
- 分离式液压千斤顶
- 应用清单招标与经评审的最低投标价法评标的几点思考
- 永春县农田水利设施产权制度改革和运行管护机制试点
- 以信息化建设为切入点 推动“三基”工作全面落实
- 建造师等职业资格证考试
- 椭圆截面螺旋等通道挤压制备超细晶材料的新工艺
- 制药用水系统使用点取样阀门的应用设计和选型论文
- 在工程建设管理中进行工程造价全过程控制的几点建议
- 中高职衔接道路桥梁工程技术专业教学标准探索与实践
- 制定机械加工劳动定额切削用量时间标准若干问题
- 基于风险接受准则的建筑工程风险评价和决策方法
- 中华人民共和国水产行业标准玻璃钢渔船建造质量要求
- 以提升安全质量管理水平为目标的施工现场标准化建设
- 中厚板生产线升级改造设备中心线基准的测量方法
- 中国水泥工厂余热发电设计规范国家标准即将出台
- 中国石化工程建设项目生产准备与试车管理探索与实践
- 印刷设备维修工国家职业技能标准终审会