主惯性矩
主惯性矩（principal moment of inertia）是2003年公布的土木工程名词。
主惯性矩基本信息
| 中文名 | 主惯性矩 | 外文名 | principal moment of inertia |
|---|---|---|---|
| 所属学科 | 土木工程 | 公布时间 | 2003年 |
《土木工程名词》第一版。 2100433B
主惯性矩造价信息
2003年，经全国科学技术名词审定委员会审定发布。
主惯性矩常见问题
-
惯性矩I=截面上每一微面积与该面积至每一轴距离平方的乘积的集合。 抵抗矩W=I/Ymax 最常用的就是EI（抗弯抵抗矩）；简单的计算公式为W=bh^2/6(b,h分别为截面的宽与高) 至于面积矩是一个...
-
这么多啊。坐等楼主分解，成四个而四问，赚四个采纳 呵呵，这样大家帮助你来计算吧。偶可以帮助你计算一个。
-
是不是在算精冲力，如果是就是剪切线长乘以材料厚度乘以材料抗剪强度乘以2
主惯性矩文献
截面惯性矩的计算
两构件惯性 中心间距 X(cm) 单位长度重量 G1（kg/m） 截面积S1 （cm2） 惯性矩 I 1(cm 4 ) 单位长度重量 G2（kg/m） 截面积S2 （cm2） 惯性矩 I 2(cm 4 ) 偏心距 X1(cm) 2.75 1.9625 2.5 5.2083 5.8875 7.5 0.15625 2.0625 15 20 200 6666.67 10 100 833.333 5 4.28 51.522 65.024 1207.36 11.775 15 0.45 0.7962 #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! 两构件合二为一后，惯性矩的合并的计算 偏心距 X2 (cm) 合并后惯性 中心的惯性 矩I0(cm 4 ) 0.6875 19.5442375 10 22500 3.483801
截面惯性矩计算
截面的几何性质 15-1(I-8) 试求图示三角形截面对通过顶点 A并平行于底边 BC的 轴的惯性 矩。 解：已知三角形截面对以 BC边为轴的惯性矩是 ，利用平行轴定理，可求得 截面对形心轴 的惯性矩 所以 再次应用平行轴定理，得 返回 15-2(I-9) 试求图示 的半圆形截面对于轴 的惯性矩，其中轴 与半圆 形的底边平行，相距 1 m。 面对其底边的惯性矩是 ，用解：知半圆形截 平行轴定理得截面对形心轴 的惯性矩 再用平行轴定理，得截面对轴 的惯性矩 返回 15-3(I-10) 试求图示组合截面对于形心轴 的惯性矩。 解：由于三圆直径相等，并两两相切。它们的圆心构成一个边长为 的等边三 角形。该等边三角形的形心就是组合截面的形心， 因此下面两个圆的圆心， 到形 心轴 的距离是 上面一个圆的圆心到 轴的距离是 。 利用平行轴定理，得组合截面对 轴的惯性矩如下： 返回 15-4(I-
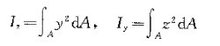
截面惯性矩惯性矩
惯性矩
I=质量X垂直轴二次)the moment of inertia
characterize an object's angular acceleration due to torque.
静矩
静矩(面积X面内轴一次)
把微元面积与各微元至截面上指定轴线距离乘积的积分称为截面的对指定轴的静矩Sx= ydF。
截面惯性矩
截面惯性矩(I=面积X面内轴二次)
截面惯性矩:the area moment of inertia
characterized an object's ability to resist bending and is required to calculate displacement.
截面各微元面积与各微元至截面某一指定轴线距离二次方乘积的积分Ix= y↑2dF。
截面极惯性矩
截面极惯性矩(Ip=面积X垂直轴二次)。
扭转惯性矩
Ip: the torsional moment of inertia
极惯性矩
the polar moment of inertia
截面各微元面积与各微元至垂直于截面的某一指定轴线二次方乘积的积分Ip= P↑2dF。
a quantity to predict an object's ability to resist torsion, to calculate the angular displacement of an object subjected to a torque.
相互关系
截面惯性矩和极惯性矩的关系
截面对任意一对互相垂直轴的惯性矩之和，等于截面对该二轴交点的极惯性矩Ip=Iy+Iz。
翘曲惯性矩Iw：构件在约束条件下，既有翘曲但又并非自由变形，这样截面所承受的约束扭矩部分称为翘曲扭矩。
翘曲惯性矩与抗扭惯性矩共同反映构件抗扭性能的差别。翘曲惯性矩又称翘曲扭转常数，它是截面的一种几何性质，单位mm^6。主要用来计算双力矩作用下截面的翘曲刚度。
2100433B
常见截面的惯性矩公式
矩形
b*h^3/12 其中:b-宽;h-高
三角形
b*h^2/6 其中:b-底长;h-高
圆形
π*d^4/64 其中:d-直径
圆环形
π*D^4*(1-α^4)/64; α=d/D 其中:d-内环直径;D-外环直径
主惯性矩相关推荐
- 相关百科
- 相关知识
- 相关专栏
- 奥创动力传动（深圳）有限公司
- 奥得奥 ADA603
- 主管道坡口机
- 主缸活塞回位弹簧
- 奥古轩
- 奥克斯RC-5080
- 丽原科技（深圳）有限公司
- 丽宫浅水湾
- 丽曼俪全屋智能家居（濮阳）有限责任公司
- 丽标电子科技（上海）有限公司
- 丽水华润燃气有限公司
- 丽水宏远建设有限公司
- 丽水市中兴工程咨询有限公司
- 丽水市大家广告装饰有限公司
- 丽水市大成机械制造有限公司
- 丽水市安居房建设有限公司
- 影响水利工程质量监督职能发挥的主要因素及对策分析
- 张涿高速南水北调干渠特大桥主桥边跨现浇段预压施工
- 主要用固体工业废渣生产硫铝酸盐水泥熟料的方法
- 起重机主梁工字钢磨损及焊接变形的检验案列分析
- 中博会展中心C1区钢结构屋面大型主桁架的施工技术
- 在数控机床上通过监视主轴电机负荷实时监控刀具寿命
- 掌握全局 掌握主动——全球及美国空调市场情况综述
- 医用直线加速器机房升级改造中的主要问题及解决方案
- 影响沥青混凝土路面压实效果的主要因素及采取的对策
- 宜万铁路鲁竹坝2号隧道的主要工程问题及其处理措施
- 云南红河长度982.4主干路210#工程造价指标
- 制约我国工程造价管理体制改革的几个主要问题
- 以数字化设计制造为主线的机电专业卓越工程能力培养
- 状态优化的I~2C总线主控制器的FPGA设计
- 增设Ⅱ型电动轮汽车主发电机磁场电流监测信号的构思
- 以精细化管理为主导的电网工程项目建设质量提升分析
最新词条
安徽省政采项目管理咨询有限公司
数字景枫科技发展（南京）有限公司
怀化市人民政府电子政务管理办公室
河北省高速公路京德临时筹建处
中石化华东石油工程有限公司工程技术分公司
手持无线POS机
广东合正采购招标有限公司
上海城建信息科技有限公司
甘肃鑫禾国际招标有限公司
烧结金属材料
齿轮计量泵
广州采阳招标代理有限公司河源分公司
高铝碳化硅砖
博洛尼智能科技（青岛）有限公司
烧结刚玉砖
深圳市东海国际招标有限公司
搭建香蕉育苗大棚
SF计量单位
福建省中亿通招标咨询有限公司
泛海三江
威海鼠尾草
广东国咨招标有限公司
Excel 数据处理与分析应用大全
甘肃中泰博瑞工程项目管理咨询有限公司
拆边机
山东创盈项目管理有限公司
当代建筑大师
广西北缆电缆有限公司
大山槟榔
上海地铁维护保障有限公司通号分公司
舌花雏菊
甘肃中维国际招标有限公司
华润燃气（上海）有限公司
湖北鑫宇阳光工程咨询有限公司
GB8163标准无缝钢管
中国石油炼化工程建设项目部
韶关市优采招标代理有限公司
莎草目
电梯平层准确度
建设部关于开展城市规划动态监测工作的通知
广州利好来电气有限公司
苏州弘创招投标代理有限公司