最大拉应力理论应用
这一理论适用于脆性材料的断裂破坏,由于计算简单,常被采用。但是,只有脆性材料在某些应力状态下(如二向应力状态下两个主应力均为拉应力;或一个为拉应力,另一个为压应力,且前者的绝对值较后者大),这一理论才与实验结果较为符合 。2100433B
最大拉应力理论造价信息
如用[σ]表示材料单向拉伸时的容许应力,则由该理论建立的强度条件为:
σ1≦[σ]
该理论认为引起材料脆性断裂破坏的因素是最大拉应力。在复杂应力状态下,当一点处的3个主应力中最大的拉应力σ1达到材料在单向拉伸发生断裂破坏的应力时,该点即发生脆性断裂破坏 。
最大拉应力理论应用常见问题
-
钢管是由钢材制成的管子,分有缝钢管和无缝钢管两种。在钢结构设计中,构件和连接等所用钢材在正常工作时容许承受的最大应力值,应小于钢材屈服点而保证一定的强度储备,故等于钢材屈服点除以大于1的安全系数,式中...
-
预应力张拉理论伸长量中钢绞线理论伸长值计算如下:理论伸长值计算公式:△L=Pp×L/(Ap×Ep)理论伸长值计算公式:△L=Pp×L/(Ap×Ep)(其中)Pp=P[(1+e-(KL+μθ))/2]&...
最大拉应力理论是指以拉应力的最大值判断材料是否发生脆性断裂破坏的强度理论,又称第一强度理论。它是在朗肯提出的最大正应力理论的基础上修正得到的。
最大拉应力理论应用文献

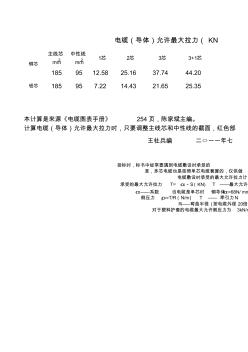 电缆允许最大拉力的计算
电缆允许最大拉力的计算
主线芯 mm2 中性线 mm2 1芯 2芯 3芯 3+1芯 185 95 12.58 25.16 37.74 44.20 铝芯 185 95 7.22 14.43 21.65 25.35 王社兵编 二○一一年七 本计算是来源《电缆图表手册》 254页,陈家斌主编。 计算电缆(导体)允许最大拉力时,只要调整主线芯和中性线的截面,红色部 投标时,标书中经常要遇到电缆敷设时承受的 准,多芯电缆也是按照单芯电缆套算的,仅供做 电缆敷设时承受的最大允许拉力计 承受的最大允许拉力 T= α·S(KN) T ——最大允许 α——系数 当电缆是单芯时 铜导体α=68N/ mm 侧压力 ρ=T/R(N/m) T —— 牵引力N R——弯曲半径 (按电缆外径 20倍 对于塑料护套的电缆最大允许侧压力为 3kN/m 铜芯 电缆(导体)允许最大拉力( KN 4

 螺栓及螺母最大允许拉力表
螺栓及螺母最大允许拉力表
4.8 6.8 8.8 392 588 784 一般构造用钢 机械构造用钢 铬钼合金钢 螺栓M(粗牙螺距) 螺母对边 mm最大拉力( KN) 最大拉力( KN) 最大拉力( KN) 14(×2) 22 44.32 66.47 88.62 16(×2) 24 60.31 90.47 120.62 18(×2.5) 27 73.92 110.9 147.85 20(×2.5) 30 94.32 141.36 188.47 22(×3) 32 117 175.8 234 24(×3) 36 135.7 203.56 271.4 27(×3) 41 177.24 265.88 354.48 30(×3.5) 46 216.1 324.15 432.17 33(×3.5) 50 267.77 398.8 535.4 36(×4) 55 312.8 472.6 630 39(×4) 60 376.5
最大拉应变理论是指以伸长线应变的最大值判断材料是否发生脆性断裂破坏的强度理论,又称第二强度理论。它是在圣维南提出的最大正应变理论的基础上修正得到的。
这一理论通常用于脆性材料的断裂破坏。事实上,只有脆性材料在某些应力状态下,如铸铁管在二向应力状态下,一个主应力为拉应力,其值小于另一个为压应力的绝对值,其试验结果才与按该理论计算的结果接近 。2100433B
弹性失效准则的强度条件为:σ1-σ3≤[σ]。式中σ1和σ3分别为材料在复杂应力状态下的最大主应力和最小主应力;σ1-σ3,也即当量应力;[σ]为材料的许用应力。实验表明,此理论和材料破坏的结果比较吻合,不但能说明塑性材料的流动破坏,还能说明脆性材料的剪断。
- 相关百科
- 相关知识
- 相关专栏
- 最大拉应变理论
- 最大持续功率
- 最大持续坡度
- 最大持续工作电压
- 最大摊铺厚度
- 最大方差旋转法
- 最大时用水量
- 最大有效力矩准则
- 最大水平位移
- 最大法向应力
- 最大滑差转矩
- 最大潮差
- 最大烈度
- 最大热负荷
- 最大爬坡角
- 最大直径定理
- 分形DGS单元结构设计及其在微带电路中的应用
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 云计算技术在城市轨道交通运营指挥管理系统中的应用
- 应对水源突发污染的城市供水应急处理技术与应用
- 有限元法在软土浅埋隧道施工过程的动态模拟中的应用
- 新型基于热力学法的水泵效率数学模型及应用
- 振冲碎石桩地基加固技术在椒江标准海塘工程中的应用
- 应用亚温淬火工艺解决45钢槽型螺母淬裂问题的探索
- 乙烯基树脂混凝土电解槽的性能及在湿法冶金中的应用
- 政府与社会资本合作(PPP)项目审计监督理论
- 应用清单招标与经评审的最低投标价法评标的几点思考
- 智能化技术在电气工程自动化控制中的应用与实践研讨
- 应用型人才培养模式下高校机电工程综合实践改革探索
- 智能电力监控管理系统在某飞机维修公司工程中的应用
- 异形人工挖孔桩和预应力土层锚杆组合在基坑中的应用
- 智能照明系统在高校教学楼建筑节能改造中的应用