转动惯量列表
转动惯量列表基本信息
| 中文名 | 转动惯量列表 | 外文名 | Moment of inertia list |
|---|---|---|---|
| 描 述 | 常见物理模型的转动惯量 | 学 科 | 力学 |
| 领 域 | 力学 | 相关术语 | 截面惯量 |
| 描述 |
转动惯量 |
注解 |
|---|---|---|
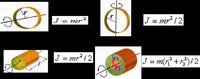
| 两端开通的薄圆柱壳, 半径为r,质量为m |
此表示法假设了壳的厚度可以忽略不计。此为下一个物体,当其r1=r2时的特例。 |
|
| 两端开通的厚圆柱, 内半径r1,外半径r2, 高h,质量m |
或者定义标准化厚度tn=t/r并定义r=r2, 可得 |
— |
| 实心圆柱, 半径为r,高h, 质量m |
此为前面物体,当其r1=0时的特例。 |
|
| 薄圆盘,半径为r, 质量m |
此为前面物体,当其h=0时的特例。 |
|
| 圆环,半径为r, 质量m |
此为后面环面,当其b=0时的特例。 |
|
| 实心球,半径为r, 质量m |
— |
|
| 空心球,半径为r, 质量m |
— |
|
| 圆锥,半径为r,高h, 质量m |
— |
|
| 实心长方体,高h, 宽w,长d,质量m |
边长为 s的立方体的转动惯量 |
|
| 细棒,长L,质量m |
此表示法假设了棒的宽度和厚度可以忽略不计。此为前面物体,当其w=L,h=d=0时的特例。 |
|
| 细棒,长L,质量m |
此表示法假设了棒的宽度和厚度可以忽略不计。 |
|
| 环面,圆管的半径a, 截面的半径b,质量m。 |
关于直径: 关于纵轴: |
— |
| 薄多边形,质量m。 |
— |
转动惯量列表造价信息
-
转动惯量
-
截面惯量列表
-
惯量张量列表
对于一个有多个质点的系统,
值得注意的是,不应将其与截面惯量(又称截面二次轴矩(second axial moment of area),截面矩(area moment of inertia)混淆,后者用于弯折方面的计算。以下之转动惯量假设了整个物体具有均匀的常数密度。
转动惯量列表常见问题
-
J=mr*r (1) F=mg => m=F/g (2) (2)代(1)得: 转动惯量 J
-
不同的电机转动惯量大小不同,我想知道转动惯量大点好还是小点好?如盘式电机转动惯量问题。
回答这个问题,首先要明白转动惯量这个概念,转动惯量也叫惯性矩;构件中各质点或质量单元的质量与其到给定轴线的距离平方乘积的总和。所以,转动惯量大点好还是小点好,要看整个系统的要求了,比如矿山机械中的颚式...
-
刚体绕轴转动惯性的度量。其数值为J=∑ mi*ri^2,式中mi表示刚体的某个质点的质量,ri表示该质点到转轴的垂直距离。;求和号(或积分号)遍及整个刚体。转动惯量只决定于刚体的形状、质量分布和转轴的...
转动惯量列表文献

 GQ40L型钢筋切断机飞轮转动惯量分析
GQ40L型钢筋切断机飞轮转动惯量分析
钢筋切断机在工作行程时,能量的来源主要靠飞轮降速释放出贮存的功能获得。据有关资料介绍,飞轮速度降低10%时,供给的能量为其总能量的19%;降低20%时为36%;降低30%时为51%。由此可见速度降低10%比降低20%其轮出能量少近一半。设计计算时,应力求飞轮速度降尽可能大些,但是,当飞轮速度降低时,电机转速也随着降低,电机工作电流将成比例增加,促使电机工作情况恶化。因此,飞轮转速降(即不均匀系数δ)的取值,受到电机性能(即过载条件和发热条件)的限制。

 转动惯量对水电机组动态性能的影响
转动惯量对水电机组动态性能的影响
研究了GD2对水电机组动态性能的影响.结果表明,GD2的减小对并列运行的水轮发电机组的静态稳定是有利的,对孤立运行的水轮机调节系统的稳定是不利的,但可以通过改善调速器参数整定来弥补.随着GD2的减小,水轮机组动态品质的满足与否取决于转速最大偏差Δxmax.
极转动惯量就是薄的圆盘相对于中心轴线的转动惯量。
转动惯量简介
转动惯量(Moment of Inertia)是刚体转动时惯性的量度,其量值取决于物体的形状、质量分布及转轴的位置。刚体的转动惯量有着重要的物理意义,在科学实验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。 电磁系仪表的指示系统,因线圈的转动惯量不同,可分别用于测量微小电流(检流计)或电量(冲击电流计)。在发动机叶片、飞轮、陀螺以及人造卫星的外形设计上,精确地测定转动惯量,都是十分必要的。
对于质量分布均匀,外形不复杂的物体可以从它的外形尺寸的质量分布用公式计算出相对于某一确定转轴的转动惯量。对于几何形状简单、质量分布均匀的刚体可以直接用公式计算出它相对于某一确定转轴的转动惯量。而对于外形复杂和质量分布不均匀的物体只能通过实验的方法来精确地测定物体的转动惯量,因而实验方法就显得更为重要。
Moment of Inertia刚体绕轴转动惯性的度量。其数值为J=∑ mi*ri^2,式中mi表示刚体的某个质点的质量,ri表示该质点到转轴的垂直距离。
求和号(或积分号)遍及整个刚体。转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。形状规则的均质刚体,其转动惯量可直接计得。不规则刚体或非均质刚体的转动惯量,一般用实验法测定。转动惯量应用于刚体各种运动的动力学计算中。
描述刚体绕互相平行诸转轴的转动惯量之间的关系,有如下的平行轴定理:刚体对一轴的转动惯量,等于该刚体对同此轴平行并通过质心之轴的转动惯量加上该刚体的质量同两轴间距离平方的乘积。由于和式的第二项恒大于零,因此刚体绕过质量中心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。
精确定义
转动惯量严格来说是一个张量,必须从张量的角度对其进行定义。出于简单的角度考虑,这里仅给出绕质心的转动惯量张量的定义及其在力矩方程中的表达.
设有一个刚体A,其质心为C,刚体A绕其质心C的转动惯量张量定义为Jc,则Jc=∫ρ(r●rδ-rr)dV。该积分遍及整个刚体A,且,
其中,r=r1 e_1 + r2 e_2 + r3 e_3 ,是刚体质心C到刚体上任一点B的矢径;表达式rr是两个矢量的并乘;而单位张量δ是度量张量,δ=δ_ij e_i e_j ,这里i和j是哑指标,标架(C;e_1,e_2,e_3)是一个典型的单位正交曲线标架;ρ是刚体的密度。
转动惯量张量的力矩方程
设刚体A所受到的绕其质心C的合力矩矢量为ΣMc,刚体A在惯性系下的角速度矢量为ω,角加速度矢量为α,A绕其质心的转动惯量张量为Jc,则有如下的力矩方程:
ΣMc=Jc●α+ω×Jc●ω
将上面的矢量形式的力矩方程向各个坐标轴投影(或者,更确切地说,与各个坐标轴的单位方向矢量相点乘),就可以获得各个坐标轴分量方向的标量形式的力矩方程。
转动惯量张量Jc是一个二阶张量,虽然在标架(C;e_1,e_2,e_3)下它有九个分量,但是因为它是一个对称张量,故其实际独立的分量只有六个。
转动惯量定义为:J=∑ mi*ri^2 (1)式中mi表示刚体的某个质点的质量,ri表示该质点到转轴的垂直距离。
转动惯量是表征刚体转动惯性大小的物理量,它与刚体的质量、质量相对于转轴的分布有关。
刚体的转动惯量是由质量、质量分布、转轴位置三个因素决定的。 (2) 同一刚体对不同转轴的转动不同,凡是提到转动惯量,必须指明它是对哪个轴的才有意义。
- 相关百科
- 相关知识
- 相关专栏
- 转动机械的转子动力学设计
- 转动钢管气割
- 转变温度
- 转向油泵
- 转向油泵可靠性试验台
- 转向节锻造线切边机干油润滑泵补油装置
- 转型中的传媒:宁波日报报业集团的实践与思考
- 转子的动平衡
- 转子齿数
- 转差率
- 转底炉法含铁尘泥金属化球团
- 转底炉法粗锌粉
- 转底炉炼铁
- 转底炉直接还原复合球团工艺及理论
- 转换时间
- 转炉和电炉用透气砖
- 太阳能热水工程竣工验收报告标准一系列表格全套报告
- 太阳能热水工程竣工验收资料实用标准一系列表格全套
- 爆破安全规程爆破工程分级管理列表
- 地产企业管理之全国房地产行业基准职位列表及职位说明
- 城西施工组织主要施工机械设备配备方案及设备列表
- SH3405-2017钢制管道壁厚列表
- 工程验收规范文章列表厕浴间工程验收规范
- 工程验收规范文章列表
- 工程中间验收交接记录建筑工程竣工验收系列表格
- 国际制冷学会关于制冷领域应优先问题列表
- 广州市财政项目结算评审资料要求一般性列表格式
- 工程验收规范文章列表之九玻璃工程验收规范
- 工程验收规范文章列表之四门窗工程验收规范
- 广东各地LED道路照明招投中标信息列表
- 中国五大发电公司及所属电厂列表及分部收集资料
- 安徽省建造师协会施工全过程资料详细列表汇总