圆周角定理
圆周角定理指的是一条弧所对圆周角等于它所对圆心角的一半。这一定理叫做圆周角定理。该定理反映的是圆周角与圆心角的关系。
圆周角定理基本信息
| 中文名称 | 圆周角定理 | 外文名称 | The circumferential angle theorem |
|---|---|---|---|
| 应用学科 | 数学 | 适用领域范围 | 平面几何 |
圆周角定理定理证明
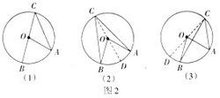
已知在⊙O中,∠BOC与圆周角∠BAC同对弧BC,求证:∠BOC=2∠BAC.
证明:
情况1:
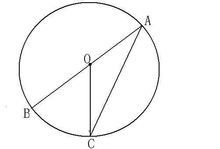
如图1,当圆心O在∠BAC的一边上时,即A、O、B在同一直线上时:
∵OA、OC是半径
解:∴OA=OC
∴∠BAC=∠ACO(等边对等角)
∵∠BOC是△AOC的外角
∴∠BOC=∠BAC+∠ACO=2∠BAC
情况2:
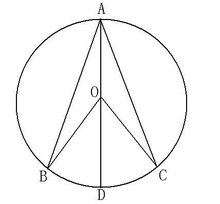
如图2,,当圆心O在∠BAC的内部时:
连接AO,并延长AO交⊙O于D ∵OA、OB、OC是半径
解:∴OA=OB=OC
∴∠BAD=∠ABO,∠CAD=∠ACO(等边对等角)
∵∠BOD、∠COD分别是△AOB、△AOC的外角
∴∠BOD=∠BAD+∠ABO=2∠BAD(三角形的外角等于两个不相邻两个内角的和)
∠COD=∠CAD+∠ACO=2∠CAD(三角形的外角等于两个不相邻两个内角的和)
∴∠BOC=∠BOD+∠COD=2(∠BAD+∠CAD)=2∠BAC
情况3:
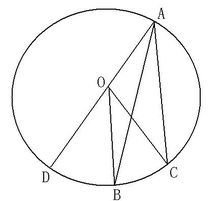
如图3,当圆心O在∠BAC的外部时: 连接AO,并延长AO交⊙O于D连接OA,OB。
解:∵OA、OB、OC、是半径
∴OA=OB=OC
∴∠BAD=∠ABO(等腰三角形底角相等),∠CAD=∠ACO(OA=OC)
∵∠DOB、∠DOC分别是△AOB、△AOC的外角
∴∠DOB=∠BAD+∠ABO=2∠BAD(三角形的外角等于两个不相邻两个内角的和)
∠DOC=∠CAD+∠ACO=2∠CAD(三角形的外角等于两个不相邻两个内角的和)
∴∠BOC=∠DOC-∠DOB=2(∠CAD-∠BAD)=2∠BAC
圆心角等于180度的情况呢?
看情况1的图,圆心角∠AOB=180度,圆周角是∠ACB,
显然因为∠OCA=∠OAC=∠BOC/2
∠OCB=∠OBC=∠AOC/2
所以∠OCA+∠OCB=(∠BOC+∠ABC)/2=90度
所以2∠ACB=∠AOC
圆心角大于180度的情况呢?
看情况3的图,圆心角是(360度-∠AOB),圆周角是∠ACB,
只要延长CO交园于点E,由圆心角等于180度的情况可知∠CAE=∠CBE=90度
所以∠ACB+∠AEB=180度,即∠ACB=180度-∠AEB
由情况2可知:∠AOB=2∠AEB
所以360度-∠AOB=2(180度-∠AEB)=2∠ACB
圆周角定理造价信息
圆周角定理定理推论
1.一条弧所对的圆周角等于它所对的圆心角的一半;
2.圆周角的度数等于它所对的弧度数的一半;
3.在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等。
4.半圆(直径)所对的圆周角是直角。
5.90°的圆周角所对的弦是直径。
注意:在圆中,同一条弦所对的圆周角有无数个。
圆周角的度数等于它所对弧上的圆心角度数的一半。
圆周角定理常见问题
-
没有圆切角定理,只有弦切角定理:弦切角等于它所夹的弧对的圆周角
-
首先更正一下,是弦切角,老沈瞎说呢。你把图画出来,AB是圆O切线,AC是弦。做过切点A的直径,交圆O于A、D。连接B、D。证明:因为AD是圆O直径,AB是圆O切线所以∠C=90°=∠BAD所以∠BAC...
-
圆的切线长定理是什么?圆的切线长定理是从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线,平分两条切线的夹角。
圆周角定理文献

 墙角梯子下滑问题及勾股定理
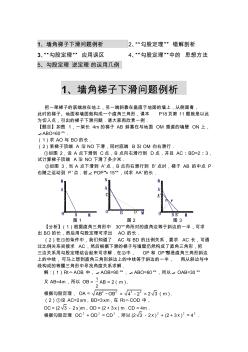
墙角梯子下滑问题及勾股定理
1、墙角梯子下滑问题例析 2、“勾股定理” 错解剖析 3、“勾股定理” 应用误区 4、“勾股定理”中的 思想方法 5、勾股定理 逆定理 的运用几例 1、墙角梯子下滑问题例析 把一架梯子的底端放在地上,另一端斜靠在垂直于地面的墙上,从侧面看, 此时的梯子、地面和墙面就构成一个直角三角形,课本 P18页第 11题就是以此 为切入点,引出的梯子下滑问题.请大家再欣赏一例. 【题目】如图 1,一架长 4m的梯子 AB 斜靠在与地面 OM 垂直的墙壁 ON 上, ∠ABO=60°. (1)求 AO 与 BO的长. (2)若梯子顶端 A 沿 NO 下滑,同时底端 B 沿 OM 向右滑行. ①如图 2,设 A 点下滑到 C点,B 点向右滑行到 D点,并且 AC∶BD=2∶3, 试计算梯子顶端 A 沿 NO 下滑了多少米. ②如图 3,当 A 点下滑到 'A 点,B点向右滑行到 'B 点时,梯子 AB 的
圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。证明:
情况一:先考虑一种特殊情况——圆心O在圆周角∠BAC的边上(如图一).由三角形外角性质有
但
情况二:如果圆心O在圆周角∠BAC的内部(如图二),可以划归为前一种类型——引直径AD。∠BAD,∠CAD都是圆心在边上的圆周角。则有:
两式相加即得
.情况三:如果圆心O在圆周角∠BAC的外部(如图三),仍可以 划归为前一种类型——引直径AD。这时∠BAD,∠CAD都是圆心在边上的圆周角。则有:
两式相减即得
这样,即完成了定理的证明。圆周角定理有如下推论:
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.联系圆心角、弧、弦、弦心距之间的关系.对于在推理论证及相关计算中有着广泛的用途.
推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。这两个推论是判定直角或直角三角形的又一依据,为在圆中确定直角,构造垂直关系,创造了条件,因此它是圆中一个很重要的性质。

割线定理验证推导
证明一
已知:如图直线ABP和CDP是自点P引的⊙O的两条割线
求证:PA·PB=PC·PD
证明:连接AD、BC∵∠A和∠C都对弧BD
∴由圆周角定理,得 ∠DAP=∠BCP
又∵∠P=∠P
∴△ADP∽△CBP (如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。)
∴AP:CP=DP:BP
即AP·BP=CP·DP
证明二
既然圆内接四边形定理可以从割线定理而得,那么或许割线定理就可以从圆内接四边形定理而得。
如图所示。
已知:从圆O外一点P引两条圆的割线,一条交圆于A、B,另一条交圆于C、D
求证:AP·BP=CP·DP
证明:连接AC、BD
由圆内接四边形定理得
∠ABD+∠DCA=∠CAB+∠BDC=180°
又∵∠ACP+∠DCA=∠DCP=180°,∠CAP+∠CAB=∠BAP=180°(平角的定义)
∴∠ABD=∠ACP,∠BDC=∠CAP(同角的补角相等)
∴△ACP∽△DBP(两角对应相等的三角形相似)
∴AP/DP=CP/BP(相似三角形对应边成比例)
∴AP·BP=CP·DP(比例基本性质)
证明三
根据切割线定理求证。
已知:从圆O外一点P引两条圆的割线,一条交圆于A、B,另一条交圆于C、D
求证:AP·BP=CP·DP
过点P作圆O的切线,记切点为T
由切割线定理可知:AP·BP=PT²,CP·DP=PT²
∴AP·BP=CP·DP
- 相关百科
- 相关知识
- 相关专栏
- 6-羧基吡啶-2-甲醇
- 沸石催化与分离技术
- (2-氯-3-喹啉)甲醇
- YF-PD 系列工业控制柜
- 沸石分子筛
- 铯沸石
- 沸石矿
- 4a沸石
- 1H-吡唑-4-甲醇
- 1-(氨基甲基)环丁烷甲醇
- (四氢吡喃-3-基)甲醇
- 沸石催化裂化催化剂
- (手动)平衡阀
- 3-环己基-1,1-二甲醇
- 微孔沸石储氢理论与模拟
- 缙云沸石的开发应用
- 信贷扩张、房地产价格波动与银行稳定理论及其经验分析
- 合力矩定理在土建工程中的应用
- 对新火电厂大气污染物排放标准脱硫规定理解
- Hermite插值神经网络权值和结构确定理论
- 受施工扰动影响土体环境稳定理论与变形控制
- 稳定理论的低碳钢托架结构参数的优化设计
- 可变模糊集对立统一定理的水安全评价
- 数值分析课程中定理反讲教学方式
- 压力容器金属材料进厂验收最新规定理解
- 不确定理论的电力系统脆弱性评估
- 压差旁通阀压差值再设定理论计算
- 岩体等效强度参数确定理论和方法
- 基于压电堆驱动器的喷嘴挡板式气体控制阀
- 电气工程及其自动化特色专业建设探索
- 分形DGS单元结构设计及其在微带电路中的应用
- 磷铵技术改造五大磷肥工程的建议