圆周角
圆周角基本信息
| 中文名 | 圆周角 | 外文名 | angle in a circular segment |
|---|---|---|---|
| 定 义 | 顶点在圆上且两边都和圆相交的角 | 特 点 | 顶点在圆上,两边为圆的两条弦 |
| 相关定理 | 圆周角定理 | 学 科 | 数学 |
圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。证明:
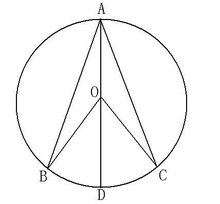
情况一:先考虑一种特殊情况——圆心O在圆周角∠BAC的边上(如图一).由三角形外角性质有
但
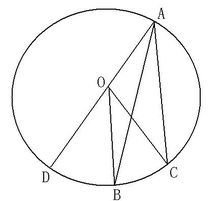
情况二:如果圆心O在圆周角∠BAC的内部(如图二),可以划归为前一种类型——引直径AD。∠BAD,∠CAD都是圆心在边上的圆周角。则有:
两式相加即得
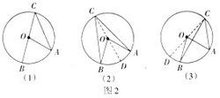
.情况三:如果圆心O在圆周角∠BAC的外部(如图三),仍可以 划归为前一种类型——引直径AD。这时∠BAD,∠CAD都是圆心在边上的圆周角。则有:
两式相减即得
这样,即完成了定理的证明。圆周角定理有如下推论:
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.联系圆心角、弧、弦、弦心距之间的关系.对于在推理论证及相关计算中有着广泛的用途.
推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。这两个推论是判定直角或直角三角形的又一依据,为在圆中确定直角,构造垂直关系,创造了条件,因此它是圆中一个很重要的性质。
圆周角造价信息
命题1: 在圆中作弦MN,于直线MN同侧取点A、B、C,使点A、B、C分别在圆内、上、外,将点A、B、C分别与点M、N连结,则有∠A>∠B>∠C。
命题2: 顶点在圆外的角(两边与圆相交)的度数等于其所截两弧度数差的一半;顶点在圆内的角(两边与圆相交)的度数等于其及其对顶角所截弧度数和的一半。
证明:如图,过C作CE//AB,交圆于E,(如图四)
则有∠P=∠DCE,弧AC=弧BE(圆中两平行弦所夹弧相等)
而∠DCE的度数等于弧DE的一半,弧DE=弧BD-弧BE=弧BD-弧AC
所以∠DCE的度数等于“弧BD-弧AC”的一半
即“顶点在圆外的角(两边与圆相交)的度数等于其所截两弧度数差的一半”
另外也可以连接BC,则∠P=∠BCD-∠B
∠BCD的度数等于弧BD的度数的一半
∠B的度数等于弧AC的度数的一半
同样得“顶点在圆外的角(两边与圆相交)的度数等于其所截两弧度数差的一半”
圆内角的证明完全类似:
过C作CE//AB,交圆于E,
则有∠APC=∠C,弧AC=弧BE(圆中两平行弦所夹弧相等)
而∠C的度数等于弧DE的一半,
弧DE=弧BD 弧BE=弧BD 弧AC
所以∠APC的度数等于“弧BD 弧AC”的一半
即“顶点在圆内的角(两边与圆相交)的度数等于其所截两弧度数和的一半”
另外也可以连接BC进行证明
圆周角(angle of circumference)是指顶点在圆上,且两边和圆相交的角。在同圆或等圆中,两圆周角相等,则其所对的弦(或弧)也相等;反之,等弧所对的圆周角相等。而等弦所对圆周角相等或相补,圆周角的度数等于它所对弧的度数的一半。
对于一个圆周角,角的内部必然夹了一段圆弧,通常把圆周角说成是这一弧上的圆周角,或说这一弧所对的圆周角。另外,角的外部也有一段圆弧,我们还把圆周角说成是这一弧所含的圆周角。
圆周角常见问题
-
在CAD中计算椭圆周长参考如下步骤:1、单击椭圆绘制命令,绘制椭圆。2、绘成椭圆如图:3、鼠标左键单击椭圆轮廓,选中椭圆:4、选中椭圆轮廓的基础上,在CAD页面左下角命令栏输入命令“Li”5、求出椭圆...
-
输入aa,然后回车,继续输入o,选择椭圆,,面积和周长全部出来
-
1.型号:RMT 2. 适于不同领域的多种混匀工作,温和的振动,适合培养皿和锥形瓶3. 可调振荡速度:50-300rpm4. &...
圆周角文献

 含圆周非贯穿裂纹悬臂管道的振动分析与裂纹识别
含圆周非贯穿裂纹悬臂管道的振动分析与裂纹识别
根据线性断裂力学理论和应变能释放原理,推导了含圆周非贯穿裂纹管道在轴力、剪力和弯矩等荷载作用下的局部柔度系数方程,利用适应性S impson方法编写了数值积分程序进行局部柔度系数求解,建立了含裂纹管道的二维有限元模型进行含裂纹悬臂管道的振动特性分析,应用等值线图原理进行了悬臂管道的裂纹识别。研究结果表明:裂纹模型克服了当前裂纹模型仅针对特定的荷载模式或非空心截面的缺陷,基于等值线图法能有效识别含裂纹悬臂管道的裂纹位置、深度。

 ZGCr4铸钢支承辊辊颈圆周裂纹检验分析
ZGCr4铸钢支承辊辊颈圆周裂纹检验分析
运用化学分析、光学显微镜和扫描电镜等检测手段,对裂纹的形成和开裂特征进行了系统的金相分析。结果表明,辊颈圆周出现裂纹的主要原因是辊颈凹槽处碳、磷含量严重超标、中心碳偏析、沿晶分布的共晶碳化物和一次碳化物以及显微孔隙等因素致使晶界严重薄弱脆化,造成在铸钢支承辊最终热处理的冷却过程中开裂。
圆周角定理定理推论
1.一条弧所对的圆周角等于它所对的圆心角的一半;
2.圆周角的度数等于它所对的弧度数的一半;
3.在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等。
4.半圆(直径)所对的圆周角是直角。
5.90°的圆周角所对的弦是直径。
注意:在圆中,同一条弦所对的圆周角有无数个。
圆周角的度数等于它所对弧上的圆心角度数的一半。
圆周角定理定理证明
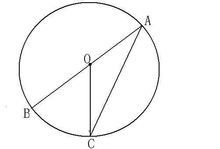
已知在⊙O中,∠BOC与圆周角∠BAC同对弧BC,求证:∠BOC=2∠BAC.
证明:
情况1:
如图1,当圆心O在∠BAC的一边上时,即A、O、B在同一直线上时:
∵OA、OC是半径
解:∴OA=OC
∴∠BAC=∠ACO(等边对等角)
∵∠BOC是△AOC的外角
∴∠BOC=∠BAC+∠ACO=2∠BAC
情况2:
如图2,,当圆心O在∠BAC的内部时:
连接AO,并延长AO交⊙O于D ∵OA、OB、OC是半径
解:∴OA=OB=OC
∴∠BAD=∠ABO,∠CAD=∠ACO(等边对等角)
∵∠BOD、∠COD分别是△AOB、△AOC的外角
∴∠BOD=∠BAD+∠ABO=2∠BAD(三角形的外角等于两个不相邻两个内角的和)
∠COD=∠CAD+∠ACO=2∠CAD(三角形的外角等于两个不相邻两个内角的和)
∴∠BOC=∠BOD+∠COD=2(∠BAD+∠CAD)=2∠BAC
情况3:
如图3,当圆心O在∠BAC的外部时: 连接AO,并延长AO交⊙O于D连接OA,OB。
解:∵OA、OB、OC、是半径
∴OA=OB=OC
∴∠BAD=∠ABO(等腰三角形底角相等),∠CAD=∠ACO(OA=OC)
∵∠DOB、∠DOC分别是△AOB、△AOC的外角
∴∠DOB=∠BAD+∠ABO=2∠BAD(三角形的外角等于两个不相邻两个内角的和)
∠DOC=∠CAD+∠ACO=2∠CAD(三角形的外角等于两个不相邻两个内角的和)
∴∠BOC=∠DOC-∠DOB=2(∠CAD-∠BAD)=2∠BAC
圆心角等于180度的情况呢?
看情况1的图,圆心角∠AOB=180度,圆周角是∠ACB,
显然因为∠OCA=∠OAC=∠BOC/2
∠OCB=∠OBC=∠AOC/2
所以∠OCA+∠OCB=(∠BOC+∠ABC)/2=90度
所以2∠ACB=∠AOC
圆心角大于180度的情况呢?
看情况3的图,圆心角是(360度-∠AOB),圆周角是∠ACB,
只要延长CO交园于点E,由圆心角等于180度的情况可知∠CAE=∠CBE=90度
所以∠ACB+∠AEB=180度,即∠ACB=180度-∠AEB
由情况2可知:∠AOB=2∠AEB
所以360度-∠AOB=2(180度-∠AEB)=2∠ACB
- 相关百科
- 相关知识
- 相关专栏
- 圆形煤窑
- 圆条棉藓
- 圆柏九龙山群体
- 圆柏海南个体
- 圆柏海南个体001
- 圆柏绩溪古4号
- 圆柏绩溪古5号
- 圆柏群体
- 圆柱与圆锥
- 圆柱凸轮
- 圆柱分度凸轮机构
- 圆柱形筒管扁丝用筒管的尺寸、偏差和标记
- 圆柱滚子抗振耐高温轴承
- 圆柱锁
- 圆柱锂电池
- 圆环链爬车机
- 基于压电堆驱动器的喷嘴挡板式气体控制阀
- 电气工程及其自动化特色专业建设探索
- 分形DGS单元结构设计及其在微带电路中的应用
- 磷铵技术改造五大磷肥工程的建议
- 以大豆油多元醇制备的硬质聚氨酯泡沫塑料的性能
- 逆变TIG焊机接触引弧电路的设计(引弧电路)
- 预制砌块(砖、石)挡土墙工程砌体施工安全技术交底
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 引嫩工程扩建区土壤水盐动态与防治土壤盐碱措施
- 中华华丹雨、污水管道沟槽开挖专项施工方案教学教材
- 中国工程图学学会成立工程与制造系统集成化分会
- 中国吹制玻璃行业市场前景分析预测年度报告(目录)
- 可替代现有隔热保温材料的新型材料
- 医院病房楼工程施工装饰装修工程施工控制
- 在生活中构筑自然——河南天旺园林工程有限公司剪影
- 中国机械工程学会授予材料热处理工程师资格人员名单