应力状态边界条件
应力状态应力边界条件
应力边界条件即弹性体在外力作用下处于平衡状态的条件,是物体内部的各点的应力分量应满足平衡方程式,物体边界上各点也必须是平衡的。
由后者将导出应力边界条件。换言之,所谓应力边界条件就是在给定面力的边界上应力分量与面力分量之间的关系。
应力状态混合边界条件
混合边界条件有两种情况,一种情况是在物体的整个边界s上,一部分为已知应力,即给定应力的边界s ;另一种情况是在同一部分边界上已知部分位移和部分应力,即给定位移与应力混合边界条件。
应力状态造价信息
可以证明,无论一点处的应力状态如何复杂,最终都可用剪应力为零的三对相互垂直面上的正应力,即主应力表示。
应力状态三向应力状态
当三个正应力均不为零时,称该点处于三向应力状态。若只有两对面上的主应力不等于零,则称为二向应力状态或平面应力状态。若只有一对面上的主应力不为零,则称为单向应力状态。
应力状态应力圆
应力圆是分析应力状态的图解法。
在已知一点处相互垂直的待定截面上应力的情况下,通过应力圆可求得该点处其他截面上的应力。应力圆也称莫尔圆。
在变形体内原子被迫偏离平衡位置,则该物体便出现应力。所谓应力状态就是物体内的原子被迫偏离其平衡位置的状态。物体内各点产生屈服或断裂都和该点所受的应力状态有关。为了定性说明变形体内某点的应力状态,常采用主应力状态图示(简称应力图示)。
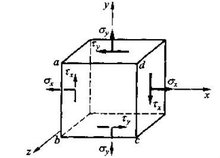
应力状态(stress state),物体受力作用时,其内部应力的大小和方向不仅随截面的方位而变化,而且在同一截面上的各点处也不一定相同。通过物体内一点可以作出无数个不同取向的截面,其中一定可以选出三个互相垂直的截面,在它上面只有正应力作用,剪应力等于零,用这三个截面表达的某点上的应力,即称为此点的应力状态。
三个主应力不等且都不等于零的应力状态称为三轴(三维、空间)应力状态;如有一个主应力等于零,则称为双轴(二维、平面)应力状态;如有两个主应力等于零则称为单轴(或单向)应力状态。
构件在受力时将同时产生应力与应变。构件内的应力不仅与点的位置有关,而且与截面的方位有关,应力状态理论是研究指定点处的方位不同截面上的应力之间的关系。应变状态理论则研究指定点处的不同方向的应变之间的关系。应力状态理论是强度计算的基础,而应变状态理论是实验分析的基础。
如果已经确定了一点的三个相互垂直面上的应力,则该点处的应力状态即完全确定。因此在表达一点处的应力状态时,为方便起见,常将“点”视为边长为无穷小的正六面体,即所谓单元体,并且认为其各面上的应力均匀分布,平行面上的应力相等。
应力状态边界条件常见问题
-
假定粱在XY平面内,粱沿X方向放置,左边固定饺支座,右边滑动饺支座,那么边界为:左边(u1=0,u2=0),右边(u2=0),如果是平面粱,还应限制整根粱Z向位移,以及粱绕X轴的转动。
在外力作用下,物体的变形通常可分为体积改变和形状改变两种成分,并且认为,体积的改变是由于各向相等的应力引起的。
实验表明,同体材料在各向相等的应力作用下,一般都表现为弹性性质。因而可以认为材料的塑性变形主要是物体产生形状变化时产生的。
所谓应力球张量 是一种平均的等向应力状态(三向等拉或等压),对各向同性材料,它引起微元体积膨胀或收缩。应力偏量表示实际应力状态对其平均应力状态的偏离,它引起微元形状的改变。
应力状态边界条件文献

 钢管玻璃润滑热挤压工艺的边界条件
钢管玻璃润滑热挤压工艺的边界条件
以P91钢为例进行了小口径钢管玻璃润滑热挤压工艺试验,记录不同挤压温度、挤压速度下的挤压力变化。以物理试验的观察结果为依据,借助于有限元软件DEFORM 2D进行模拟分析,根据稳定挤压阶段的挤压力大小,得出相应的摩擦系数,根据挤压力曲线的后期变化趋势,得出相应的换热系数。并最终得出玻璃润滑边界的换热系数q≤1.0×103J/(m2.s.℃),库仑摩擦系数μ=0.02~0.03,从而为钢管玻璃润滑热挤压工艺提供合理准确的边界参数。

 典型造价设计边界条件(V1.0版)
典型造价设计边界条件(V1.0版)
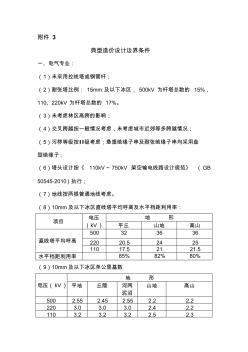
附件 3 典型造价设计边界条件 一、电气专业: (1)未采用拉线塔或钢管杆; (2)耐张塔比例: 15mm 及以下冰区, 500kV 为杆塔总数的 15%, 110、220kV 为杆塔总数的 17%。 (3)未考虑林区高跨的影响; (4)交叉跨越按一般情况考虑,未考虑城市近郊等多跨越情况; (5)污秽等级按Ⅱ级考虑;悬垂绝缘子串及耐张绝缘子串均采用盘 型绝缘子; (6)塔头设计按《 110kV~ 750kV 架空输电线路设计规范》 (GB 50545-2010)执行; (7)地线按两根普通地线考虑。 (8)10mm及以下冰区直线塔平均呼高及水平档距利用率: 项目 电压 (kV) 地 形 平丘 山地 高山 直线塔平均呼高 500 32 36 36 220 20.5 24 25 110 17.5 21 21.5 水平档距利用率 85% 82% 80% (9)10mm及以下冰区单公里

平面应力状态概述
为了研究受力构件内某一点处的应力状态,可以围绕该点取出一个单元体(形状为立方体,如图空间应力状态时的单元体),单元体各边长均为无穷小量,若单元体有一对平面上的应力为零,即不等于零的应力分量均处于同一坐标平面内(如图 平面应力状态),则称为平面应力状态。
若主应变是沿着一个主轴伸长,而沿另一主轴纯剪(非旋转应变)缩短,但是两者的应变量的绝对值相同,则一个内接的菱形在变形后变成一个钝角和锐角互换位置的菱形。此时,其面积、体积和应变轴的方位都不发生变化,在与主应变轴呈45°的截面上,所以剪切是拉-压二向应力状态。
在材料力学中通常将单元体的四个侧面上只有剪应力而没有正应力作用的情况称为纯剪应力状态(纯剪状态),而更一般的纯剪状态是单元体的六个侧面上仅有剪应力而无正应力作。
在杆件中一点处的应力状态由其横截面上的正应力就可以完全确定,这样的应力状态就是单轴应力状态。单元体在两对相互垂直的平面上只有切应力而没有正应力的状态,是纯剪切应力状态。应力状态(stress state)指的是物体受力作用时,其内部应力的大小和方向不仅随截面的方位而变化,而且在同一截面上的各点处也不一定相同。应变状态理论则研究指定点处的不同方向的应变之间的关系。应力状态理论是强度计算的基础。 2100433B
根据产生预应力的方式,预应力衬砌分为:
①拉筋式衬砌。其预应力状态由拉张钢筋而形成。
②钢箍式衬砌。其预应力状态由分布在衬砌混凝土外面的钢箍的紧束作用而形成。
③锚束式衬砌。其预应力状态由张拉紧穿在衬砌内部的锚束而形成。
④压浆式衬砌。其预应力状态在衬砌背后通过对围岩及其与衬砌间的空隙进行离压灌浆而形成。
- 相关百科
- 相关知识
- 相关专栏
- 应力腐蚀机理的多层次及跨尺度关联研究
- 应力腐蚀的力-电耦合机理研究
- 应力腐蚀破裂断裂韧性
- 应力腐蚀裂纹
- 应力范围
- 应力试验机
- 应力路径非饱和土三轴仪
- 应力集中区
- 应变遥测技术
- 应城个人房屋抵押登记指南
- 应城房屋租赁备案登记指南
- 应对地球危机的设计之道
- 应对随机间歇式扰动的备用调度协调优化研究
- 应急式太阳能Ipad 充电
- 应急管理信息化建设
- 应急管理部上海消防研究所
- 引水隧洞工程中热应力中对围岩表层稳定性的影响分析
- 张峰水库2号倒虹预应力钢筒混凝土管道安装施工工艺
- 中国预应力混凝土管桩的发展状况及同日本管桩的差距
- 在小桥涵软基处理中如何运用预应力混凝土管桩的分析
- 无收缩预应力混凝土高性能灌浆材料与应用
- 岳阳洞庭湖大桥50m跨连续箱形梁桥三向预应力施工
- 有粘结预应力结构施工过程中的应力损失控制技术
- 应力波无损检测技术及其在木结构古建筑保护中的应用
- 中国国际航空公司北京市内货运中心框架梁预应力施工
- 有粘结预应力混凝土空心无梁楼盖结构设计分析与
- 振弦式锚杆应力计在腾龙桥一级水电站左岸边坡的应用
- 宜兴抽水蓄能电站地下厂房预应力锚索施工技术
- 有限元法与材料力学方法在闸墩门槽应力计算中的对比
- 整体式先张法预应力混凝土复合圆管涵洞的结构及安装
- 应力吸收层在水泥混凝土路面白加黑工程中的应用
- 振弦式钢筋计在预应力管桩成桩过程中的安装工艺