斜面分类

从山顶到山脚的倾斜面叫斜面，也叫斜坡或山坡。在地图上明确斜面的具体形状，对定向越野有一定价值。斜面按其形状可分为：实地坡度基本一致的斜面叫等齐斜面，全部斜面均可通视。地图上，从山顶到山脚，间隔基本相等的一组等高线，表示为等齐斜面。

凸形斜面

实地坡度为上缓下陡的斜面叫凸形斜面，部分地段不能通视。地图上，从山顶到山脚，间隔为上面稀、下面密的一组等高线，表示为凸形斜面。

凹形斜面

实地坡度为上陡下缓的斜面叫凹形斜面，全部斜面均可通视。地图上，从山顶到山脚，间隔为上面密、下面稀的一组等高线，表示为凹形斜面。

波状斜面

实地坡度交叉变换、陡缓不一、成波状形的不规则斜面叫波状斜面，若干地段不能通视。地图上，表示该状斜面的等高线间隔稀密不均，没有规律。

物体静止在斜面上受到这些力：物体自身的重力（G），斜面对之的支持力（F_支），对物体的摩擦力（f_静）等。已知斜面的倾角和物体的重力时，我们可以求出另外的两个力：

设斜面倾角为θ，其他和上述一样，则我们把重力分解成沿着斜面的垂线向下的力F₁（F₁=F_支）和平行于斜面向下的力F₂。（当物体静止在斜面上时，F₂=f。注意到这里的施力物体是地球，不是斜面上的物体），建立平行四边形后，我们可以看到重力边和F₂的夹角为90-θ，因此：

因此拉力的值为：

斜面与平面的倾角越大，斜面较短，则省力越小，但省距离。斜面在生活中有广泛的应用，如盘山公路、搬运滚筒、斜面传送带等。在不计算任何阻力时，斜面的机械效率为100%，如果摩擦力很小，则可达到很高的效率。即用F₂表示力，s表示斜面长，h表示斜面高，物重为G。不计无用阻力时，根据功的原理，可得：F₂s=Gh。

斜面（inclined plane）是一种倾斜的平板，能够将物体以相对较小的力从低处提升至高处，但提升这物体的路径长度也会增加。斜面是古代希腊人提出的六种简单机械之中的一种。假若斜面的斜率越小，即斜面与水平面之间的夹角越小，则需施加于物体的作用力会越小，但移动距离也越长；反之亦然。假设移动负载不会造成能量的储存或耗散，则斜面的机械利益是其长度与提升高度的比率。

在日常生活中，时常会使用到斜面。行驶车辆的坡道是一种常见的斜面；卡车装载大型货物时，常会在车尾斜搭一块木板，将货物从木板上往上推，所应用的也是斜面的理论。

在中国的战国时期，墨子所著作的《墨子》一书中，也有叙述斜面与其省力的原理。

斜面是古希腊人提出的六种简单机械之中的一种。亚历山大的帕普斯（290年－350年）在著作《数学汇编》（《Mathematical Collection》），第八卷里尝试解析斜面的重物平衡问题。他似乎是古希腊唯一做这类研究的几何学者。虽然他的方法并不正确，但给予后来的学者极大的启发。欧洲物理学者尼摩的约但努斯传授的一位无名氏学生于十三世纪撰写了著作《约但努斯论述重量理论之书》（《Jordanus's Book on the Theory of Weight》）。这本书后来印版发行于1565年。在这本书里，应用约但努斯原创的“位形重力”（positional gravity,gravitas secundum situm）概念，首先给出了正确解答。1608年，西蒙·斯特芬发表著作《数学纪要》（《Mathematical Collection》），对于这问题给出正确与精彩的解析，稍后会有更详细叙述。伽利略·伽利莱也花了很多时间，找出问题错误所在，并且用不同方法给出正确答案。

日常生活中所用的螺丝钉，就是斜面原理的最好体现。其他的还有金字塔、楼梯、登机桥、电梯、盘山公路等。

对于一般斜面来说，如果不计算任何的阻力，根据功的原理，斜面的机械效率是100%，但是不可避免存在一些阻力，如摩擦力和空气阻力。下面我们就着摩擦力来计算机械效率。我们用θ表示斜面的倾角，G表示物重，F_l表示拉力，f_m表示摩擦力，μ表示斜面摩擦力系数，s表示斜面长，h表示斜面高，W_y表示有用功，W_z表示总功，W_e表示额外功，而F2是顺着斜面向下的分力，这些都在“受力情况”一节有提到。

则它的机械效率为：

因为我们有：

因为我们有：

即为已知斜面倾角和摩擦系数时的机械效率公式。

斜面斜板

使用可移动式斜板，可以轻易地将货物装上或卸下密斗货车。滑梯是儿童游乐场常见的设施。靠着用滑梯坚硬表面的法向力抵抗重力，工业滑梯可以将易损坏物体（包括人体在内）安全快速地从高处滑下至低处。民用飞机的充气逃生滑梯能够允许乘客从飞机出口紧急撤离滑下至地面。

斜面螺旋

螺旋是围绕着圆柱的斜面形成的简单机械。阿基米德螺旋机是古希腊哲学家阿基米德的许多发明与发现之一。从那时起，人们时常会使用阿基米德螺旋机来搬动很多不同种类的物质，像水、矿物、谷物等等。

斜面楔子

楔子是两个背靠背的斜面组成的简单机械。楔子可以用来将物件分开，其操作原理主要是将作用于楔子向下的力转变为对物件水平的力，而这两个力几乎垂直。常见应用楔子原理的工具包括斧头。

斜面单摆

单摆是由一条绳子与一个摆锤组成的实验仪器，其摆锤的运动轨迹是一个对称朝上的圆弧。这圆弧可以分割为很多小圆弧，每两个相邻的小圆弧最多只相交于一个端点。连接每个小圆弧的两个端点之间的线段称为弦。每个弦都可以视为斜面。令增加分割的数量至无限多，每一个小圆弧的弧长趋向为无穷小的极限，所得到无限多小圆弧的对应斜面会组成原本的圆弧。所以，在任意时间，单摆的摆锤可以想像为移动于某特定斜率的斜面。

配制方法

一般试管斜面的配制方法：将琼脂粉加入培养基后煮沸，使其全部溶解，再分装至试管中，再灭菌。问题是：你大概没有待琼脂完全溶解，就将其分装至试管，因此试管中的琼脂浓度低于你加入的百分比，而烧杯中残留的琼脂浓度高；也就造成了试管斜面以划破，而烧杯凝固很好。2100433B

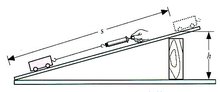
斜面机械效率公式为：η=W_有/W_总=Gh/Fs。（G为物体重量，h为斜面竖直高度，F为拉力大小，s为斜面长度。）

推导公式：η=

（θ为斜面倾角，μ为滑动摩擦系数）

推导过程：如图1，将物体重力垂直分解为垂直于斜面的力F⊥和平行于斜面的力F∥，则：

η=W_有/W_总=Gh/Fs=Gh/(f F')s=Gh/(μF⊥ F∥)s=Gsinθ*s/(μGcosθ Gsinθ)*s=sinθ/μcosθ sinθ=1/(μcotθ 1)(适用于匀速拉动）