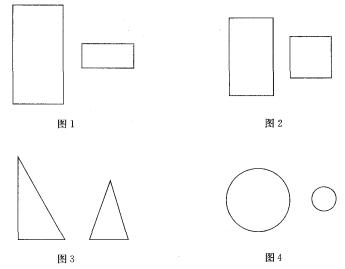
相似图形基本信息
| 中文名称 | 相似图形 | 外文名称 | Similar figures |
|---|
相似图形造价信息
相似图形常见问题
相似图形文献

 2013,6,13相似图形综合测试题讲义1
2013,6,13相似图形综合测试题讲义1
《相似图形》综合测试题 一、精心选一选(每小题 3 分,共 30分) 1.小明同学在复习相似形后, 总结了能够形似的图形, 下面是他给出的几个图形中一定能相似的是 ( ) (A)两个矩形( B)两个平行四边形 (C)两个正方形 (D)两个菱形 2.小丽用纸板做了一个△ ABC准备制作卡片,卡片的三边的长分别是 AC=10cm,BC=15cm,AB=20cm,素 娟看到了也学着制作一个和小丽的形状相同的卡片,她的三角形的最短边为 30cm,则素娟制作的三角形 卡片的周长是( ) (A)120cm (B) 125cm (C) 130cm (D)135cm 3.小亮是一位飞镖爱好着,一次他画了一个△ ACB,其中 AC=21cm,BC=24cm,AB=39cm,又在内部画了△ A′B′C′,其中 A′C′ =7cm,B′C′ =8cm,A′B′=13cm,他能做大每有一镖都能打中△ A
定理1 位似图形必彼此真正相似 。
定理2 若两非合同的真正相似图形有一双对应直线互相平行或重合,则它们必是位似图形。
注 必须注意,即使两真正相似图形的每双对应顶点连线共点,但这两图形未必是位似的,例如在下图中所绘的△ABC与△A'B'C',它们不但真正相似,且有透视中心O,然而它们明明就不是位似图形。
定理3 既不合同也不位似的两个真正相似图形,可以接连行一次位似变换和一次旋转将其一形变为他形, 其中相似中心和旋转中心是同一点。
定理4设图形F与F'真正相似但不合同,A与A'是任一双对应点,k是相似比。若内外分钱段AA'于M、N,使
定理5 非合同的两个镜象相似图形,可以接连行一 次反射和一次位似变换将其一形变为另一形,其中反射轴通过相似中心。
定理6 非合同的两个镜象相似图形的两条二重线,内外分每双对应点的连接线所得的分比,都等于两形的相似比 。
真正相似是一种特殊相似形,设图形F与F′是相似形,在图形F上任取不共线 三点A,B,C,它们在图形F′上的对应点分别是A′,B′,C′(如图1),若△ABC和△A′B′C′的方向相同,即三对对应点的排列(沿周界ABCA与A′B′C′A′的环绕方向)或同为顺时针方向或同为逆时针方向,则称图形F与图形F′真正相似。真正相似图形的重要特例是真正相似三角形。当△ABC与△A′B′C′相似,且沿周界ABCA与沿周界A′B′C′A′的环绕方向相同,即同为逆时针方向或同为顺时针方向,则这两个三角形是真正相似三角形 。
杠杆缩放仪(leer pantograph)是指由四根等长金属杆构成平行四边形的缩小或放大绘图仪器。图1中A为固定不动的极点,B和C分别为描针和铅笔的位置。使用时按照缩放比例调整三点在一直线上,将描针沿图形线位描画移动,即绘出相似图形。按放大或缩小目的不同,B、C可互换位置。常与多倍仪联用 。
- 相关百科
- 相关知识
- 相关专栏
- 平面设计图形联想创意
- 区间值直觉模糊集相似性的信息安全风险评估方法研究
- 测量实践中城市地籍图形管理信息系统架构设计
- 改进相似权可拓理论的大跨径公路桥梁抗风稳定性评价
- 广联达造价软件图形算量指导资料
- RT消防控制室图形显示装置图形显示装置使用说明书V
- CAD图形插入及其他OFFICE文档方法
- AutoCAD图形参数化设计在快速绘图过程中应用
- 图形自动生成工程量预算软件在实际应用中的几点体会
- 图形设计技术及其在组合式空调CAD中的应用
- cad图形快速导入ansys建模方法
- 地基与均匀地基承载力之间的相似关系
- DX001建筑电气工程设计常用图形和文字符号
- FMS8000型消防控制室图形显示装置操作说明书
- 广联达图形算量图文教程
- 测绘工程CAD5精确绘制图形与控制图形显示