香农定理
香农定理给出了信道信息传送速率的上限(比特每秒)和信道信噪比及带宽的关系。香农定理可以解释现代各种无线制式由于带宽不同,所支持的单载波最大吞吐量的不同。
在有随机热噪声的信道上传输数据信号时,信道容量Rmax与信道带宽W,信噪比S/N关系为: Rmax=W*log2(1+S/N)。注意这里的log2是以2为底的对数。
香农定理基本信息
| 中文名称 | 香农定理 | 外文名称 | Shannon Theory |
|---|---|---|---|
| 信道容量 | Rmax与信道带宽W | 描述了 | 有限带宽 |
| Rmax | =W*log2(1+S/N) | ||
香农定理用来求信道的最大传输速率,即信道容量,当通过信道的信号速率超过香农定理的信道容量时,误码率显著提高,信息质量严重下降。需要指出的是这里的信道容量只是理论上可以达到的极限,实际如何达到,该定理不能说明。
香农定理造价信息
香农定理常见问题
-
80*80+50*50后开方。
-
没有圆切角定理,只有弦切角定理:弦切角等于它所夹的弧对的圆周角
-
首先更正一下,是弦切角,老沈瞎说呢。你把图画出来,AB是圆O切线,AC是弦。做过切点A的直径,交圆O于A、D。连接B、D。证明:因为AD是圆O直径,AB是圆O切线所以∠C=90°=∠BAD所以∠BAC...
香农定理文献
割线定理
定义
从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。
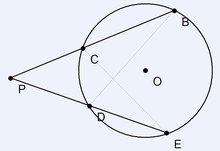
从圆外一点P引两条割线与圆分别交于C,B,D,E,则有 PC·PB=PD·PE。如下图所示。 (PA是切线)
英文名称
Secant Theorem
概述
割线定理为圆幂定理之一(切割线定理推论),其他二为:
切割线定理
相交弦定理
证明
如图直线PB和PE是自点P引的⊙O的两条割线,则PC·PB=PD·PE.
证明:连接CE、DB
∵∠E和∠B都对弧CD
∴由圆周角定理,得 ∠E=∠B
又∵∠EPC=∠BPD
∴△PCE∽△PDB
∴PC:PD=PE:PB, 也就是PC·PB=PD·PE.
比较
割线定理与相交弦定理,切割线定理通称为圆幂定理。
相交弦定理、切割线定理以及它们的推论统称为圆幂定理。一般用于求线段长度。
切割线定理定理
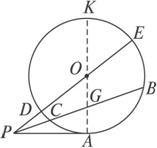
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。是圆幂定理的之一。
几何语言:∵PT切⊙O于点T,PDC是⊙O的割线
∴PT²=PD·PC(切割线定理)
推论:
从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等
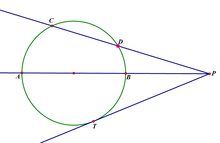
几何语言:∵PT是⊙O切线,PBA、PDC是⊙O的割线
∴PD·PC=PA·PB(切割线定理推论)(割线定理)
由上可知:PT²=PA·PB=PC·PD
- 相关百科
- 相关知识
- 相关专栏
- FX1N
- mega2560
- STM32F4Discovery
- FX2N系列
- UF6
- FX1N-60MT-D
- FX3U-4AD-ADP
- 暖通空调设计300问
- 吉时利2700数据采集器
- STK500
- FX3U-4DA-ADP
- FX3U-4AD-PT-ADP
- Labjack U12
- 串口控制器
- 中国机电产品目录,第5册
- FX1S系列
- 信贷扩张、房地产价格波动与银行稳定理论及其经验分析
- 合力矩定理在土建工程中的应用
- 实验三戴维南定理验证及有源单口网络等效参数的测量
- 对新火电厂大气污染物排放标准脱硫规定理解
- Hermite插值神经网络权值和结构确定理论
- 施工企业共产党员坚定理想信念措施
- 工业建筑可靠性鉴定理论与应用
- 受施工扰动影响土体环境稳定理论与变形控制
- 稳定理论的低碳钢托架结构参数的优化设计
- 可变模糊集对立统一定理的水安全评价
- 数值分析课程中定理反讲教学方式
- 压力容器金属材料进厂验收最新规定理解
- 安全阀阀芯传感器标定理论与验证技术
- 不确定理论的电力系统脆弱性评估
- 压差旁通阀压差值再设定理论计算
- 岩体等效强度参数确定理论和方法