椭圆曲线和模型式引论
椭圆曲线和模型式引论基本信息
| 中文名 | 椭圆曲线和模型式引论 | 出版社 | 世界图书出版公司 |
|---|---|---|---|
| 页 数 | 248 页 | ISBN | 750626014X |
| 品 牌 | 世界图书出版公司北京公司 | 作 者 | N.Koblitz |
| 出版日期 | 2003年6月1日 | 开 本 | 24 开 |
| 定 价 | 27.00 | ||
Preface to the First Edition
Preface to the Second Edition
CHAPTER I From Congruent Numbers to Elliptic Curves
1. Congruent numbers
2. A certain cubic equation
3. Elliptic curves
4. Doubly periodic functions
5. The field of elliptic functions
6. Elliptic curves in Weierstrass form
7. The additionclaw
8. Points of finite order
9. Points over finite fields, and the congruent number problem
CHAPTER II The Hasse-Weil L-Function of an Elliptic Curve
I. The congruence zeta-function
2. The zeta-function of E
3. Varying the primep
4. The prototype: the Riemann zeta-function
5. The Hasse-Weil L-function and its functional equation
6. The critical value
CHAPTER III Modular forms
1. SL2(Z) and its congruence subgroups
2. Modular forms for SL2(Z)
3. Modular forms for congruence subgroups
4. Transformation formula for the theta-function
5. The modular interpretation, and Hecke operators
CHAPTER IV Modular Forms of Half Integer Weight
1. Definitio ns and examples
2. Eisenstein series of half integer weight for (4)
3. Hecke operators on forms of half integer weight
4. The theorems of Shimura, Waldspurger, Tunnell, and the congruent number problem
Answers, Hints, and Referen es for Selected Exercises
Bibliography
Index2100433B
椭圆曲线和模型式引论造价信息
My purpose is to make the subject accessible to those who find it hard to read more advanced or more algebraically oriented treatments. At the same time I want to introduce topics which are at the forefront of current research. Down-to-earth examples are given in the text and exercises, with the aim of making the material readable and interesting to mathematicians in fields far removed from the subject of the book.
椭圆曲线和模型式引论常见问题
-
具体怎么样的呢,你用CAD随便画一下给我们看看
-
不是有个专门画圆弧的吗,点击那个按钮后选择相应项目就可以了
-
用凸曲线,貌似如此,同求大神解答
椭圆曲线和模型式引论文献

 一类超奇异超椭圆曲线的Tate对实现
一类超奇异超椭圆曲线的Tate对实现
针对奇特征域F pn上的超奇异超椭圆曲线y2=xp-ax-b,其中p≡1,3(mod4),a,b∈F p且a是p的一个本原根,该文研究了曲线关于双线性对的相关性质,并进一步提出了基于Tate对的快速算法。该算法改进了传统的Miller算法,并将Tate对的运算量减少了至少56%。

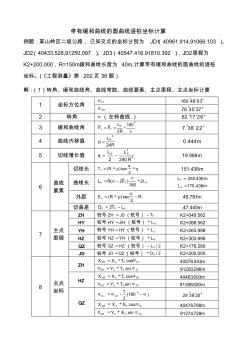 带有缓和曲线的圆曲线逐桩坐标计算例题
带有缓和曲线的圆曲线逐桩坐标计算例题
带有缓和曲线的圆曲线逐桩坐标计算 例题:某山岭区二级公路,已知交点的坐标分别为 JD1(40961.914,91066.103 )、 JD2(40433.528,91250.097 )、JD3(40547.416,91810.392 ),JD2里程为 K2+200.000,R=150m,缓和曲线长度为 40m,计算带有缓和曲线的圆曲线的逐桩 坐标。(《工程测量》第 202页 36题) 解:(1)转角、缓和曲线角、曲线常数、曲线要素、主点里程、主点坐标计算 1 坐标方位角 12 3084160 23 730378 2 转角 (左转曲线 ) 627182 3 缓和曲线角 180 2R LS ho 22837 4 曲线内移值 R L p S 24 2 m444.0 5 切线增长值 2 3 2402 R LLq SS m988.19 6 曲线 要素 切线长 qpRTh 2 tan)( m438.
概念:具有某种共同属性的椭圆或双曲线的集合,称为椭圆系或双曲线系。
几种常见的椭圆系或双曲线系方程:
(1)x^2/(c^2 t) y^2/t=1(半焦距为c且c≠0),当t>0时,表示共焦点(±c,0)的椭圆系;当-c^2 (3)与椭圆x^2/a^2 y^2/b^2=1(a^2>b^2)共焦点的曲线系方程可设为x^2/(a^2-λ) y^2/(b^2-λ),当λ(4)渐近线方程为x/a±y/b=1或y=±(b/a)x的双曲线系可设为x^2/a^2-y^2/b^2=λ(λ≠0)。2100433B
椭圆模板是指一种呈椭圆形的模板(TEMPLATE),在制图和广告设计时用来绘制椭圆形和曲线。椭圆模板可分为两类。有一类模板上所有的椭圆形都具有相同的投影角度(例如45度),只是主轴的长度不同。另一类模板则包含几个呈现不同角度的椭圆形,通常从15度到60度,每五度一增,共有十种不同的角度。亦见FRENCH CURVE。
浮雕细工在浮雕(RELIEF)表层上制造凸起的人物或图案的一种工法。有在皮革、纸张、金属或布上的轧纹,以及书籍封面、各种类型的装饰艺术等,制作时通常会使用一对相称的模具在正反两面加压,把凸印模具放在反面而凹印模在正面。至于铜板的浮雕制作则更接近于铸造(striking)而不是浮雕细工。用于木头上的古老浮雕细工是使用像凿子这样钝器,沿着事先画好的图案边线,把表层刨平到与凹陷图案等高,然后浸湿整个表面。湿气会使得压缩过的区域升高到原来的高度,并且突出于刨过的表面。至于以手工而不是用机械打造的金属薄片浮雕则称为锤揲法(REPOUSS )。2100433B
Mamdani教授最初所用的模糊变量分为连续型和离散型两种型式,因此隶属度函数的型式也可以分为连续型与离散型两种。由于语言变量及相对应隶属度函数选择的不同,将形成许多不同的模糊控制器架构;下面将对各隶属度函数的型式加以介绍:
1. 连续型隶属度函数
模糊控制器中常见的连续型隶属度函数有下列三种:
(1)吊钟形(2)三角形(3)梯形
2. 离散型隶属度函数
Mamdani教授除了使用连续型全集合之外,也使用了由13个元素所构成的离散合。由于用微处理机计算时使用整数比用〔0,1〕之间的小数更方便,模糊集合的隶属度均以整数表示。
模糊控制理论发展之初,大都采用吊钟形的隶属度函数,而近几年几乎都已改用三角形的隶属度函数,这是由于三角形隶属度函数计算比较简单,性能与吊钟形几乎没有差别。
- 相关百科
- 相关知识
- 相关专栏
- 椭圆曲线密码系统的算法结构与VLSI实现
- 椭圆曲面
- 椿萱茂
- 楔体型滑坡
- 楔形体
- 楔横轧
- 楔缝式锚杆
- 楔轧
- 楚北水利堤防纪要
- 楚国城旅游开发有限公司
- 楚天时代(湖北)文旅策划有限公司
- 楚岳(惠州)热传科技有限公司
- 楚攀天然气管道
- 楚雄大永高速公路投资建设开发有限公司
- 楚雄州道路交通管理志
- 楚雄州青山嘴水库工程建设管理局
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 在全县非煤矿山和危化企业安全生产工作会议上的讲话
- 支持并行工程和智能CAPP的制造资源建模技术
- 有限元法在软土浅埋隧道施工过程的动态模拟中的应用
- 新型基于热力学法的水泵效率数学模型及应用
- 影响铁路电力迁改总承包工程因素的模糊综合评价
- 引入PPP模式的高标准农田建设及财政支持体系创新
- 云计算对企业信息化系统建设和运营的影响分析和改进
- 政府和社会资本合作(PPP)项目物有所值评价
- 新的基于NGA/PCA和SVM的特征提取方法
- 中华人民共和国国家标准建设工程工程量清单计价规范
- 应用型人才培养模式下高校机电工程综合实践改革探索
- 永春县农田水利设施产权制度改革和运行管护机制试点
- 异形人工挖孔桩和预应力土层锚杆组合在基坑中的应用
- 政府投资建设项目在财务管理上面临的风险和应对措施
- 指路标志(里程碑和百米碑)施工记录表