凸透镜的成像规律与凹透镜区别
结构不同
凸透镜是由两面磨成球面的透明镜体组成,凸透镜两边薄中间厚。
凹透镜是由两面都是磨成凹球面透明镜体组成,凹透镜两边厚中间薄。
.
对光线的作用不同
凸透镜主要对光线起会聚作用
凹透镜主要对光线起发散作用
成像性质不同
凸透镜是折射成像,成的像可以是 正立、倒立;虚像、实像;放大、缩小。起聚光作用。
凹透镜是折射成像,只能成缩小的正立虚像。起散光作用。
透镜与面镜
透镜(包括凸透镜)是使光线透过,使用光线折后成像的仪器,光线遵守折射定律。
面镜(包括凸面镜)不是使光线透过,而是反射回去成像的仪器,光线遵守反射定律。
凸透镜的成像规律造价信息
凸透镜可以成倒立放大、等大、缩小的实像或正立放大的虚像。可把平行光会聚于焦点,也可把焦点发出的光线折射成平行光。凸面镜主要用扩大视野。凸透镜的成像规律 物距(u)像距(v)倒立、正立放大、缩小虚像、实像 应用特点:
1.u>2f f<v<2f 倒立、缩小、实像 照相机
2.u=2v=2f倒立、等大、实像 测焦距大小分界点f<u<2 fv>2 f倒立、放大、实像 投影仪 幻灯机 u=f//// 探照灯获得平行光源虚实分界点 倒、正分界点
3.u<fv>u与物同侧 正立、放大、虚像 放大镜虚像在物体同侧 物像同侧 (1)二倍焦距以外,倒立缩小实像;〈这里所指的一倍焦距是说平行光源通过透镜汇聚的那一点到透镜光心的距离,那么两倍焦距就是指2倍远的地方〉
二倍焦距,倒立等大实像;
一倍焦距到二倍焦距,倒立放大实像;
一倍焦距不成像;一倍焦距以内,正立放大虚像;
成实像物和像在凸透镜异侧,成虚像在凸透镜同侧。
(2)
一倍焦距分虚实
两倍焦距分大小
物近像远像变大
物远像近像变小
凸透镜成像规律表格
物体到透镜中心的距离u 像的正倒像的大小像的虚实 像到透镜中心的距离v 应用实例物距和像距的关系
(u是物距 v是像距 f是焦距)
u>2f 倒立 缩小的 实像 2f>v>f 照相机 u>v
u=2f 倒立 等大的 实像 v=2f可用来测量凸透镜焦距 u=v
2f>u>f 倒立 放大的 实像 v>2f 放映机,幻灯机,投影机u<v
u=f 不成像 平行光源: 探照灯 \
u<f 正立 放大的 虚像 v>u 虚像在物体同侧 放大镜\
为了研究各种猜想,人们经常用光具座进行试验。
蜡烛的焰心,凸透镜中心,光屏中心应尽量保持在同一水平高度上。
(3)凸透镜成像还满足1/v+1/u=1/f
利用透镜的特殊光线作透镜成像光路:
(1)物体处于2倍焦距以外
(2)物体处于2倍焦距和1倍焦距之间
(3)物体处于焦点以内
(4)凸透镜成像光路 实验研究凸透镜的成像规律是:当物距在一倍焦距以内时,得到正立、放大的虚像;在一倍焦距到二倍焦距之间时得到倒立、放大的实像;在二倍焦距以外时,得到倒立、缩小的实像。
该实验就是为了研究证实这个规律。实验中,有下面这个表:
物 距 u 像的性质 像的位置
正立或倒立 放大或缩小虚像或实像 与物同侧与异侧像距v
u>2f 倒立缩小 实像异侧 f<v<2f
u=2f 倒立等大 实像异侧 v=2f 此时物体与像的距离是最小的,即4倍焦距。
f<u<2f 倒立放大 实像异侧v>2f
u=f 不成像 v无限大(平行光源,如:探照灯)
u<f 正立 放大 虚像 同侧 u,v同侧
这就是为了证实那个规律而设计的表格。其实,透镜成像满足透镜成像公式:
1/u(物距)+1/v(像距)=1/f(透镜焦距)
照相机运用的就是凸透镜的成像规律
镜头就是一个凸透镜,要照的景物就是物体,胶片就是屏幕
照射在物体上的光经过漫反射通过凸透镜将物体的像成在最后的胶片上
胶片上涂有一层对光敏感的物质,它在曝光后发生化学变化,物体的像就被记录在胶卷上
至于物距、像距的关系与凸透镜的成像规律完全一样
物体靠近时,像越来越远,越来越大,最后再同侧成虚像。
物距增大,像距减小,像变小;物距减小,像距增大,像变大。
一倍焦距分虚实,二倍焦距分大小。
凸透镜成像规律表:实像,物近像远像变大;虚像,物远像远像变大
(4)当成虚像时,物、像的左右一致,上下一致;当成实像时,物、像的左右相反,上下相反.。
(5)凸透镜成像的两个分界点:2f点是成效放大缩小实像的分界点;f点是成实像虚像的分界点。
凸透镜的成像规律与凹透镜区别常见问题
-
凹面镜和凸面镜都是反射镜,区别是前者用球的内表面做反射面,后者是用球的外表面做反射面;前者对平行入射光的作用是会聚的,后者是发散的;前者成倒立缩小的实象,后者成缩小正立的虚象。凹透镜与凸透镜都是利用光...
-
1、凹透镜也称为——发散透镜 2、凸透镜也称为——会聚透镜 凸透镜拥有放大作用。凸透镜二倍焦距分大小,一倍焦距分实虚正倒。 将平行光线(如阳光)平行于主光轴(凸透镜两个球面的球心的连线称为此透镜的主光...
-
凸透镜是根据光的折射原理制成的。凸透镜是中央较厚,边缘较薄的透镜。凸透镜分为双凸、平凸和凹凸(或正弯月形)等形式,凸透镜有会聚作用故又称聚光透镜,较厚的凸透镜则有望远、会聚等作用,这与透镜的厚度有关。
凸透镜的成像规律与凹透镜区别文献

 凸透镜教学设计
凸透镜教学设计
今泰学院推荐文档 第 1 页 共 5 页 凸 透 镜教学设计 Teaching design of convex lens 今泰学院推荐文档 第 2 页 共 5 页 凸 透 镜教学设计 前言:小泰温馨提醒,自然指的是自然界的现象,以及普遍意义上的生命。人造物体及人 类间的相互作用并不视为自然的一部分,除非被界定的是人性或“大自然全体”。本教案 根据自然课程标准的要求和针对教学对象是小学生群体的特点,将教学诸要素有序安排, 确定合适的教学方案的设想和计划、并以启迪发展学生智力为根本目的。便于学习和使用, 本文下载后内容可随意修改调整及打印。 1、通过本课教学,使学生知道凸透镜有成像作用和成像大小的规 律,了解凸透镜的应用。 2、培养学生的实验能力(初步学会做凸透镜成像的实验)、 归纳概括能力(通过反复实验,归纳凸透镜成像大小的规律)和 制作能力(制作土照相机) 3、通过实验和制作,培养

 大直径平凸透镜面形的阴影检验法
大直径平凸透镜面形的阴影检验法
本文分析了使用样板检测大口径平凸透镜的弊端,细述了用刀口仪检测大直径凸面透镜的相关计算方法和操作过程,并用实例加以证明。
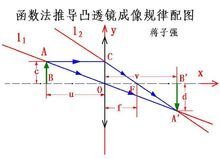
凸透镜成像规律推导方法
凸透镜的成像规律是1/u+1/v=1/f(即:物距的倒数与像距的倒数之和等于焦距的倒数。一共有两种推导方法 。分别为"几何法"与"函数法"
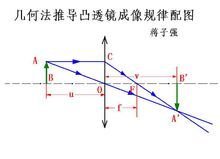
几何法
【题】如右图 ,用几何法证明1/u+1/v=1/f。 【解】∵△ABO∽△A'B'O
∴AB:A'B'=u:v
∵△COF∽△A'B'F
∴CO:A'B'=f:(v-f)
∵四边形ABOC为矩形
∴AB=CO
∴AB:A'B'=f:(v-f)
∴u:v=f:(v-f)
∴u(v-f)=vf
∴uv-uf=vf
∵uvf≠0
∴(uv/uvf)-(uf/uvf)=vf/uvf
∴1/f-1/v=1/u
即:1/u+1/v=1/f
答
函数法
【题】 如右图 ,用函数法证明1/u+1/v=1/f。 【解】一基础
右图为凸透镜成像示意图。
其中c为成像的物体长度,d为物体成的像的长度。u为物距,v为像距,f为焦距。
步骤
(一)为便于用函数法解决此问题,将凸透镜的主光轴与平面直角坐标系的横坐标轴(x轴)关联(即重合),将凸透镜的理想折射面与纵坐标轴(y轴)关联,将凸透镜的光心与坐标原点关联。则:点A的坐标为(-u,c),点F的坐标为(f,0),点A'的坐标为(v,-d),点C的坐标为(0,c)。
(二)将AA',A'C双向延长为直线l1,l2,视作两条函数图象。由图象可知:直线l1为正比例函数图象,直线l2为一次函数图象。
(三)设直线l1的解析式为y=k1x,直线l2的解析式为y=k2x+b
依题意,将A(-u,c),C(0,c),F(f,0)代入相应解析式得方程组:
c=-u·k1
c=b
0=k2f+b
把k1,k2当成未知数解之得:
k1=-(c/u), k2=-(c/f)
∴两函数解析式为:
y=-(c/u)x, y=-(c/f)x+c
∴两函数交点A'的坐标(x,y)符合方程组
y=-(c/u)x
y=-(c/f)x+c
∵A'(v,-d)
∴代入得:
-d=-(c/u)v
-d=-(c/f)v+c
∴-(c/u)v=-(c/f)v+c=-d
∴(c/u)v=(c/f)v-c=d
cv/u=(cv/f)-c
fcv=ucv-ucf
fv=uv-uf
∵uvf≠0
∴fv/uvf=(uv/uvf)-(uf/uvf)
∴1/u=1/f-1/v
即:1/u+1/v=1/f

成像公式推导方法
凸透镜的成像规律是1/u+1/v=1/f(即:物距的倒数与像距的倒数之和等于焦距的倒数。)一共有两种推导方法 。分别为"几何法"与"函数法"
几何法
【题】如右图 ,用几何法证明1/u+1/v=1/f。
【解】∵△ABO∽△A'B'O
∴AB:A'B'=u:v
∵△COF∽△A'B'F
∴CO:A'B'=f:(v-f)
∵四边形ABOC为矩形
∴AB=CO
∴AB:A'B'=f:(v-f)
∴u:v=f:(v-f)
∴u(v-f)=vf
∴uv-uf=vf
∵uvf≠0
∴(uv/uvf)-(uf/uvf)=vf/uvf
∴1/f-1/v=1/u
即:1/u+1/v=1/f
函数法
【题】 如右图 ,用函数法证明1/u+1/v=1/f。
【解】一基础
右图为凸透镜成像示意图。
其中c为成像的物体长度,d为物体成的像的长度。u为物距,v为像距,f为焦距。
步骤
(一)为便于用函数法解决此问题,将凸透镜的主光轴与平面直角坐标系的横坐标轴(x轴)关联(即重合),将凸透镜的理想折射面与纵坐标轴(y轴)关联,将凸透镜的光心与坐标原点关联。则:点A的坐标为(-u,c),点F的坐标为(f,0),点A'的坐标为(v,-d),点C的坐标为(0,c)。
(二)将AA',A'C双向延长为直线l1、l2,视作两条函数图象。由图象可知:直线l1为正比例函数图象,直线l2为一次函数图象。
(三)设直线l1的解析式为y=k1x,直线l2的解析式为y=k2x+b
依题意,将A(-u,c),C(0,c),F(f,0)代入相应解析式得方程组:
c=-u·k1
c=b
k2f+b=0
把k1,k2当成未知数解之得:
k1=-(c/u)
k2=-(c/f)
∴两函数解析式为:
y=-(c/u)x
y=-(c/f)x+c
∴两函数交点A'的坐标(x,y)符合方程组
y=-(c/u)x
y=-(c/f)x+c
∵A'(v,-d)
∴代入得:
-d=-(c/u)v
-d=-(c/f)v+c
∴-(c/u)v=-(c/f)v+c
(c/u)v=(c/f)v-c
cv/u=(cv/f)-c
fcv=ucv-ucf
fv=uv-uf
∵uvf≠0
∴fv/uvf=(uv/uvf)-(uf/uvf)
∴1/u=1/f-1/v
即:1/u+1/v=1/f
- 相关百科
- 相关知识
- 相关专栏
- Maya 2010技法精粹
- Maya2008中英文命令速查手册
- Maya必备手册基础篇
- Maya2008从入门到精通
- Maya 2008标准教程
- Zbrush高精模型与静帧艺术渲染精粹
- 移动式工具柜
- 风干机
- 风干胶片
- 熟食展示柜
- 熟食柜
- 强流风干机
- 熟食保鲜柜
- 风干土
- 风干浆
- 激光灯
- 引嫩工程扩建区土壤水盐动态与防治土壤盐碱措施
- 中国工程图学学会成立工程与制造系统集成化分会
- 影响萘高效减水剂与普通硅酸盐水泥适应性的关键因素
- 智能建筑工程报警与电视监控系统前端设备的安装施工
- 应对水源突发污染的城市供水应急处理技术与应用
- 宜兴沈北路二号桥大直径钻孔灌注桩的施工与质量控制
- 招远电视台制作播出系统数字化改造工程的设计与实践
- 正压送风对降低污水厂设备腐蚀的作用与实践(论文)
- 云南郝家河砂岩型铜矿床地质特征与接替资源勘查成果
- 政府与社会资本合作(PPP)项目审计监督理论
- 应用清单招标与经评审的最低投标价法评标的几点思考
- 智能化技术在电气工程自动化控制中的应用与实践研讨
- 中国电动汽车充电站市场现状与投资分析报告
- 智能小区以太接入交换机SNMP代理设计与实现
- 智能建筑虚拟仪器监控系统与控制网络的接口技术
- 有色金属技术经济院与广亚铝业签署战略合作协议