统计设计种类
通常,统计研究对象内容的设计可称为横向设计。统计工作过程的设计则可称为纵向设计。
(1)整体设计和专项设计:按研究对象范围划分。
整体设计是将统计研究内容作为一个整体,对其进行全面的设计。
专项设计是从研究对象的某一部分出发,对该方面的具体内容进行设计。
一个企业统计工作的设计、全国工业统计工作的设计是整体设计。
专项设计是对认识对象的某个方面、某个部分进行的设计。例:人口普查的设计、工业企业经济效益统计的设计。
(2)全过程设计和单阶段设计:按工作阶段划分。
全过程设计是对统计工作中经历的各个阶段所进行的全面设计,从确定统计内容、统计指标体系开始到分析硬件 全过程的通盘安排,其中包括统计工作阶段所有的设计方案,及工作阶段间的协调统一。
单阶段设计则是对统计工作过程中某一具体阶段所进行的设计,一般体现某一阶段具体的统计设计方案。
(3)长期设计和短期设计:按时期不同划分。
长期设计是指较长时期的统计设计,如五年以上的统计设计。
短期设计一般是指一年或年度内的统计设计。两年或三年的统计工作设计,一般称为中期统计设计。2100433B
统计设计造价信息
(1)统计是需要高度集中统一的工作。这就要求必须事先制定出经过通盘考虑过的设计方案才能实现。
(2)统计工作不再是仅仅以单项的统计活动为主体,而是要把认识对象作为一个整体来进行全面的、综合的反映和研究。
(3)从认识顺序来讲,统计工作是从对客观对象的定性认识开始的。没有这种定性认识,就不知道去调查什么和怎么调查,也不知道去研究什么和怎么研究。
(4)从统计实践来看,加强和重视统计设计工作对完成整个统计工作,保证统计工作的质量是必需的。
统计设计的内容是对统计研究对象的内容和统计工作过程通盘规划和统筹规划的综合,各项统计工作由于研究目的不同,以统计设计的内容上会存在具体差异,但它们在主要内容上是具有共性的,一般包括以下几个方面:
①统计指标和指标体系;
②与统计指标体系相联系的统计分类和分组;
③搜集统计资料的方法;
④统计工作各个部门和各个阶段的协调与关联;
⑤统计力量的组织和安排。
统计全阶段设计的内容主要有:
①明确规定统计工作的目的;
②确定统计对象的范围;
③规定统计的空间标准和时间标准;
④根据统计研究的目的,制订出调查登记的项目,分类和分组的方法以及统计指标的计算方法;
⑤制定保证统计资料准确性的方法;
⑥规定各个阶段的工作进度,时间安排,各个工作阶段的联系和各阶段的基本方法;
⑦安排好统计工作全过程的组织工作。
统计设计种类常见问题
-
统计墙体砌块,除了要把不同种类砖分开统计,墙厚不同的需不需要分开统计呢?
要区分开的
-
没有快捷方法,只能踏踏实实的按图计算。
-
统计砌块工程量时,要把内外墙分开来统计不、还有不同种类的砖也要分开来统计吗?
统计砌块工程量时,要把内外墙分开来统计 、还有不同种类的砖也要分开来统计,因为他们适用的定额子目 都是不同的 。
统计设计是统计工作实施的基本依据,是使统计工作协调地、有秩序地、顺利地进行的必要条件,是保证以后统计调查、统计整理和统计分析诸阶段工作质量的重要前提。统计设计对整个统计工作起两方面的作用:
①从认识上讲,是对统计总体的定性认识和定量认识的连接点。它将研究对象作为一个整体进行全面的反映和研究,避免统计标准的不统一。
②从工作上讲,它起通盘安排的作用,分清主次先后,按需要和可能采用不同的统计方法,避免重复和遗漏,使统计工作有秩序地顺利地进行。
统计设计是统计工作的首要阶段,是根据统计研究的目的和研究对象的特点,明确统计指标和指标体系,以及对应的分组方法,并以分析方法指导实际的统计活动。其基本任务是制定出各种统计工作方案,是统计工作过程不可缺少的重要环节之一,是统计工作的指导依据。统计设计所制定的方案包括:统计指标体系、统计分类目录、统计报表制度、统计调查方案、统计汇总或整理方案以及统计分析方案等诸多方面的内容。
统计设计种类文献

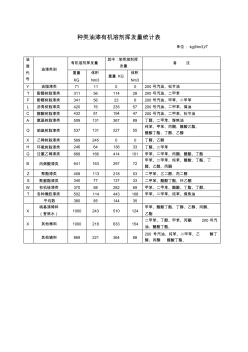 种类油漆有机溶剂挥发量统计表
种类油漆有机溶剂挥发量统计表
种类油漆有机溶剂挥发量统计表 单位: kg(Nm3)/T 油 漆 代 号 油漆类别 有机溶剂挥发量 其中:苯类溶剂挥 发量 备 注 重量 KG 体积 Nm3 重量 KG 体积 Nm3 Y 油脂漆类 71 11 0 0 200 号汽油、松节油 T 酚醛树脂漆类 311 56 114 28 200 号汽油、二甲苯 F 酚醛树脂漆类 341 56 23 6 200 号汽油、甲苯、二甲苯 L 沥青树脂漆类 420 76 235 57 200 号汽油、二甲苯、煤油 C 醇酸树脂漆类 432 81 194 47 200 号汽油、二甲苯、松节油 A 氨基树脂漆类 509 131 367 89 丁醇、二甲苯、煤焦油 Q 硝基树脂漆类 537 131 227 55 纯苯、甲苯、丙酮、醋酸乙酯、 醋酸丁酯、丁醇、乙醇 X 乙稀树脂漆类 569 245 0 0 丁醇、乙醇 H 环氧树脂漆类 246

 纸箱、纸盒的种类和设计
纸箱、纸盒的种类和设计
书山有路勤为径;学海无涯苦作舟 纸箱、纸盒的种类和设计 纸制品包装,是包装工业品中用量最大的种类。纸箱是最主要的 运输包装形式,而纸盒广泛用做食品、医药、电子等各种产品的销售包装。 随着运输方式的改变和销售方式的变革,纸箱、纸盒的样式日趋多样化, 几乎每一种新型的非标纸箱都伴随着一套自动化设备问世,而造型新颖的 纸盒本身,也成为了商品促销的手段。 纸箱、纸盒的分类 纸箱和纸盒的种类繁多、型式多样,分类方式也有很多种。 纸箱的分类 最常见的分类是按照纸板的瓦楞楞形来区分的。瓦楞纸板的楞型主 要分为四种: A 楞、B 楞、C 楞和 E 楞。 一般而言,用于外包装的纸箱主要采用 A、B、C 楞型纸板;中包装 采用 B、E 楞型;小包装则多使用 E 楞纸板。 在生产和制造瓦楞纸箱时,一般按纸箱的箱型来进行区分。 瓦楞纸箱的箱型结构,在国际上普遍采用由欧洲瓦楞纸箱制造商联 合会 (FEFCO)和瑞士
《试验设计与统计》着重介绍了环境与资源研究中常见的试验设计和统计分析的基本原理与方法、常用的多元统计分析方法及相应的统计软件应用。
前言
随着科学技术的不断进步,合理地设计试验,正确地分析试验结果,特别是熟练地运用计
算机软件进行试验设计与统计分析,已经成为高素质科技人才的必备技能。本书是特地根据环
境与资源相关专业对试验设计与统计分析方法的要求而编写的。
本书的写作是在作者多年从事试验设计与统计分析的教学和应用研究的基础上完成的。全书共九章,可概括为六部分:第一部分(第一、二章),为试验设计与统计分析的基本原理,主要介绍试验资料的统计描述、统计假设检验的基本原理与各种统计假设检验方法。第二部分
(第三、四章),介绍试验设计和抽样调查的基本原理、类型及方法。第三部分(第五、七章),为各种比较性试验的设计及试验结果统计分析方法,是本书的重点之一,其核心内容是方差分析。第四部分(第六章),为变量之间相互关系的统计分析,主要内容有一元线性回归与相关、多元线性回归、多项式回归、可直线化的曲线回归分析等。第五部分(第八章),简要介绍多元统计分析方法,包括逐步回归分析、通径分析、聚类分析、判别分析、主成分分析、因子分析、典型相关分析和时间序列分析。第六部分(第九章),在介绍运用Excel电子表格数据处理软件进行统计分析的方法和技巧的基础上,重点叙述应用DPS数据处理系统进行试验设计与各种统计分析方法。
书中内容侧重于各种统计方法的应用,在统计原理方面,一般只给出概念的介绍和公式的
简单推导,而避开复杂繁琐的公式推导。有关统计运算方法,本教材不再采用以往教材介绍的
适用于笔算的冗长公式和繁琐的算法,而是介绍思路清晰、方法简单的数据整理和计算器中数
据的输入与输出过程。 目的在于使读者通过本书的学习,掌握试验设计的基本原理与方法,了解有关统计分析方法的原理与适用条件,能熟练地运用ExceZ、DPS数据处理系统等统计软件进行试验设计与统计分析,并对统计结果作出正确的专业解释。
在本书的编写过程中参考了国内外的有关书籍和资料(主要书目列于书后),引用了其中的一些内容和实例,在此,对所有作者和译者表示诚挚的感谢。本书的编写得到了浙江大学教材建设委员会和环境与资源学院领导的大力支持;浙江大学理学院陈叔平教授对本书的编写提出了很多建设性的意见;浙江大学出版社领导和工作人员特别是杜玲玲编辑对本书的出版给予了热情的支持和帮助,在此,一并表示衷心的感谢。
由于编者水平所限,虽经反复修改但错误和不妥之处在所难免,恳请读者批评指正。
方 萍
2003年1月于杭州华家池
第一章 统计学基础知识
第一节 几个常用统计术语
一、总体与样本
二、变数与数据资料
三、参数与统计数
四、误差与错误
五、准确性与精确性
第二节 数据资料的初步整理
第三节 统计特征数
一、表征数据资料集中趋势的统计特征数
二、表征数据资料变异程度的统计特征数
三、常用统计特征数的计算器求算
第四节 概率论基础
一、随机事件与概率
二、概率分布
第五节 抽样分布
一、样本平均数的分布
二、样本平均数差数的分布
三、t分布
四、x2卡方)分布
五、F分布
第二章 统计假设检验
第一节 试验结果的直观分析及其存在问题
一、试验结果直观分析及其存在问题
二、试验数据波动原因
第二节 统计假设检验概述
一、统计假设检验的意义
二、统计假设检验的基本步骤
三、统计假设检验的两类错误
四、双尾检验与单尾检验
五、假设检验应注意的问题
第三节 平均数比较的假设检验
一、单个总体平均数的假设检验
二、两个正态总体平均数比较假设检验
……2100433B
统计量样本矩
设x1,x2,…,xn是一个大小为n的样本,对自然数k,分别称 为k阶样本原
点矩和k阶样本中心矩,统称为样本矩。许多最常用的统计量,都可由样本矩构造。例如,样本均值(即α1)和样本方差 是常用的两个统计量,前者反映总体中心位置的信息,后者反映总体分散情况。还有其他常用的统计量,如样本标准差,样本变异系数S/塣,样本偏度,样本峰度等都是样本矩的函数。若(x1,Y1),(x2,Y2),…,(xn,Yn)是从二维总体(x,Y)抽出的简单样本,则样本协方差·及样本相关系数 也是常用的统计量,r可用于推断x和Y的相关性。
统计量次序统计量
把样本X1,x2,…,xn由小到大排列,得到,称之为样本x1,x2,…
,xn的次序统计量。其中最小次序统计量x⑴最大次序统计量x(n)称为极值,在那些如年枯水量、年最大地震级数、材料的断裂强度等的统计问题中很有用。还有一些由次序统计量派生出来的有用的统计量,如:样本中位数 是总体分布中心位置的一种度量,若样本大小n为奇数,,若n为偶数,,它容易计算且有良好的稳健性。样本p分位数Zp(0<p<1)及极差x(n)-x⑴也是重要的统计量。其中Zp当时即为中位数,而当时,表示不超过1 np的最大整数)。样本分位数的一个重要应用是构造连续总体分布的非参数性容忍区间(见区间估计)。
统计量U统计量
这是W.霍夫丁于1948年引进的,它在非参数统计中有广泛的应用。其定义是:设x1,x2,…,xn,为简单样本,m为不超过n的自然数,为m元对称函数,则称 为样本x1,x2,…,xn的以为核的U统计量。样本均值和样本方差都是它的特例。从霍夫丁开始,这种统计量的大样本性质得到了深入的研究,主要应用于构造非参数性的量的一致最小方差无偏估计(见点估计),并在这种估计的基础上检验非参数性总体中的有关假设。
统计量秩统计量
把样本X1,X2,…,Xn 按大小排列为,若 则称Ri为xi的秩,全部n个秩R1,R2,…,Rn构成秩统计量,它的取值总是1,2,…,n的某个排列。秩统计量是非参数统计的一个主要工具。
还有一些统计量是因其与一定的统计方法的联系而引进的。如假设检验中的似然比原则所导致的似然比统计量,K.皮尔森的拟合优度(见假设检验)准则所导致的Ⅹ统计量,线性统计模型中的最小二乘法所导致的一系列线性与二次型统计量,等等。
- 相关百科
- 相关知识
- 相关专栏
- 统计调查与数据分析
- 统计调查方案
- 统计质量控制图理论与方法
- 统计质量控制法
- 统计质量控制
- 统计软件SPSS完全学习手册与实战精粹
- 统计过程控制(SPC)体系实施指南
- 统计过程控制体系实施指南
- 统计过程控制的策划与实施
- 统计违法违纪行为处分规定
- 统计部门
- 统计需求分析法
- 绣江河拦河分洪工程
- 绥中电厂800MW机组节能环保升级改造创新实践
- 绥中第四建筑工程总公司
- 绥中花岗岩结构与成因研究
- 分形DGS单元结构设计及其在微带电路中的应用
- 逆变TIG焊机接触引弧电路的设计(引弧电路)
- 以MSP430FW427为核心的远程数字水表设计
- 引江济淮工程淠河总干渠以北安徽段截污导流工程设计
- 中华大厦五层宏远公司办公室内装修工程施工组织设计
- 招远电视台制作播出系统数字化改造工程的设计与实践
- 全热回收地源热泵空调机组的系统及工程方案设计
- 展览馆装饰工程消防改造施工组织设计方案(91页)
- 支持群体设计的工程数据库管理系统的结构及实现
- 智能建筑工程设计中的机电设备集成配置系统总体设计
- 中国石化北京设计院标准工艺装置管道垫片选用规定
- 中航格澜阳光花园一期门禁对讲建设项目施工组织设计
- 在书香中沉睡——“川大河畔”高尚住宅小区景观设计
- 高效率PWM/PFM自动切换升压转换器的设计
- 智能小区以太接入交换机SNMP代理设计与实现
- 医用洁净空调系统设计调试中易忽视的问题及设计优化