统计分类目录
统计分类目录是指根据统计调查的需要,对统计客体所作的分类,如行业分类、职业分类、地区分类等,是进行统计调查资料分类整理的依据。
统计分类目录是指统计分类标准的一种,如商品可以按生产单位划分为农副产品、工业产品;按用途可以划分为生产资料和消费资料。消费资料还可按吃、穿、用、烧等进行分类。分类目录是统计调查资料分类整理的依据,是分析研究的基础。统计调查的分类目录必须由国家统一制定。2100433B
统计分类目录造价信息
统计分类目录常见问题
-
也可以参考一下如下分类: 生化仪器 离心机 培养箱 气候箱 摇床 电泳设备 恒温设备 干燥设备 振荡器 匀浆/混合器 搅拌器 制冷设备 各类泵 其他 净化纯水设备 生物安全柜 净化工作台 超...
-
总结归来有5大系列:金属护栏网系列、防护网系列、围墙网系列、异型护栏网系列、新型组装栅栏系列。其中金属护栏网系列包括:框架护栏网、双边丝护栏网、双圈护栏网、挂钩式三角防护网、护栏网片、护栏网配件、护栏...
-
新版软件都可以单独显示剔槽工程量,先识别墙体,并把墙体修改为砌块墙,然后识别管线,软件自动可以显示剔槽工程量。 山东刚性阻燃管包含剔槽补槽,其他不含,第二册有单独子目。
统计分类目录文献

 分类目录汇总
分类目录汇总
关于指定《医疗器械分类目录》的说明 一、《医疗器械分类目录》制定的依据 《医疗器械监督管理条例》 及《医疗器械分类规则》 (第 15号局长令)。 二、《医疗器械分类目录》与《医疗器械分类规则》的关系 《医疗器械分类规则》 用于指导《医疗器械分类目录》 的制定和确定新的产 品注册类别。我国实行的医疗器械分类方法是分类规则指导下的目录分类制, 分 类规则和分类目录并存。一旦分类目录已实施,应执行分类目录。 三、制定分类目录的原则 执行分类规则指导下的目录分类制。 参照国际通行的分类, 从严掌握。使用 风险是制定产品分类目录的基础。 分类目录尽可能适应管理的需要, 有利于理顺监督管理, 做到科学合理。 四、符合医疗器械定义的含药医疗器械为 III 类医疗器械。 五、由于各种手术包内组件不确定, 所以本目录不包含该类产品。 凡手术包 内含有 III 类医疗器械的,作为 III 类产品管理;只含有

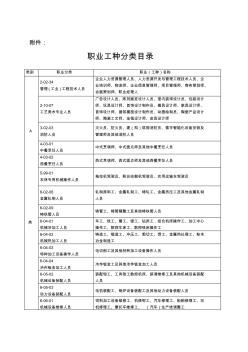 职业工种分类目录
职业工种分类目录
附件: 职业工种分类目录 类别 职业分类 职业(工种)名称 A 类 2-02-34 管理 (工业 )工程技术人员 企业人力资源管理人员、人力资源开发与管理工程技术人员、企 业培训师、物流师、企业信息管理师、项目管理师、商务策划师、 会展策划师、职业经理人 2-10-07 工艺美术专业人员 广告设计人员、陈列展览设计人员、室内装饰设计员、包装设计 师、玩具设计师、首饰设计制作员、模具设计师、家具设计师、 首饰设计师、建筑模型设计制作员、动画绘制员、陶瓷产品设计 师、陶瓷工艺师、地毯设计师、皮具设计师 3-02-03 消防人员 灭火员、防火员、建(构)筑物消防员、楼宇智能化设备安装及 管理师及其他消防人员 4-03-01 中餐烹饪人员 中式烹调师、中式面点师及其他中餐烹饪人员 4-03-02 西餐烹饪人员 西式烹调师、西式面点师及其他西餐烹饪人员 5-99-01 农林专用机械操作
主要包含有以下分类目录:
工程硕士论文 林业工程师论文 电力工程论文 化工工程论文 控制工程论文 工业工程论文 系统工程论文 电气工程论文水利工程论文 工程师职称论文 公路工程论文 软件工程论文 建筑工程论文 土木工程论文 工程类杂志
统计设计是统计工作的首要阶段,是根据统计研究的目的和研究对象的特点,明确统计指标和指标体系,以及对应的分组方法,并以分析方法指导实际的统计活动。其基本任务是制定出各种统计工作方案,是统计工作过程不可缺少的重要环节之一,是统计工作的指导依据。统计设计所制定的方案包括:统计指标体系、统计分类目录、统计报表制度、统计调查方案、统计汇总或整理方案以及统计分析方案等诸多方面的内容。
统计量样本矩
设x1,x2,…,xn是一个大小为n的样本,对自然数k,分别称 为k阶样本原
点矩和k阶样本中心矩,统称为样本矩。许多最常用的统计量,都可由样本矩构造。例如,样本均值(即α1)和样本方差 是常用的两个统计量,前者反映总体中心位置的信息,后者反映总体分散情况。还有其他常用的统计量,如样本标准差,样本变异系数S/塣,样本偏度,样本峰度等都是样本矩的函数。若(x1,Y1),(x2,Y2),…,(xn,Yn)是从二维总体(x,Y)抽出的简单样本,则样本协方差·及样本相关系数 也是常用的统计量,r可用于推断x和Y的相关性。
统计量次序统计量
把样本X1,x2,…,xn由小到大排列,得到,称之为样本x1,x2,…
,xn的次序统计量。其中最小次序统计量x⑴最大次序统计量x(n)称为极值,在那些如年枯水量、年最大地震级数、材料的断裂强度等的统计问题中很有用。还有一些由次序统计量派生出来的有用的统计量,如:样本中位数 是总体分布中心位置的一种度量,若样本大小n为奇数,,若n为偶数,,它容易计算且有良好的稳健性。样本p分位数Zp(0<p<1)及极差x(n)-x⑴也是重要的统计量。其中Zp当时即为中位数,而当时,表示不超过1 np的最大整数)。样本分位数的一个重要应用是构造连续总体分布的非参数性容忍区间(见区间估计)。
统计量U统计量
这是W.霍夫丁于1948年引进的,它在非参数统计中有广泛的应用。其定义是:设x1,x2,…,xn,为简单样本,m为不超过n的自然数,为m元对称函数,则称 为样本x1,x2,…,xn的以为核的U统计量。样本均值和样本方差都是它的特例。从霍夫丁开始,这种统计量的大样本性质得到了深入的研究,主要应用于构造非参数性的量的一致最小方差无偏估计(见点估计),并在这种估计的基础上检验非参数性总体中的有关假设。
统计量秩统计量
把样本X1,X2,…,Xn 按大小排列为,若 则称Ri为xi的秩,全部n个秩R1,R2,…,Rn构成秩统计量,它的取值总是1,2,…,n的某个排列。秩统计量是非参数统计的一个主要工具。
还有一些统计量是因其与一定的统计方法的联系而引进的。如假设检验中的似然比原则所导致的似然比统计量,K.皮尔森的拟合优度(见假设检验)准则所导致的Ⅹ统计量,线性统计模型中的最小二乘法所导致的一系列线性与二次型统计量,等等。
- 相关百科
- 相关知识
- 相关专栏
- 统计分组体系
- 统计制度
- 统计功效
- 统计原始记录
- 统计员岗位专业知识培训试行办法
- 统计员岗位知识与技能
- 统计员
- 统计和数据分析
- 统计噪声级
- 统计基层基础建设经验交流材料汇编
- 统计基础工作管理
- 统计基础知识与统计实务历年真题与过关必做600题详解
- 统计基础知识习题集(第二版)
- 统计基础知识(第四版)
- 统计基础知识
- 统计填表说明
- 中国水利水电地下工程数据统计
- 元江县统计局行政效能建设工作总结
- 关于做好国有资产评估项目统计工作通知
- 机械设备统计信息工作在施工企业建设中发展趋势分析
- 两排和多排风口冲天炉用铸造焦熔炼效果数理统计
- 基于多元统计引黄水库沉沙条渠泥沙与水质变异分析
- 建筑工程材料、成品、半成品场内运输和操作损耗统计表
- 建筑工程材料、成品、半成品场内运输及操作损耗统计表
- 交通运输安全生产事故统计报表制度
- 分类目录深圳市建筑工程文件归档内容业务指引
- 建筑工程统计表给水管道系统通水试验记录
- 基于事故统计分析城市轨道交通运营安全和可靠性
- 基于统计分析粉土区域变化规律及其物理力学性质
- 基于多元统计分析石头口门水库汇水流域水质综合评价
- 清远市混凝土原材料砂质量检测情况统计
- 电土施表混凝土试块强度统计、评定记录表