弹性分析
弹性分析基本信息
| 中文名 | 弹性分析 | 外文名 | elastic analysis |
|---|---|---|---|
| 所属学科 | 建筑学 | 公布时间 | 2014年 |
《建筑学名词》第二版。 2100433B
弹性分析造价信息
基于线性应力–应变或弯矩–曲率关系,采用弹性理论分析方法对初始结构几何形体进行的结构分析。
弹性分析常见问题
-
弹性腻子主要是用来找补墙面缝隙,由于它有一定的张力,在墙面缝隙在受温度/湿度/外力等影响,而随之改变,墙面不会出现缝隙。但是超过一定限度还会出现缝隙。“弹性”的含义就是有一定的张力。
-
弹性腻子采用丙烯酸乳液与无机材料复合而成,用于解决建筑墙体饰面龟裂的质量问题。使用于各种墙体饰面的抗微裂基层处理,包括混凝土、水泥砂浆抹面、空心砌砖及各类保温板饰面。按弹性高低分,分为高弹、中弹、低弹...
-
弹性漆又称橡胶漆、类肤漆,是一种手感漆常用于经常接触的物件表面给人以柔和的质感,是现在流行的一种油漆。常用于建筑外墙涂料。下面简单介绍弹性漆的配方及其原理。油漆配方示例A组分:二 30丁酯 30二醇 ...
弹性分析文献

 粘弹性桩的混沌运动分析
粘弹性桩的混沌运动分析
粘弹性桩的混沌运动分析——研究了在轴向载荷和周期性横向载荷共同作用下非线性粘弹性嵌岩桩的混沌运动情况。假定桩和土体分别满足Leaderman非线性粘弹性和线性粘弹性本构关系,得到的运动方程为非线性偏微分.积分方程;利用Ga|erkin方法将方程简化为非线性常...
供给弹性定性分析
供给弹性,与需求价 格弹性类似,是指一种商品市场价格的相对变动所引起的供给量的相对变动,即供给量的变化率与价格变化率的比值。亦即供给量变动对价格变动的反应程度。供给价格弹性是用来衡量商品的供给量变动对商品自身价格变动反应灵敏程度的。
当△P→0时:
(一)线性供给价格弹性
1.凡通过原点的线性供给曲线,由于供给量的变化率都等于价格的变化率,任何点弹性或弧弹性均为单一弹性。S1上的点弹性为:
E、F两点之间的弧弹性为:
同理,可以求得供给曲线S2上任何点的弹性均为1。
2.凡通过原点右边(与横轴相交)的供给曲线,均为缺乏弹性。
点E:
(因为BA<OA)
3.凡通过原点左边(与纵轴相交)的供给曲线,均为富有弹性。
S1的E点:
(因CA>OA)
(二)非线性供给价格弹性
如果供给曲线为非线性,则可根据弹性测定点的切线是否通过原点和通过原点的右边还是左边,来判定该点弹性的大小,其计算方法同线性供给曲线。
表现
供给规律表明,价格上升供给量增加。供给价格弹性衡量供给量对价格变动的反应程度。如果供给量对价格变动的反应很大,可以说这种物品的供给是富有弹性的,反之,供给是缺乏弹性的。
供给价格弹性取决于卖者改变他们生产的物品产量的伸缩性,例如,海滩土地供给缺乏弹性是因为几乎不可能生产出土地,相反书,汽车这类制成品供给富有弹性。
大多数市场上,供给价格弹性关键的决定因素是所考虑的时间长短。在长期中的弹性通常都大于短期。在短期中,企业不能轻易地改变工厂规模来增加或减少一种物品的生产。在长期中,企业可以建立新工厂或关闭旧工厂,此外,新企业可以进入一个市场而旧企业可以关门,因此在长期供给中供给量可以对价格作出相当大的反应。
计算供给价格弹性:
供给价格弹性=供给量变动百分比 / 价格变动百分比
由于企业通常有最大生产能力,所以在供给量非常低时,供给弹性会非常高,而在供给量水平高时,供给弹性又会非常低。
种类
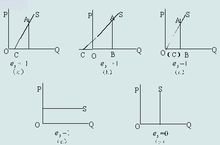
供给的价格弹性可以根据es值的大小分为五种类型。es>1表示供给富于弹性;es<1表示供给缺乏弹性;es=1表示供给单一弹性或单位弹性;es=∞表示供给完全弹性;es=0表示供给完全无弹性。
现实经济生活中,供给单一弹性、供给完全无弹性和供给完全富于弹性比较少见,大多数商品的供给不是富于弹性就是缺乏弹性。如一些不可再生性资源如土地的供给,以及那些无法复制的珍品的供给价格弹性等于零,而在劳动力严重过剩地区劳动力供给曲线具有完全弹性(无穷大弹性)的特点。
供给的价格点弹性可以用公式直接计算得出,也可以用几何方法来求出。假定供给函数是非线性的,如图所示,供给曲线上任一点A的点弹性可表示为线段CB与线段OB之比值,S为A点的切线。即A点的点弹性
从图中可以看出,如果A点的切线S在原点的的右端与横坐标相交于C点,则线段CB小于线段OB,即说明A点的点弹性小于1;如果A′点的切线S′在原点的左端与横坐标相交(如图的A′点),则线段C′B′大于线段OB′,即说明A′点的点弹性大于一。所以,可以得出一般结论:
①若供给曲线上任一点的切线在原点的右端交于横坐标,则在该点有es<1;
②若供给曲线上任一点的切线在原点的左端交于横坐标,则在该点有es>1;
③若供给曲线上任一点 切线过原点,则在该点有es­=1。
可见,在供给函数为非线性的情况下,曲线上各点的弹性是不同的。如果供给函数是线性的(只要供给曲线不是向右下倾斜),则供给线上各点的弹性是相同的,其几何意义非常直观。即只要线性的供给曲线在原点的右端交于横坐标,那么整条供给曲线上供给价格弹性都小于1;如果线性供给曲线在原点左端交于横坐标,那么整条曲线上供给价格弹性都大于1;若线性的供给曲线过原点,则整条供给曲线上供给价格弹性都等于1。
因素
供给取决于生产。
1、生产时期的长短。在短期内,生产设备、劳动等生产要素无法大幅度增加,从而供给无法大量增加,供给弹性也就小。尤其在特短期内,供给只能由存货来调节,供给弹性几乎是零。在长期中,生产能力可以提高,因此供给弹性也就大。这是影响供给弹性大小的最重要的因素。
2、生产的难易程度。一般而言,容易生产而且生产周期短的产品对价格变动的反应快,其供给弹性大。反之,生产不易且生产周期长的产品对价格变动的反应慢,其供给弹性也就小。
3、生产要素的供给弹性。供给取决于生产要素的供给。因此,生产要素的供给弹性大,产品供给弹性也大。反之,生产要素的供给弹性小,产品供给弹性也小。
4、生产所采用的技术类型。有些生产采用资本密集型技术。这些产品的生产规模一旦固定,变动就较难,从而其供给弹性也小;有些产品采用劳动密集型技术。这些产品的生存规模变动较容易,从而其供给弹性也就大。
地基梁被广泛的应用于工业与民用建筑中,例如建筑物的条形基础、格式梁基础等以及地道桥等构筑物,都可作为地基上的梁来进行计算。在地基梁的计算中,必须考虑地基梁与地基之间的相互作用。地基梁和地基相互作用问题属于接触问题范畴,如果假设地基是弹性的,这类基础梁就称为弹性地基梁。在计算弹性地基梁时,重要的问题是如何确定地基反力与地基沉降之间的关系,也就是如何选取地基模型的问题。计算弹性地基梁时或进行弹性地基梁分析,不论基于何种地基模型假定,都要满足两个基本求解条件:1) 地基和地基梁之间的变形协调条件,即地基和地基梁在计算前后必须保持接触,不得出现分离的现象;2) 满足静力平衡条件,即地基梁在外荷载和基底反力共同作用下必须处于静力平衡状态。
对于弹性地基上的梁的问题,许多的学者进行了深入的研究,并且提出了多种反映土体对梁作用的模型。他们的研究可以分为两类:一类是基于弹性半空间理论模型,另一类是基于文克尔假设模型。弹性半空间模型假定地基为一个连续均匀的弹性体,而文克尔模型用一系列具有固定刚度的弹簧来模拟地基,且假定梁下某点的地基反力与该点的挠度成正比 。
弹性半空间地基模型是将地基看成是均质的、各向同性的弹性半无限体。为了充分评价冲刷对桥墩及桥梁整体稳定性的影响, 应用弹性半空间地基模型分别对在各种不同冲刷程度影响下的桥墩各项检算内容进行了最不利原则计算分析。此时, 分析荷载组合考虑为主力加附加力, 且只考虑主力与顺桥方向的附加力相结合。在计算分析基底压应力时, 以2孔重载为计算荷载;在计算分析墩顶弹性水平位移时, 以1孔重载为计算荷载。最不利情况下的地基模型模拟基底淘空的方法是将基底冲刷淘空形状稍偏于安全的取为以矩形基底长边为固定底边的三角形。
谈弹性半空间地基模型冲刷对墩顶弹性水平位移的影响分析
墩顶弹性水平位移由两部分组成, 一部分是由于桥墩挠曲变形引起的位移Δ1 , 另一部分是地基土变形引起的位移Δ2 , 总位移为两者的叠加即
Δ =Δ1 Δ2
计算Δ1 时, 视桥墩墩顶为自由、墩底为固定的悬臂梁, 由于墩身为变截面, 通过Matlab编程利用积分进行计算。Δ2 是由地基土的不均匀沉降引起的位移。由于受冲刷的影响, 墩底地基被部分淘空会引起墩身的倾覆, 从而威胁桥墩的稳定, 其地基不均匀沉降的计算也不同于常规方法。
3个墩墩顶弹性水平位移规范容许值分别为27.2 mm、38.9 mm、27.2 mm, 对应的极限冲刷淘空面积占基底总面积百分比分别为20.7%、32.9%、17.8%。
谈弹性半空间地基模型冲刷对基底压应力的影响分析
随着冲刷的不断加剧, 淘空部分地基失去承载能力, 并引起基础中性轴位置的改变, 应力重新分布。由程序计算结果得出冲刷淘空面积占基底总面积的百分比与基底最大压应力的拟合曲线表达式分别为
σ =(2.735 1x2 2.249 4x 0.382 5)×103(6)
σ =(2.904 0x2 2.334 5x 0.395 5)×103(7)
σ =(2.817 7x2 2.300 4x 0.390 7)×103(8)
式中, x为冲刷淘空面积占基底总面积的百分比;σ为桥墩相应冲刷淘空情况下的基底最大压应力。当冲刷面积达26.0%、24.8%、25.3%以后, 最大基底压应力大于1.2 , 基底承载力不再满足要求。
根据以上的分析计算, 得出各桥墩在各种不同冲刷情况下的基底最大压应力、墩顶弹性水平位移(纵向)曲线图。其中, 4 号墩受冲刷的影响最为严重:当其余两个桥墩仍然可以安全工作时, 4号墩的墩顶弹性水平位移则濒临危险值。在水下探测时发现, 4 号桥墩处水流湍急, 冲刷较另外两个桥墩严重, 因此应及时对其进行加固、防护等处理。
基底最大压应力随冲刷淘空面积的增加而增大, 基底最大压应力增加的幅度也越来越大, 曲线的走向越来越陡。当冲刷淘空面积占基底面积的25%附近时, σmax=973.79 kPa, 已经接近于其容许应力[ σ] =1 080 kPa。
与基底最大压应力的分析结果相似, 4 号桥墩的纵向墩顶弹性水平位移也有着相似的走势。随着冲刷淘空面积的增加, 纵向墩顶弹性水平位移增加的幅度也越来越大, 位移值越来越大。当冲刷淘空部分的面积达到基底面积的17.8%左右时, 墩顶弹性水平位移值已经超出了最大容许位移值。据此曲线分析, 当冲刷淘空面积接近基底面积的18%时,该墩墩顶弹性水平位移值达到最大容许位移值 。
- 相关百科
- 相关知识
- 相关专栏
- 弹性力学与有限元法教程
- 弹性力学与有限元
- 弹性力学及其在岩土工程中的应用
- 《弹性力学》2009版图书
- 弹性力学
- 弹性半空间地基假设
- 弹性地基板
- 弹性地基梁比拟法
- 弹性支座
- 弹性支承块式无砟轨道部件第4部分块下垫板
- 弹性支承连续梁法
- 弹性波勘探测试
- 弹石路面建设与养护
- 弹石路面设计施工技术指南
- 弹簧托梁
- 弹簧模具
- 中国吹制玻璃行业市场前景分析预测年度报告(目录)
- 中国电力井盖行业市场前景分析预测年度报告(目录)
- 中国轨道射灯行业市场前景分析预测年度报告
- 智能磨音频谱分析仪(DF-6811A)使用说明书
- 园林绿化养护精细化管理对河源市园林景观的影响分析
- 中国民宿消费市场格局分析及十三五发展环境分析报告
- 圆CFRP-钢管混凝土偏压构件荷载-变形关系分析
- 云计算对企业信息化系统建设和运营的影响分析和改进
- 中国仿古青砖行业市场前景分析预测年度报告(目录)
- 在8度地震区建造低层纯钢框架结构住宅的可行性分析
- 中国家具钢管行业市场前景分析预测年度报告(目录)
- 中国电动汽车充电站市场现状与投资分析报告
- 云南璟成工程项目管理有限公司-招投标数据分析报告
- 影响水利工程质量监督职能发挥的主要因素及对策分析
- 杂散电容对交流法微电容测量电路噪声特性影响的分析
- 引黄济临供水工程一级泵站圆形筒体支护结构计算分析

