Szilassi多面体顶点坐标
当一Szilassi多面体的最短边长为一、重心位于原点时,此时14顶点分别为:
Szilassi多面体造价信息
如图2所示:
如图册1所示:
Szilassi多面体顶点坐标常见问题
-
你可以先假设球体的半径为R,则球的内接多面体中正多面体的长宽高皆为根号R ,故球的内接多面体中正多面体的体积为2*R立方*根号2。
-
-b 4ac-b*bx=-------- y=---------- 2a 4a
-
抛物线顶点坐标公式:当h>0时,y=a(x-h)2的图象可由抛物线y=ax²;向右平行移动h个单位得到,当h<0时,则向左平行移动|h|个单位得到.当h>0,k>0时...
Szilassi多面体顶点坐标文献

 异形多面体钢屋盖结构施工成套技术
异形多面体钢屋盖结构施工成套技术
针对异形多面体钢屋盖结构的施工难题提出一系列施工成套技术,发明了\"异形构件的虚拟四面体顶点测量定位方法\

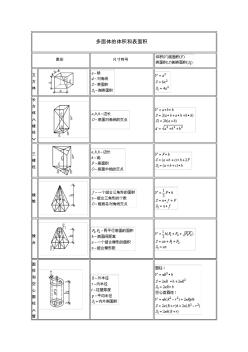 施工员计算公式大全(多面体的体积和表面积)
施工员计算公式大全(多面体的体积和表面积)
多面体的体积和表面积 图形 尺寸符号 立 方 体 长 方 体 ∧ 棱 柱 ∨ 三 棱 柱 棱 锥 棱 台 圆 柱 和 空 心 圆 柱 ∧ 管 ∨ 斜 线 直 圆 柱 直 圆 锥 圆 台 球 球 扇 形 ∧ 球 楔 ∨ 球 缺 圆 环 体 ∧ 胎 ∨ 球 带 体 桶 形 椭 球 体 a,b,c-半轴 交 叉 圆 柱 体 梯 形 体 常用图形求面积公式 图形 尺寸符号 面积( F) 表面积( S) 正 方 形 长 方 形 三 角 形 平 行 四 边 形 任 意 四 边 形 正 多 边 形 菱 形 梯 形 圆 形 椭 圆 形 a·b-主轴 F= ( π /4) a ·b 扇 形 弓 形 圆 环 部 分 圆 环 新 月 形 L d/10 2d/10 3d/10 4d/10 5d/10 6d/10 7d/10 P 0.40 0.79 1.18 1.56 1.91 2.25 2.55 抛 物 线 形
正多面体,或称柏拉图立体, 指各面都是全等的正多边形且每一个顶点所接的面数都是一样的凸多面体。因此对于每两个顶点来说都有一个等距的映射将其中一点映射到另一点。
命名由来
正多面体的别称柏拉图立体是因柏拉图而命名的。柏拉图的朋友特埃特图斯告诉柏拉图这些立体,柏拉图便将这些立体写在《提玛友斯》内。正多面体的作法收录《几何原本》的第13卷。在命题13描述正四面体的作法,命题14就是正八面体,命题15为立方体,命题16是正二十面体,命题17是正十二面体。
判断依据
判断正多面体的依据有三条:
(1)正多面体的面由正多边形构成
(2)正多面体的各个顶角相等
(3)正多面体的各条棱长都相等
这三个条件都必须同时满足,否则就不是正多面体,比如五角十二面体,虽然和正十二面体一样是由十二个五角形围成的,但是由于它的各个顶角并不相等因此不是正多面体。
正多边形都是轴对称图形,正偶数边形既是轴对称图形又是中心对称图形 如果 n 是偶数,则这些轴线中有一半经过相对的顶点,另外一半经过相对边的中点。如果 n 是奇数,则所有的轴线都是经过一个顶点以及其相对边的中心。例如:正多边形的周长与它的外接圆的直径的比值,与直径长短无关。古代数学家正是利用这一性质,逐次倍增正多边形的边数,使正多边形的周长趋近它的外接圆的周长,从而求得了圆周率的近似值。
在经典意义上,一个多面体(polyhedron) (英语词来自希腊语 πολυεδρον,poly-,就是词根πολυς, 代表"多", + -edron,来自εδρον,代表"基底","座",或者"面")是一个三维形体,它由有限个多边形面组成,每个面都是某个平面的一部分,面相交于边,每条边是直线段,而边交于点,称为顶点。立方体,棱锥和棱柱都是多面体的例子。多面体包住三维空间的一块有界体积;有时内部的体也视为多面体的一部分。一个多面体是多边形的三维对应。多边形,多面体和更高维的对应物的一般术语是多胞体。
正多面体 所谓正多面体,是指多面体的各个面都是全等的正多边形,并且各个多面角都是全等的多面角。例如,正四面体(即正棱锥体)的四个面都是全等的三角形,每个顶点有一个三面角,共有三个三面角,可以完全重合,也就是说它们是全等的。
正多面体的种数很少。多面体可以有无数,但正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体五种。其中面数最少的是正四面体,面数最多的是正二十面体。有些化学元素的结晶体呈正多面体的形状,如食盐的结晶体是正六面体,明矾的结晶体是正八面体。
古希腊的毕达哥拉斯学派曾对五种小多面体作过专门研究,并将研究成果拿到柏拉顿学校教授。故而,西方数学界也将这五种正多面体称为柏拉顿立体。
类型 | 面数 | 棱数 | 顶点数 | 每面边数 | 每顶点棱数 |
正4面体 | 4 | 6 | 4 | 3 | 3 |
正6面体 | 6 | 12 | 8 | 4 | 3 |
正8面体 | 8 | 12 | 6 | 3 | 4 |
正12面体 | 12 | 30 | 20 | 5 | 3 |
正20面体 | 20 | 30 | 12 | 3 | 5 |
多面体要素
多面体要素是一种可存储面集合的GIS 对象,能够在数据库中将 3D 对象的边界表示为单个行。面可存储表示要素组成部分的纹理、颜色、透明度和几何信息。面中存储的几何信息可以是三角形、三角扇、三角条带或环。
所有多面体都将 z 值作为用于构建面的坐标系的一部分而存储。尽管可以使用数字要素属性建立多面体的基础 z值模型,但此选项可能不支持使用嵌入式 z 值时可用的相同分析和交互选项。
有些多面体要素被视为已闭合,这表示它们正确定义了体积。闭合的多面体可用于其他分析工具,如 3D 联合和 3D相交。要将多面体视为已闭合,必须以正确方式构造该多面体。要素必须代表一个相异的体积。构成该体积的面必须具有与其坐标相同的逆时针方向并参与定义体积的外壳。这些面不得彼此相交,并且壳中不得存在间距或空白空间。可以使用是否为闭合地理处理工具来验证多面体是否已正确闭合。
多面体要素的示例包括带纹理的建筑物、灯柱、树、子表面地层、地下建筑物或某种类型的分析表面。
创建多面体要素类
要创建新的多面体要素类,只需在定义要素类的几何时从类型下拉菜单中选择"多面体要素"。
z值
Z 值用于表示多面体要素的形状和高程。它可以表示绝对高度或相对于地面的高度。对生成的 3D 要素类进行显示和分析时,两种方法均完全受支持。
应该在要素类所在的要素数据集(如果存在)或在要素类自身(如果没有要素数据集)中定义要素类 z 值的单位和基准面。如果未定义单位,ArcGIS 将假定 z 的单位与 x,y 的单位匹配。此假定可能会带来问题,尤其当 x,y 的单位是地理单位(纬度-经度)时。
创建多面体要素
使用地理处理工具将现有 3D 模型导入到 ArcGIS 中可创建多面体要素。3D 图层到要素类地理处理工具会将通过各种模型格式(如 SketchUp、OpenFlight、3ds 或 COLLADA)符号化的点转换为多面体要素类。导入 3D 文件地理处理工具也可执行相同操作,但会提供更多导入格式选项(如 VRML)。此外,也可使用 ArcObjects 以程序的方式来构造多面体要素。
- 相关百科
- 相关知识
- 相关专栏
- SZZCYM磁力抛光机
- T型槽单围平板
- T型槽定盘
- T型槽平台
- T型槽平板弯板
- T恤万能打印机
- T恤印刷机
- T恤打印机
- T恤数码打印机
- T恤服装打印机
- T系列螺旋伞齿轮转向器
- T系列螺旋转向箱
- T系列螺旋锥齿轮换向器
- T系列转向箱
- T+0
- T/C面料
- 在公路互通式立交设计中用解析法编程计算楔形端坐标
- 关于铁路曲线桥梁墩台支座垫石中心坐标计算方法
- 基于LonWorks总线遥测双向垂线坐标仪设计
- 广州地铁3号线盾构始发井洞门环中心三维坐标测量技术
- 利用JSCORS技术实现区域水利工程坐标系统统一
- 利用静态GPS测量数据进行RTK坐标转换方法
- 利用Excel编程计算路桥高精度坐标和方位角
- 基于椭球膨胀法建立独立坐标系在工程中应用
- 三维坐标法在江阴长江公路大桥南塔施工测量控制中的应用
- 平面直角坐标系全章复习与巩固提高知识讲解
- 引黄入晋施工测量技术辐射投影及不同高程面坐标变换
- 国家游泳中心工程新型多面体空间刚架钢结构安装方案设想
- VB的数学测量坐标系统转换程序设计与实现
- Pro/E3D模型的圆柱凸轮廓面三坐标测量
- 机载激光测量技术在大区域工程应用中的坐标转换问题
- 坐标系转换参数对实时动态测量(RTK)精度的影响