塑性截面抵抗矩基本信息
| 中文名 | 塑性截面抵抗矩 | 外文名 | Plastic Modulus |
|---|---|---|---|
| 别 名 | 受弯塑性抵抗矩 | 表达式 | Wpl |
| 适用领域 | 土木工程 | 应用学科 | 土木工程 |
截面塑性抵抗矩Wpx。
1)找出达到极限弯矩时截面的中和轴。它是与弯矩主轴平行的截面面积平分线,该中和轴两边的面积相等。在双轴对称截面中,这条轴是主轴。
2)分别求两侧面积对中和轴的面积矩,面积矩之和即为塑性截面模量。2100433B
塑性截面抵抗矩造价信息
塑性截面抵抗矩常见问题
-
截面抵抗矩(W)就是截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值。工程实际中最常见的弯曲问题是横力弯曲,横截面上不仅有正应力,而且还有切应力。由于切应力的作用,横截面发生翘曲,平面假设不再成立...
-
截面抵抗矩 就是截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值。工程实际中最常见的弯曲问题是横力弯曲,横截面上不仅有正应力,而且还有切应力。由于切应力的作用,横截面发生翘曲,平面假设不再成立。但...
-
截面抵抗矩:一种是塑性截面抵抗矩(塑性设计时采用),一种是弹性截面抵抗矩(弹性设计时采用)。截面抵抗矩是截面本身所具有的特性,与外力无关,所以要用W=2Ix/h计算,当然这个公式也只是适用于对...
塑性截面抵抗矩文献

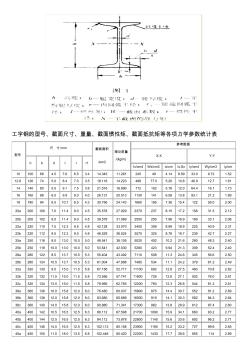 工字钢和槽钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表
工字钢和槽钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表
工字钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表 型号 尺 寸 /mm 截面面积 /em2 理论质量 /(kg/m) 参考数值 X-X Y-Y h b d t r r1 1x/cm4 Wx/cm3 ix/cm Ix:Sx Iy/cm4 Wy/cm3 iy/cm 10 100 68 4.5 7.6 6.5 3.4 14.345 11.261 245 49 4.14 8.59 33.0 9.72 1.52 12.6 126 74 5.0 8.4 7.0 3.5 18.118 14.223 488 77.5 5.20 10.8 46.9 12.7 1.61 14 140 80 5.5 9.1 7.5 3.8 21.516 16.890 712 102 5.76 12.0 64.4 16.1 1.73 16 160 88 6.0 9.9 8.0 4.0 26

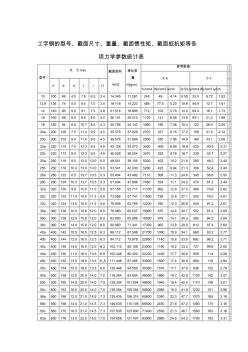 工字钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表
工字钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表
工字钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各 项力学参数统计表 型号 尺 寸 /mm 截面面积 /em2 理论质 量 /(kg/m) 参考数值 X-X Y-Y h b d t r r1 1x/cm4 Wx/cm3 ix/cm Ix:Sx Iy/cm4 Wy/cm3 iy/cm 10 100 68 4.5 7.6 6.5 3.4 14.345 11.261 245 49 4.14 8.59 33.0 9.72 1.52 12.6 126 74 5.0 8.4 7.0 3.5 18.118 14.223 488 77.5 5.20 10.8 46.9 12.7 1.61 14 140 80 5.5 9.1 7.5 3.8 21.516 16.890 712 102 5.76 12.0 64.4 16.1 1.73 16 160 88 6.0 9.9 8.0 4.
矩形截面抵抗矩:
圆形截面的抵抗矩:抗弯时
圆环截面抵抗矩:抗弯时
1)找出达到极限弯矩时截面的中和轴。
中和轴分为弹性中和轴和塑性中和轴;
弹性状态下的中和轴:整个截面关于经此轴线的截面面积矩为0。横截面在此轴线弯曲正应力为0。
截面面积矩:指弹性状态下截面各微元面积与各微元至中和轴距离乘积的积分。单位mm。指弹性状态下中和轴一侧截面的面积矩,主要用于计算截面上任意点的剪切应力值。
塑性状态下的中和轴:塑性中和轴为构件截面面积平分线,该中和轴两边的面积相等。
2)
弹性状态下截面抵抗矩:如本文开头定义。其意义在于在弹性状态下计算某一构件断面位置最不利位置的最大应力,该位置应力满足则此位置截面满足计算要求;
塑性状态下截面塑性抵抗矩:分别求两侧面积对中和轴的面积矩,面积矩之和即为塑性截面模量,也称为塑性抵抗矩。
弹塑件力学是固体力学的重要分支学科。固体材料往往同时具有弹性和塑性性质,特别是材料处在塑性阶段时,变形中既有可恢复的弹性变形,又有不可恢复的塑性变形。
大多数固体材料往往同时具有弹性和塑性性质,因此又常被称为弹塑性材料。弹塑性指的是物体在外力作用下会发生变形,而外力卸载之后变形不一定能完全恢复的性质,其中变形中可恢复部分称为弹性变形,不可恢复部分称为塑性变形。
弹性力学讨论固体材料中的理想弹性体及同体材料弹性变形阶段的力学问题,包括在外力作用下弹性物体的内力、应力、应变和位移的分布,以及与之相关的基础理论。
塑性力学讨论固体材料中塑性阶段的力学问题,采用宏观连续介质力学的研究方法,从材料的宏观塑性行为中抽象出力学模型,并建立相应的数学方程予以描述。可变形同体的弹性阶段与塑性阶段是整个变形过程中的两个不同阶段,弹塑性力学是研究这两个密切相连阶段力学问题的科学。
弹塑性力学经过一百多年的发展,具有一套较完善的理论和方法。随着现代科技的高速发展,研究弹塑性力学新的理论、方法及其在基础工程上的应用尤显重要。塑性力学与弹性力学有着密切的关系,弹性力学中的大部分基本概念和处理问题的方法都可以在塑性力学中得到应用。
弹性力学与塑性力学的根本区别在于弹性力学是以应力和应变呈线性关系的广义Hooke定律为基础。一般来说,在塑性力学的范围中,应力和应变之间的关系呈非线性,而这种非线性的特征与所研究的具体材料有关,对于不同的材料和条件,具有不同的变化规律。
工程材料在应力超过弹性极限以后并未发生破坏,仍具有一定继续承受载荷的能力,但刚度相对地降低,故以弹性力学为基础的没计方法不能充分发挥材料的潜力,某种程度上导致材料的浪费。因此,以塑性力学为基础的设计方法比弹性力学为基础的设计更为优越,更符合实际工程应用。 2100433B
- 相关百科
- 相关知识
- 相关专栏
- 塑性流幅
- 塑性铰线
- 塑料·燃烧性能的测定·水平法和垂直法
- 塑料—拉伸性能的测定第1部分:总则
- 塑料、五金经典模具设计与图例分析
- 塑料光纤槽道规范
- 塑料冷焊接工艺评定
- 塑料制品成型工艺
- 塑料及PVC鞋材中9种限用染料检测液相色谱法
- 塑料增塑剂迁移的测定
- 塑料大棚园艺
- 塑料大棚园艺 | 2版
- 塑料家具中有害物质限量
- 塑料家具通用技术条件
- 塑料工程师手册
- 塑料工程师设计数据手册
- 岳城水库大副坝防渗墙塑性混凝土施工工艺及质量控制
- 圆形截面钢筋混凝土受弯构件正截面承载力的简化计算
- 圆形钢筋混凝土截面大偏压构件正截面承载力的简算法
- 一座变截面连续箱梁桥的腹板斜截面抗剪加固方案
- 中、美混凝土结构设计规范正截面受弯承载力计算对比
- 公称压力PN表示螺栓连接阀盖楔式闸阀力矩参考表
- 基于S3C2440和嵌入式Linux矩阵键盘设计
- 合肥工业大学附属中学教学楼设计内力组合八截面设计
- 厚壁冷弯方矩管和热轧H型钢轴压极限承载力对比
- 基于ANSYS轿车轮毂轴承内法兰盘力矩刚性分析
- 关于混凝土增大截面法在碧州大桥桥梁维修加固工程应用
- 截面尺寸误差对混凝土框架节点抗震性能影响试验
- 某超限高层工业框架结构弹塑性分析及性能抗震加固设计
- 客运专线支架法分段现浇大跨度变截面连续箱梁施工技术
- 基于MIDAS_Gen型钢混凝土结构静力弹塑性分析
- 基于直接转矩变频调速技术智能高层电梯控制系统设计