溶液的弹性相 r于散射,当散射质点〔溶质分子)的尺寸远小于入射光的波长 时,散射强度的空间分布是对称的;然而,当溶质分子的尺寸 与入射光的波长可以比拟时,分子作为一个整体其前后向散 射光的光程差不同,发生内干涉的结果是后向散射光强的减 弱多于前向散射,即前向散射光强大于后向散射光强,呈现出 散射光强的不对称分布。最早这种散射的不对称性是Mie 在研究胶体溶液时发现的,并从实验和理论上分析了这种现 象。提出解释和处理方法,所以大尺寸粒子的散射又被称为 A}ie散射。
散射不对称性造价信息
散射不对称性常见问题
散射不对称性文献

 多回并联电缆线路参数的不对称性分析
多回并联电缆线路参数的不对称性分析
输电线路参数的不对称性对电网的安全运行有着重要影响。为分析并联电缆线路参数的不对称性,首先以卡松线路模型为基础,建立电缆序阻抗参数的计算模型,将高压单芯电缆的金属护套视作普通线路,与大地构成"护套-大地"回路,进而推广到多回并联运行的电缆线路,并阐述了多回电缆序阻抗参数的计算方法;然后通过引入线路参数不平衡度的概念,重点对比分析了几种典型相序排列方式下并联双回电缆线路序阻抗参数的不对称性。分析结果表明:双回并联电缆导线"品"字型排列的对称性优于垂直排列和水平排列,其中又以"品"字型垂直排列的对称性最佳。

 日本当代建筑中的不对称性与非实体性
日本当代建筑中的不对称性与非实体性
在日本传统艺术中,无论是绘画还是建筑都表现着一种特有的不对称与非实体性。这一特征是当代日本建筑中仍有体现,通过分析当今日本有一定影响力的作品,指出不对称性与非实体性存在的必要性,并从理论上总结了其内在的规律。
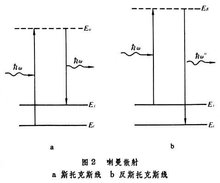
光的散射拉曼散射和布里渊散射
入射光与介质的分子运动间相互作用而引起的频率发生改变的散射。1928年C.拉曼在液 体和气体中观察到散射光频率发生改变的现象,称拉曼效应或拉曼散射。拉曼散射遵守如下规律:散射光中在原始入射谱线(频率为ω0)两侧对称地伴有频率为ω0±ωi(i=1,2,3,…)的一组谱线,长波一侧的谱线称红伴线或斯托克斯线,短波一侧的谱线称紫伴线或反斯托克斯线,统称拉曼谱线;频率差ωi与入射光频率ω0无关,仅由散射物质的性质决定。每种物质都有自己特有的拉曼谱线,常与物质的红外吸收谱相吻合。在经典理论的解释中,介质分子以固有频率ωi振动,与频率为ω0的入射光耦合后产生ω0、ω0-ωi和ω0+ωi三种频率的振动,频率为ω0的振动辐射瑞利散射光,后两种频率对应斯托克斯线和反斯托克斯线。拉曼散射的诠释需用量子力学,不仅可解释散射光的频移,还能解决诸如强度和偏振等问题。
按量子力学,晶体中原子的固有振动能量是量子化的,所有原子振动形成的格波也是量子化的,称为声子。拉曼散射和布里渊散射都是入射光子与声子的非弹性碰撞结果。晶格振动分频率较高的光学支和频率较低的声学支,前者参与的散射是拉曼散射,后者参与的散射是布里渊散射。固体中的各种缺陷、杂质等只要能引起极化率变化的元激发均能产生光的散射过程,称广义的拉曼散射。按习惯频移波数在50-1,000/厘米间为拉曼散射,在0.1-2/厘米间是布里渊散射。
米氏散射(Mie scattering)
I(λ) scattering∝I(λ)incident/λ
米氏发表了任何尺寸均匀球形粒子散射问题的严格解,具有极大的实用价值,可以研究雾、云、日冕、胶体和金属悬浮液的散射等。
当大气中粒子的直径与辐射的波长相当时发生的散射称为米氏散射。
这种散射主要由大气中的微粒,如烟、尘埃、小水滴及气溶胶等引起。米氏散射的辐射强度与波长的二次方成反比,散射在光线向前的方向比向后的方向更强,方向性比较明显。如云雾的粒子大小与红外线(0.7615um)的波长接近,所以云雾对红外线的辐射主要是米氏散射。是故,多云潮湿的天气对米氏散射的影响较大
散射光的波长与入射光相同,而其强度与波长λ成反比的散射,称瑞利散射定律,由瑞利于1871年提出。此定律成立的条件是散射微粒的线度小于波长。若入射光为自然光,不同方向散射光的强度正比于1+cosθ,θ为散射光与入射光间的夹角,称散射角。θ=0或π时散射光仍为自然光;θ=π/2时散射光为线偏振光;在其他方向上则为部分偏振光。根据瑞利散射定律可解释天空的蔚蓝色和夕阳的橙红色。
当散射微粒的线度大于波长时,瑞利散射定律不再成立,散射光强度与微粒的大小和形状有复杂的关系。G.米和P.德拜分别于1908年和1909年以球形粒子为模型详细计算3对电磁波的散射。米氏散射理论表明,当球形粒子的半径a<0.3λ/-2π时散射光强遵守瑞利定律,a较大时散射光强与波长的关系不再明显。用白光照射由大颗粒组成的物质时(如天空的云层等),散射光仍为白色。气体液化时,在临界状态附近由密度涨落引起的不均匀区域的线度比波长要大,所产生的强烈散射使原来透明的物质变混浊,称为临界乳光。
- 相关百科
- 相关知识
- 相关专栏
- 散射辐射测量用遮光球式全自动太阳跟踪器
- 散装水泥管理与技术装备
- 敦化市大福门业有限公司
- 敦煌市海安消防技术咨询有限责任公司
- 敦煌文旅集团有限公司
- 敦煌晶澳光伏电力开发有限公司
- 数位讯号处理器
- 数值孔径计
- 数值计算平台
- 数值计算方法及其程序实现
- 数值计算解题方法与同步训练
- 数值预报方法
- 数字万用表TES2730(RS232)
- 数字人民币硬钱包充电桩
- 数字保存系统
- 数字信号处理:原理、实现及应用——基于MATLAB/Simulink与TMS320C55
- 基于Raman散射线型光纤感温火灾探测器优化设计
- 利用光纤拉曼散射温度传感系统电力电缆温度在线监测
- 基于自发布里渊散射双路分布式光纤传感器设计与实现
- SH波作用下地表覆盖层对浅埋圆孔散射与动应力集中的影响
- 不同土壤类型的粗糙地面与其下方埋藏目标复合电磁散射研究
- SH波对浅埋圆形弹性夹杂附近任意三角形凸起地形的散射
- 分形地面与半埋矩形截面目标复合电磁散射FDTD
- 大功率单频多芯光纤放大器中抑制受激布里渊散射的分析
- 1064nm激光抽运单模光纤受激喇曼散射的理论分析
- 小角X射线散射确定Lc4铝合金时效析出粒子的体积
- 无序电子系统中自旋轨道散射对Hall电导率的影响
- SH波在浅埋可移动圆柱形刚性夹杂处的散射与地震动
- 反向泵浦光纤喇曼放大器中双重瑞利散射噪声的抑制
- 不同表面结构涂层的建筑玻璃后向散射特性的研究
- 柱面SH波在地下圆形衬砌洞室周围散射解析解
- 散射地震波CT技术在某隧道超前地质预报中的应用