随机数发生器应用介绍
生成基于一个给定的范围内的随机数。
产品特点:
-负和实数代人;
-代给定的数整除的数字;
-指定大小的随机数生成列表,独特的标志;
-有用的和有竞争力的用户界面;
-结果格式设置(字体大小,数字格式等等)。
随机数发生器造价信息
理财购物类软件
支持Android 2.1
随机数发生器应用介绍常见问题
-
这样输入 =RANDBETWEEN(-10,10)
-
没有问题,设置雷击发生器的能量输出,符合压敏电阻的承受范围内进行测试。ps,雷击发生器hv对com短路冲击都没有问题的。
-
函数发生器和信号发生器的区别:由于构造不一样,导致产生信号的频率不同,用途就不同。信号发生器(signal generator)解释:是一种能提供各种频率、波形和输出电平电信号的设备,又称信号源或振荡...
随机数发生器应用介绍文献

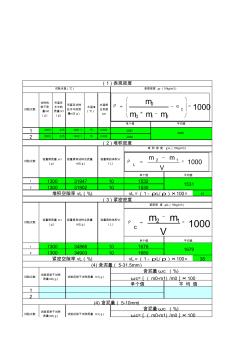 粗骨料记录随机数
粗骨料记录随机数
1 2000 225 1481.1 15 0.002 2 2000 225 1482.1 15 0.002 1 2 43 1 2 38 1 2 容量筒的体积V (L) 1531 2688 容量筒和试样总质量 m2(g) 容量筒的体积V (L) 试验次数 试验次数 试验次数 试验次数 试验次数 试样的 烘干质 量m0 (g) 吊篮在 水中的 质量m1 (g) 试验前烘干试样 质量m0(g) (4) 含泥量( 5-10mm) 含泥量ωc (%) ωc=[(m0-m1) /m0]× 100试验后烘干试样质量 m1(g) (4) 含泥量( 5-31.5mm) 含泥量ωc (%) ωc=[(m0-m1) /m0]× 100 单个值 平 均 值 试验后烘干试样质量 m1(g) 试验前烘干试样 质量m0(g) 1300 34903 10 1680 紧密空隙率 vL(%) vL=(1-ρL/ρ)×100=
这是一个由美国国家标准协会(NIST)制定并被美国国家安全局(NSA)大力提倡的随机数发生器。Dual_EC_DRBG利用椭圆曲线算法的机制生成随机数。这个算法涉及到在曲线上取点并反复在椭圆曲线上进行“打点”操作。该算法公布之后,据报道可能存在一个后门程序,可以根据一个密码完全预测其返回的数字顺序。最近,RSA公司由于其安全产品生产线上的随机数发生器被设置为默认的伪随机数发生器而召回了它的部分产品。无论这种随机数发生器是否被写了后门程序都不会改变椭圆曲线技术本身的力量,但这确实引起了关于对椭圆曲线标准化过程的一些问题。这也是我们应该将注意力用在确保系统充分使用随机数的部分原因。
在NIST SP 800-90A中包含Dual_EC_DRBG的既定目的是其安全性基于数论的计算硬度假设。数学安全性降低证明可以证明,只要理论问题的数量很难,随机数发生器本身就是安全的。但是,Dual_EC_DRBG的制造商没有公布Dual_EC_DRBG的安全性降低,并且在NIST草案发布后不久就发现了Dual_EC_DRBG确实不安全,因为它每轮输出太多比特。太多位的输出(以及精心选择的椭圆曲线点P和Q)是使NSA后门成为可能的原因,因为它使攻击者能够通过强力猜测来恢复截断。在最终发布的标准中没有更正过多位的输出,使得Dual_EC_DRBG既不安全又无后顾之忧。
在许多其他标准中,意味着任意的常数是通过我的套数原则选择的,其中常数是从例如pi中得出的,其方式几乎没有调整的余地。但是,Dual_EC_DRBG没有指定如何选择默认的P和Q常量,可能是因为它们是由NSA构造为后门的。由于标准委员会意识到了后门的可能性,因此包括了实施者选择自己的安全P和Q的方法。但是标准中的确切表述是这样的,即FIPS 140-2验证需要使用所谓的后向P和Q,因此OpenSSL项目选择实施后门P和Q,即使他们意识到潜在的后门并且更愿意生成他们自己的安全P和Q. 纽约时报后来写道,国家安全局在标准化过程中起作用,最终成为该标准的独立的一个编辑。
后来由Daniel RL Brown和KristianGjøsteen为Dual_EC_DRBG发布了安全证明,表明生成的椭圆曲线点与均匀随机椭圆曲线点无法区分,并且如果在最终输出截断中输出的位数较少,如果两个椭圆曲线点P和Q是独立的,如果显示三个问题很难(通常只接受其中一个是硬的),那么Dual_EC_DRBG是安全的。证据依赖于三个问题很难的假设:决策性的Diffie-Hellman假设(通常被认为很难),以及两个通常不被认为难以解决的新问题:截断点问题和x-对数问题。与许多替代CSPRNG(没有安全性降低)相比,Dual_EC_DRBG相当慢,但Daniel R.L.Brown认为安全性降低使得慢速Dual_EC_DRBG成为一种有效的替代方案(假设实现者禁用明显的后门)。请注意,Daniel R.L. Brown为椭圆曲线加密专利的主要所有者Certicom工作,因此在推广EC CSPRNG时可能存在利益冲突。
所谓的NSA后门将允许攻击者通过查看单轮(32字节)的输出来确定随机数生成器的内部状态;然后可以容易地计算随机数发生器的所有未来输出,直到用外部随机源重新接种CSPRNG。这使得例如SSL / TLS易受攻击,因为TLS连接的设置包括以明文形式发送随机生成的加密随机数。NSA所谓的后门将取决于NSA知道e * Q = P的单个e - 这是一个难题,给定Q和P,但如果你可以选择P和Q则容易生成。因此,e是一个秘密密钥,据推测只有NSA才知道,所谓的后门是一个盗版非对称隐藏后门。Matthew Green的博客文章“Dual_EC_DRBG的多重缺陷”通过使用Crypto 1997中引入的离散日志kleptogram,对所谓的NSA后门如何工作进行了简化解释。
取中法
i:平方取中法:
这个方法是由冯·诺伊曼在1946年提出的,思想很简单:
选择一个m位数Ni作为种子,做平方运算(记为Ni+ 1 = (Ni * Ni)...),结果若不足2m个位,在前补0。在这个数选中间m个位的数作为Ni+1。这个算法明显又很大弊端,不仅周期短而且分布不均匀,比如10000平方取中结果就一直为00000了。
ii:常数取中法:
此方法与平方取中法稍有不同,只是把一个随机数的平方换成了随机数与常数的乘积(记为Ni+1 = (K * Ni)...),对于随机分布等没有什么提升。
iii:乘法取中法:
此方法是对平方取中法的一定优化,公式记为Ni+1 = (Ni * Ni-1)...
同余法
同余是啥不知道的同学见我《素性测试》中的wilson检测中有解释
同余法是大部分变成语言的RNG所采用的算法,线性同余方程为:Ni+1 = a Ni + C (mod m),其中a为乘子,C为增量,m为膜。产生的随机序列Rn = Ni / m。
当 a = 1 并且 C != 0时,此同余法称为加法同余法
当a != 1 并且 C = 0时,此同余法称为乘法同余法
当a != 1 并且 C != 0时,此同余法称为混合同余法
同余法当m越大,Ni的范围也就越大,随机分布的也就越均匀,Rn也就分布的更均匀,所以m取值应尽可能的大,充分利用计算机字长。对于如何获得满周期随机数是存在判定定理的,当且仅当满足下列条件时,践行同余法是满周期的:
1.C与m互质
2.对于m的每一个质因子p,(a-1)为p的倍数
3.若m可被4整除, (a-1)也可被4整除。
除此之外还有二次同余,三次同余等,原理差不多。
移位法
由于计算机特有的逻辑移位运算,可以对种子N0左移n位得到M1,右移n位得到M2,将M1与M2做逻辑相加运算得到随机数N1,
公式为Ni+1 = Ni >> n + Ni << n.移位法速度非常快,但对初始值要求较高,很难得到满意的随机序列。
梅森旋转算法
梅森旋转算法是当今生成随机数质量最好的算法,如php,python,perl等流行编程语言内置的PRNG都是采用该算法实现。
下面是来至wiki的介绍:
梅森旋转算法(Mersenne twister)是一个伪随机数生成算法。由松本真和西村拓士在1997年开发,基于有限二进制字段上的矩阵线性地鬼。可以快速产生高质量的伪随机数, 修正了古典随机数发生算法的很多缺陷 。
- 相关百科
- 相关知识
- 相关专栏
- 验电器工频正弦波高压发生器
- 乙酸钌
- MB-K-E系列臭氧发生器
- 羟乙酸异丙酯
- 水处理用臭氧发生器
- HSXZGF-60KV/2mA直流高压发生器
- 受迫对流换热发生器
- 氰基乙酸叔丁酯
- MB-DY系列大型臭氧发生器
- 氧气机发生器
- 数显超声波发生器
- 氯乙酸正丙酯
- 氧化醋酸AS-D萘酚酯酶染色
- GC空气发生器
- 水处理系列臭氧发生器
- 组合燃气式二氧化碳发生器
- 分形DGS单元结构设计及其在微带电路中的应用
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 云计算技术在城市轨道交通运营指挥管理系统中的应用
- 应对水源突发污染的城市供水应急处理技术与应用
- 有限元法在软土浅埋隧道施工过程的动态模拟中的应用
- 新型基于热力学法的水泵效率数学模型及应用
- 振冲碎石桩地基加固技术在椒江标准海塘工程中的应用
- 应用亚温淬火工艺解决45钢槽型螺母淬裂问题的探索
- 乙烯基树脂混凝土电解槽的性能及在湿法冶金中的应用
- 应用清单招标与经评审的最低投标价法评标的几点思考
- 智能化技术在电气工程自动化控制中的应用与实践研讨
- 应用型人才培养模式下高校机电工程综合实践改革探索
- 智能电力监控管理系统在某飞机维修公司工程中的应用
- 异形人工挖孔桩和预应力土层锚杆组合在基坑中的应用
- 智能照明系统在高校教学楼建筑节能改造中的应用
- 圆形截面预应力钢筋混凝土悬臂式支护桩的分析与应用
