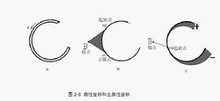
扇性坐标

高斯- 克吕格投影是按分带方法各自进行投影，故各带坐标成独立系统。以中央经线投影为纵轴(x), 赤道投影为横轴(y),两轴交点即为各带的坐标原点。纵坐标以赤道为零起算，赤道以北为正，以南为负。我国位于北半球，纵坐标均为正值。横坐标如以中央经线为零起算，中央经线以东为正，以西为负，横坐标出现负值，使用不便，故规定将坐标纵轴西移500公里当作起始轴，凡是带内的横坐标值均加 500公里。由于高斯-克吕格投影每一个投影带的坐标都是对本带坐标原点的相对值，所以各带的坐标完全相同，为了区别某一坐标系统属于哪一带，在横轴坐标前加上带号，如(4231898m,21655933m)，其中21即为带号。

游戏和图形开发中常用的坐标系有：世界坐标系、物体坐标系、摄像机坐标系、惯性坐标系。 世界坐标系是描述其它坐标系所需要的参考框架，只能用世界坐标系描述其他坐标系的位置，不能用更大的，外部的坐标系来描述世界坐标系。

关于世界坐标系的的典型问题都是关于初始位置和环境的，如：

1、 每个物体的位置和方向。 2、摄像机的位置和方向。 3、世界的每一点的地形是什么。 4。各物体从哪里来，到哪里去。 物体坐标系是和特定物体相关的坐标系。每个物体都有它们独立的坐标系。 在物体坐标系中可能会遇到的问题： 1、周围有需要互相作用的物体吗？（我要攻击它吗？） 2、哪个方向，在我前面吗？我左边一点？（我应该射击还是转身就跑） 摄像机坐标系是和观察者密切相关的坐标系。是一种特殊的“物体”坐标系。 典型问题： 1、3D空间中的给定点在摄像机前方吗？ 2、3D空间中的给定点在屏幕上还是超出了边界？ 3、某个物体是否在屏幕上？部分还是全部在？ 4、两个物体谁在前面？（可见性检测，深度排序） 惯性坐标系是为了简化世界坐标系到物体坐标系的转换。从物体坐标系到惯性坐标系只需旋转，从惯性坐标系到世界坐标系只需平移。 嵌套坐标系同样为了简化物体在世界坐标系中位置，如一个物体坐标系嵌套一个头部坐标系，则头部坐标系可以只与物体坐标系联系，简化操作。

坐标系转换，应用矩阵表示，一切操作如物体的旋转、平移过程等都可以用矩阵(4*4齐次空间矩阵)来表示2100433B

相对坐标系笛卡尔坐标系

定义 ：笛卡尔坐标系 就是直角坐标系和斜角坐标系的统称。 相交于原点的两条数轴，构成了平面放射坐标系。如两条数轴上的度量单位相等，则称此放射坐标系为笛卡尔坐标系。两条数轴互相垂直的笛卡尔坐标系，称为笛卡尔直角坐标系，否则称为笛卡尔斜角坐标系。 笛卡尔坐标，它表示了点在空间中的位置，但却和直角坐标有区别，两种坐标可以相互转换。

介绍

笛卡尔坐标系 (Cartesian coordinates) 就是直角坐标系和斜角坐标系的统称。

相交于原点的两条数轴，构成了平面放射坐标系。如两条数轴上的度量单位相等，则称此放射坐标系为笛卡尔坐标系。两条数轴互相垂直的笛卡尔坐标系，称为笛卡尔直角坐标系，否则称为笛卡尔斜角坐标系。

推广

放射坐标系和笛卡尔坐标系平面向空间的推广

相交于原点的三条不共面的数轴构成空间的放射坐标系。三条数轴上度量单位相等的放射坐标系被称为空间笛卡尔坐标系。三条数轴互相垂直的笛卡尔坐标系被称为空间笛卡尔直角坐标系，否则被称为空间笛卡尔斜角坐标系。

笛卡尔坐标，它表示了点在空间中的位置，但却和直角坐标有区别，两种坐标可以相互转换。举个例子：某个点的笛卡尔坐标是493 ,454, 967，那它的X轴坐标就是4 9 3=16，Y轴坐标是4 5 4=13，Z轴坐标是9 6 7=22，因此这个点的直角坐标是(16, 13, 22)，坐标值不可能为负数（因为三个自然数相加无法成为负数）。

相对坐标系球坐标系

球坐标是一种三维坐标。分别有原点、方位角、仰角、距离构成。

设P（x，y，z）为空间内一点，则点P也可用这样三个有次序的数r，φ，θ来确定，其中r为原点O与点P间的距离，θ为有向线段与z轴正向所夹的角，φ为从正z轴来看自x轴按逆时针方向转到有向线段在坐标平面xoy的投影所转过的角，这里M为点P在xOy面上的投影。这样的三个数r，φ，θ叫做点P的球面坐标，这里r，φ，θ的变化范围为

r∈[0, ∞),

φ∈[0, 2π],

θ∈[0, π] .

当r,θ或φ分别为常数时,可以表示如下特殊曲面:

r = 常数，即以原点为心的球面；

θ= 常数，即以原点为顶点、z轴为轴的圆锥面；

φ= 常数，即过z轴的半平面。

与直角坐标系的转换:

1).球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:

x=rsinθcosφ

y=rsinθsinφ

z=rcosθ

2).反之,直角坐标系(x,y,z)与球坐标系(r,θ,φ)的转换关系为:

r= sqrt(x*2 y*2 z*2);

φ= arctan(y/x);

θ= arccos(z/r);

球坐标系下的微分关系:

在球坐标系中，沿基矢方向的三个线段元为：

dl(r)=dr, dl(θ)=rdθ, dl(φ)=rsinθdφ

球坐标的面元面积是：

dS=dl(θ)* dl(φ)=r^2*sinθdθdφ

体积元的体积为：

dV=dl(r)*dl(θ)*dl(φ)=r^2*sinθdrdθdφ

球坐标系在地理学、天文学中有着广泛应用.在测量实践中，球坐标中的θ角称为被测点P（r，θ，φ）的方位角，90°－θ成为高低角

相对坐标系世界坐标系

世界坐标系" 在学术文献中的解释

1、世界坐标系定义为:带有小圆的圆心为原点ow,xw轴水平向右,yw轴向下,zw由右手法则确定.,v′n为实时图中对应的统计特征向量

2、是系统的绝对坐标系也称为世界坐标系.在没有建立用户坐标系之前画面上所有点的坐标都是以该坐标系的原点来确定各自的位置的

3、设一个基准坐标系Xw—Yw—Zw称为世界坐标系,(xw,yw,zw)为空间点P在世界坐标系下的坐标.(u,v)为P点在图像直角坐标系下的坐标

4、这个坐标系称为世界坐标系.计算机对数量化

在AutoCAD中：

世界坐标系 用于图形转换的起始坐标空间。最大尺寸是 2^32单位高和 2^32 单位宽。

支持缩放、平移、旋转、变形、投射等转换操作。

世界坐标系统(WCS)是AutoCAD的基本坐标系。

绘图期间，原点和坐标轴保持不变。世界坐标系由三个互相垂直并相交的坐标轴X,Y,Z组成。

默认情况下，X轴正向为屏幕水平向右，Y轴正向为垂直向上，Z轴正向为垂直屏幕平面指向使用者。坐标原点在屏幕左下角。

相对坐标系三维坐标系

三维笛卡儿坐标系是在二维笛卡儿坐标系的基础上根据右手定则增加第三维坐标（即Z轴）而形成的。同二维坐标系一样，AutoCAD中的三维坐标系有世界坐标系WCS(World Coordinate System)和用户坐标系UCS(User Coordinate System)两种形式。

右手定则：

在三维坐标系中，Z轴的正轴方向是根据右手定则确定的。右手定则也决定三维空间中任一坐标轴的正旋转方向。

要标注X、Y和Z轴的正轴方向，就将右手背对着屏幕放置，拇指即指向X轴的正方向。伸出食指和中指，食指指向Y轴的正方向，中指所指示的方向即是Z轴的正方向。

要确定轴的正旋转方向，用右手的大拇指指向轴的正方向，弯曲手指。那么手指所指示的方向即是轴的正旋转方向。

用户坐标系（UCS）

用户坐标系：

为坐标输入、操作平面和观察提供一种可变动的坐标系。定义一个用户坐标系即改变原点（0，0，0）的位置以及XY平面和Z轴的方向。可在AutoCAD的三维空间中任何位置定位和定向UCS，也可随时定义、保存和复用多个用户坐标系。2100433B