三代角定理
三代角定理用来计算在一个母角角度在360以内的角均分成N份(N可以非整数)后,得到N个子角,然后在该母角以及每个子角上做弦,其各个(子角的弦或者弦延长线)与(母角的弦或者延长线)自然相交的角度,这里称这种角为孙角。
三代角定理基本信息
| 中文名称 | 三代角定理 | 公式 | z*(n/2+0.5-t)=m*(n/2+0.5-t)/n |
|---|---|---|---|
| z | 子角的度数 | n | 把母角分成多少等份 |
三代角定理造价信息
三代角定理常见问题
-
【= =,楼上的,他已经说了只能用勾股定理,用正弦定理和余弦定理楼主看不懂啊】 使用勾股定理,在于对特殊角60°,45°的使用 解:1)作BF⊥DA延长线于F ∵CD⊥DF ∴∠FDC=90° ∵∠B...
-
没有圆切角定理,只有弦切角定理:弦切角等于它所夹的弧对的圆周角
-
首先更正一下,是弦切角,老沈瞎说呢。你把图画出来,AB是圆O切线,AC是弦。做过切点A的直径,交圆O于A、D。连接B、D。证明:因为AD是圆O直径,AB是圆O切线所以∠C=90°=∠BAD所以∠BAC...
三代角定理文献

 第三代碳纤维技术
第三代碳纤维技术
相比传统的金属材料和其他纤维制成的复合材料, 碳纤维复合材料具备质量 轻、强度高、弹性模量高的特点,可比传统铝合金结构减重 30%,对武器装备性 能提升贡献巨大,被广泛用于制造航空器机体及发动机、 导弹外壳等。美国 F-22、 F-35 战斗机的碳纤维复合材料用量比例分别达到 24%和 36%,以 A350、波音 787 为代表的新型大型民机的碳纤维复合材料用量比例更是达到了 50%以上。 碳纤维复合材料的运用已成为衡量武器装备先进性的标志之一。 碳纤维是构 成复合材料的关键原材料,承担着复合材料约 90%的载荷,其拉伸强度和弹性模 量是实现复合材料结构性能目标的关键。 碳纤维复合材料生产和应用技术已经是 航空工业制造水平的重要标志之一。 市场发展 高端碳纤维市场一直为日美两国所垄断。 高端碳纤维绝大部分是小丝束的聚 丙烯腈( PAN)基碳纤维。 目前全球最主要的 6家小丝束碳纤维供应商的

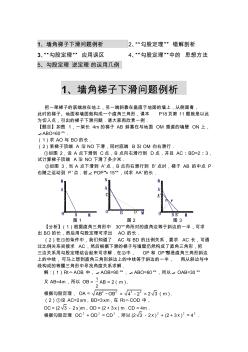 墙角梯子下滑问题及勾股定理
墙角梯子下滑问题及勾股定理
1、墙角梯子下滑问题例析 2、“勾股定理” 错解剖析 3、“勾股定理” 应用误区 4、“勾股定理”中的 思想方法 5、勾股定理 逆定理 的运用几例 1、墙角梯子下滑问题例析 把一架梯子的底端放在地上,另一端斜靠在垂直于地面的墙上,从侧面看, 此时的梯子、地面和墙面就构成一个直角三角形,课本 P18页第 11题就是以此 为切入点,引出的梯子下滑问题.请大家再欣赏一例. 【题目】如图 1,一架长 4m的梯子 AB 斜靠在与地面 OM 垂直的墙壁 ON 上, ∠ABO=60°. (1)求 AO 与 BO的长. (2)若梯子顶端 A 沿 NO 下滑,同时底端 B 沿 OM 向右滑行. ①如图 2,设 A 点下滑到 C点,B 点向右滑行到 D点,并且 AC∶BD=2∶3, 试计算梯子顶端 A 沿 NO 下滑了多少米. ②如图 3,当 A 点下滑到 'A 点,B点向右滑行到 'B 点时,梯子 AB 的
从一个角的顶点引出的把这个角分成两个相等的角的射线,叫做这个角的角平分线。
三角形的一个角(内角)的角平分线交其对边的点所连成的线段,叫做这个三角形的一条角平分线。
角平分线定理定理1
角平分线上的点到这个角两边的距离相等。
证明:如图1,AD平分∠BAC,DB⊥AB,DC⊥AC
∵AD是∠BAC的平分线
∴∠BAD=∠CAD
∵DB⊥AB,DC⊥AC,垂足分别为B、C
∴∠ABD=∠ACD=90°
又 AD=AD
∴△ABD≌△ACD
∴CD=BD
故原命题得证。
该命题有逆定理:
逆定理:在角的内部到一个角的两边距离相等的点在这个角的角平分线上。
证明:如图,DB⊥AB,DC⊥AC,且DB=DC
∵DB⊥AB,
∴∠DBA=90
同理∴∠DCA=90
在RT△DBA和RT△DCA中,
{DB=DC(已知)
AD=AD(公共边)
∴RT△DBA≌RT△DCA(HL)
∴∠BAD=∠CAD(全等三角形对应角相等)
角平分线定理定理2
三角形一个角的平分线与其对边所成的两条线段与这个角的两边对应成比例。
证明:如图2,在△ABC中,AD是∠BAC的平分线
过点D作DE⊥AB,DF⊥AC
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC
∴DE=DF(定理1)
∵2S△ABD=AB×DE,2S△ACD=AC×DF
∴S△ABD:S△ACD=AB:AC
过点A作AG⊥BC,垂足为G
∵2S△ABD=BD×AG,2S△ACD=CD×AG
∴S△ABD:S△ACD=BD:CD
∴AB:AC=BD:CD
故原命题得证。
该命题有逆定理:
如果三角形一边上的某个点与这条边所成的两条线段与这条边的对角的两边对应成比例,那么该点与对角顶点的连线是三角形的一条角平分线。
证明略。
角平分线定理角平分线长
由定理2和斯特瓦尔特定理可以推导出三角形内的角平分线长公式。
如右图3,在△ABC中,AD平分∠BAC
可设AB=x,AC=y,BD=u,CD=v,则BC=u v
由定理2我们知道 AB:AC=BD:CD,所以xv=uy
由斯台沃特定理,有w²=(x²v y²u)/(u v)-uv
用u=xv/y,v=uy/x替换原式中的u和v
即得AD²=xy-uv=AB×AC-BD×DC
如图2,若AB,AO分别是平面a的垂线和斜线,OB是AO在平面a内的射影,∠AOB为锐角,OC是平面a内和OB不重合的任一直线,在OC上截取OD=OB,连结AD,则AB
在△AOB与△AOD中,因为OA=OA,OB=OD,AB
定理得证。
上述定理是定义“斜线和平面所成的角”这一概念的理论基础。有了上面的性质,就保证了这一概念的定义的合理性 。
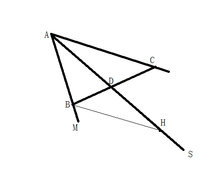
角平分线性质定理逆定理
【角平分线逆定理】
1.到角两边的距离相等的点在角平分线上。
2.平面内任意一小于180度的∠MAN如图,直线BC分别交半直线AM、AN、AS于B、C、D,AB/BD=AC/CD则:AS平分∠MAN
下面给出证明过程:
证明:过B作BH∥AC交AS于H
∴△ADC∽△HDB(∠ADC=∠HDB,∠ACD=∠HBD)
∴AC/CD=HB/BD
又AB/BD=AC/CD
∴AB=BH
∴∠BHA=∠BAH=∠HAC
∴AS平分∠MAN
- 相关百科
- 相关知识
- 相关专栏
- 通州新城
- 电机扩大机
- 彩色扩印机
- 脉冲功率科学与技术
- 机电伺服系统
- 流纹岩矿床
- 高级维修电工技术与实例
- FED5
- 投影晒印
- 照相分色
- 定位轴线
- 新加坡地铁滨海市区线
- 遥感图像处理输出设备
- 优越者Y-C137
- 康桥原溪里
- enlarger
- 简易六角砖铺设装置CN109537417A
- 永州市冷水滩区岚角山街道本级农村综合服务平台工程
- 影响度视角的项目前期策划阶段造价影响因素分析
- 关于固定式太阳能路灯照明系统电池组件最佳安装角度
- 工程项目全过程跟踪审计控制探析基于建设方视角
- 关于电网工程总承包项目施工角色定位及标准化管理
- 广东珠江三角洲环境项目某污水处理部分咨询服务合同
- 恒智天成安全计算软件三角形钢管悬挑脚手架计算书汇总
- 工程图样中六角螺母在AutoCAD中近似画法改进
- 基于PLC控制星三角启动存在问题及解决办法
- 构建对内联接通道发挥北承长江三角洲桥头堡作用
- 化油器三角针阀与阀座导致油耗高与溢油问题解决办法
- 基于PSD光电自准直仪测量空间两平板相对倾角变形
- 互惠性偏好视角下PPP项目社会资本控制权分配模型
- 国内外钢结构设计规范关于角焊缝限值及计算方法比较
- 建筑无足够附着角度塔吊超长距离附着解决方案
