绕流阻力压差阻力
由于边界层分离,物面压强发生很大变化,特别是物体尾部形成尾流区,压强降低,形成上下游较大压强差。压强沿物面积分可得压差阻力,亦称形状阻力 。
绕流阻力造价信息
绕流阻力是指绕流物体表面的流体所受摩擦阻力和压差阻力的总和。表面摩擦阻力即物体表面切应力的积分,可由遗界层理论计算 。
压差阻力一般需通过试验确定。如果将分离点推向下游,减小尾流区,则压差阻力将随之降低。一般说来,当水流雷诺数Re较高时,表面摩阻力将比压差阻力小很多。因此,要降低绕流阻力,首先要设法降低压差阻力,例如使绕流物体流线型化 。
绕流阻力压差阻力常见问题
-
应该是800倍。“贴着水面射击弹头可能会瞬间破裂”,也是不成立的。因为像木头、泥土(包括本题的冰)一类的物质相对于空气的阻力要远远大于水的800倍,也未见其弹头破裂,可以肯定,金属的弹头无论何种情况下...
-
你好,在供热系统设计时,尽量减少串联设计,特别减少钢制搭接焊暖气片、钢制板型暖气片等大阻力暖气片的直接串联;做好横水管的连接口,尽量让其与系统管道配套,减少因管道突然缩小而带来的损失;做好暖气片散热量...
-
1.品牌: POWERCHAN,安装方式: 内藏式/无盖式,材质: 锌合金,厚度: 2mm,底座: &n...
绕流阻力系数的表达式为:
式中,D为阻力;P为流体密度;U∞为来流速;A为物体迎流面积。物体形状、壁面粗糙情况、来流紊动强度、水流雷诺数都是影响Cp的因素 。
如图《二维物体绕流阻力系数》和《三维物体绕流阻力系数与雷诺数的关系曲线》所示:
2100433B
绕流阻力压差阻力文献

 矩形通道内脉动层流阻力特性实验研究
矩形通道内脉动层流阻力特性实验研究
针对简谐脉动层流条件下矩形通道内的阻力特性进行理论和实验研究。基于脉动条件下矩形通道内层流流动的数学模型,分析了脉动周期、脉动振幅等因素对摩阻常数的影响,并进行实验验证。结果表明:脉动层流摩阻常数与脉动周期、脉动振幅、通道高宽比和流体性质有关;层流摩阻常数理论值与实验值相吻合,脉动周期越小或相对振幅越大,层流摩阻常数的峰值越大、谷值越小,层流摩阻常数脉动的幅度越大。

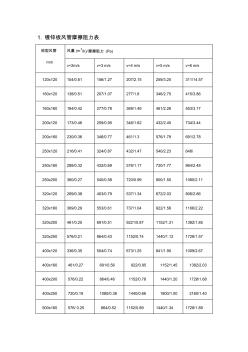 风管沿程阻力、散流器阻力
风管沿程阻力、散流器阻力
1. 镀锌板风管摩擦阻力表 矩型风管 mm 风量 (m3/h)/摩擦阻力 (Pa) v=2m/s v=3 m/s v=4 m/s v=5 m/s v=6 m/s 120x120 104/0.61 156/1.27 207/2.15 259/3.25 311/14.57 160x120 138/0.51 207/1.07 277/1.8 346/2.75 415/3.86 160x160 184/0.42 277/0.78 369/1.49 461/2.26 553/3.17 200x120 173/0.46 259/0.95 346/1.62 432/2.45 734/3.44 200x160 230/0.36 346/0.77 461/1.3 576/1.79 691/2.78 250x120 216/0.41 324/0.87 432/1.47 540/2.23 648
前言
主要符号说明
第1章 绪论
1.1 研究背景
1.2 研究方法评述
1.3 研究现状及发展趋势
1.4 主要成果
1.5 本书主要研究问题
参考文献
第2章 桩基绕流理论分析研究
2.1 势流理论简述
2.2 边界层理论简述
2.3 涡旋理论简介
2.4 实际水流绕流圆柱机理研究
2.5 本章小结
参考文献
第3章 桩基绕流数值模拟
3.1 桩基绕流数值模拟研究的意义
3.2 流体动力学控制方程
3.3 控制方程离散方法的选择
3.4 模拟方法的选择
3.5 平面二维桩柱绕流数值模拟
3.6 波流作用下桩基绕流的数值模拟
3.7 本章小结
参考文献
第4章 桩基绕流物理测试研究
4.1 桩柱绕流阻力测试研究
4.2 桩群绕流阻力测试研究
4.3 桩群绕流对水流影响测试研究
4.4 桩群局部冲淤特性测试研究
4.5 本章小结
参考文献
第5章 结论与展望
5.1 主要成果与结论
5.2 展望2100433B
沿程阻力——流动中水流内摩擦力(黏性力)。
局部阻力——局部边界突变引起流速突变产生的惯性力(如断面突大突小或闸阀等) 。
流体流动阻力:流体在管路系统中的流动可以分为在均匀直管中的流动,产生以表面摩擦为主的沿程阻力;在各种管件象阀门、弯管、设备进出口等中的流 动,由于流道变向、截面积变化、流道分叉汇合等 产生以逆压差或涡流为主的局部阻力。
流动边界的物体对流动流体的作用力。它与流体流动的方向相反,由动量传递而产生。流动阻力是粘性流体中动量传递研究的基本问题之一。流动阻力的反作用力,即流体对物体的作用力,称为曳力(drag)。对于管流,流动阻力通常用流体的压力降表示,此压力降造成的机械能(压能)降低不能再恢复,亦即部分机械能遭受损失,通称阻力损失。对于绕流,更多地注意曳力。只要来流即物体上游流体速度均匀,流体绕过静止物体的流动,与物体在静止流体中的运动是等同的。因此,工程上常在流动流体中置入静止的模型,以模拟物体在静止流体中的运动。
1506年,意大利科学家达·芬奇首先提出物体在流体中运动会受到阻力的观点,此后I.牛顿等著名科学家都曾作有关研究,然而直到边界层理论产生之后,才认识到流动阻力的实质。产生阻力的原因,早期只考虑物体前部的形状,后来发现物体后部的形状才是量重要的。物体后部发生的边界层分离,对流动阻力起决定性的影响。
种类 分为摩擦阻力和压差阻力。摩擦阻力是物体表面剪切力产生的流动阻力,其方向与流体运动方向相反。压差阻力则是垂直于物体表面的压力产生的对流体流动的阻力,其方向也与流体运动方向相反。两种阻力常同时存在。以流体绕过某物体的流动为例,两种阻力的相对大小取决于下列三个因素:①物体的形状,如果物体是球那样的钝体,边界层分离较早,压差阻力是主要的。对于流线型物体,边界层不分离或分离较迟,则压差阻力较小,摩擦阻力是主要的。②由物体特征长度决定的雷诺数的大小,雷诺数决定边界层中的流动状态。湍流边界层摩擦阻力较大,但因分离推迟,往往压差阻力较小;层流则相反,摩擦阻力较小,而压差阻力较大。③物体表面的粗糙度,粗糙表面的摩擦阻力较大,但粗糙表面可促进边界层湍化,使分离推迟,从而减小压差阻力。
阻力计算 绕流时阻力F的计算式为:式中Cd为阻力系数;u为来流速度;A为物体在垂直于运动方向上的投影面积;ρ为流体密度。阻力系数Cd的大小取决于物体形状和雷诺数。如液体绕流圆球时的阻力系数Cd与Re的关系曲线(见绕流)。
流体在管道中流动时,直管的阻力主要是摩擦阻力,又称沿程阻力。摩擦阻力表示为壁面上的剪切应力τw,其计算式为:式中f称为范宁摩擦系数;u为流体平均速度。τw与管内压力降 Δp成正比,所以管内摩擦阻力常以压力降表示,计算式为:式中l为管长;d为管道直径;λ是摩擦系数(λ=4f),它是Re数和粗糙度ε(管壁上突出物的平均高度)的函数,即:
λ=φ(Re,ε/d)
上述函数关系可由实验或理论计算得到(见管流)。管内流体流经各种局部障碍物(例如阀门和管内构件),或通道截面积突然扩大或缩小时所产生的阻力主要是压差阻力,工程上称为局部阻力。这时虽然也有摩擦阻力存在,但一般很小,可以忽略。对于管流局部阻力的计算常用下式:式中ξ为局部阻力系数,其值由实验确定。
研究流动阻力的意义 在工程应用上,研究流动阻力的目的是:①计算能量消耗,确定所需加入流动系统的外功,以便选择流体输送机械。②寻求减小阻力的方法,以减少能耗。例如:为降低弯曲通道中的阻力,可设置导流叶片;为减小压差阻力,可使物体具有圆头尖尾的细长外形(流线型);为减小通道截面变化时的局部阻力,可采用截面逐渐变化的通道;为降低减压精馏塔的塔板压力降,可采用渐缩通道小孔的文丘里塔板。③通过改变流动阻力进行流量的调节和分配或改善流动截面上的流速分布,即流体均布。例如:在流化床反应器中采用高压力降分布板,迫使流体沿流动截面均匀分布,以消除因床层波动而引起的流体分布不均现象。
- 相关百科
- 相关知识
- 相关专栏
- 绕组线包装第21部分:圆柱形交货线盘基本尺寸
- 绕组线包装第31部分:圆锥形交货线盘基本尺寸
- 绕组绝缘
- 绘制平面等值线图与图框系列
- 绘图仪尺绘图模板
- 绘景景观规划工程(江苏)有限公司
- 绘等值线图法
- 绘设计:城市规划快题设计完全解析
- 给付对价
- 给孩子的世界建筑史
- 给孩子的中外建筑史艺术百科
- 给排水、采暖、燃气工程工程量清单计价应用手册
- 给排水及其设备安装工程基础理论与监理实务
- 给排水工程技术专业课程改革系列教材·道路与桥梁工程施工
- 给排水科学与工程专业大学生创新创业训练与实例
- 给排水科学与工程专业实习指导
- 在“建筑节能与居住舒适”专题技术交流会议上的讲话
- 引江济淮工程淠河总干渠以北安徽段截污导流工程设计
- 基于超磁致伸缩效应的新型液压高速开关阀
- 争创一流大学-同济大学副校长建筑学家李国强访谈录
- 高效率PWM/PFM自动切换升压转换器的设计
- 杂散电容对交流法微电容测量电路噪声特性影响的分析
- 制度流程管理规定发布、作废、制定、审核、批准
- 影响免蒸养(压)粉煤灰小型空心砌块强度指标的因素
- 整流变压器技术规格书(2016.7.5定稿)资料
- 在水泥企业节能环保适用技术交流会上的讲话(摘要)
- 中国农业机械流通协会第三次会员代表大会
- 新型的避免调节阀发生气蚀的方法孔板节流法
- 制造流程中卧式离心水泵与立式离心水泵应该怎么挑选
- 止回阀是指依靠介质本身流动而自动开闭阀瓣用来防止
- 以管道形状的改变来提高风机系统流量的节能方法
- 永磁直流电动机—水泵系统由光伏电池供电的运行分析