桥梁安装容许误差
桥梁安装容许误差基本信息
| 中文名 | 桥梁安装容许误差 | 外文名 | bridge erection tolerance |
|---|---|---|---|
| 所属学科 | 公路交通科学技术 | 公布时间 | 1996年 |
《公路交通科技名词》第一版。 2100433B
桥梁安装容许误差造价信息
1996年,经全国科学技术名词审定委员会审定发布。
桥梁安装容许误差常见问题
-
T字桥梁安装,道理先第一片吊装就位完毕后,在两侧采用钢管支撑固定,第二片桥梁安装完毕后,写上将两片梁用钢筋焊接上,以防空心板梁倾倒及移位。希望你更正。
-
一、梁体吊装前的准备工作 当构件及墩台达到设计强度100%时,经监理及现场技术人员检查合格后方可进行运输安装,安装前要求检查构件的外形尺寸,预埋件尺寸和位置,符合要求的构件方可使用;需要做的准备工作有...
-
这个误差是不可以调整的,只是计算的工程量,你要仔细对比查看,看看工程量的误差到底在什么地方才是,看看预留量是不是都一样等等。
桥梁安装容许误差文献

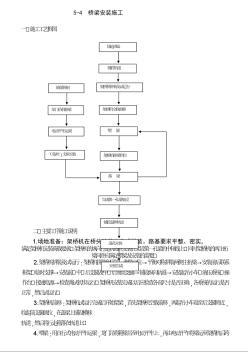 桥梁安装施工
桥梁安装施工
5-4 桥梁安装施工 一、施工工艺框图 场地准备 铺设轨道 安装完成 架桥机拼装及试运行 逐孔安装 铺设延伸轨道 完成第一孔梁架设 落 梁 架桥机移梁到位 架桥机空载前移 喂 梁 (临时)支座安装 箱梁预制 龙门吊机移梁 电动平车运梁 二、主要工序施工说明 1.场地准备:架桥机在桥头路基上完成拼装。路基要求平整、密实, 满足架桥机安装荷载要求。架桥机的纵向行走轨道应安装在架设第一孔梁的中轴线上。同时架桥机的两主桁梁间距应满足喂梁及安装的需要。 2.架桥机拼装及试运行:架桥机拼装程序为:测量定位→平衡对称拼装两侧主桁梁→安装前后联系框架、临时支撑→安装前、中、后支腿及中、后顶高支腿→铺设纵向轨道→安装起吊小车、液压系统、操作台、接通电源→检查调试初步

 桥梁安装施工作业指导书
桥梁安装施工作业指导书
筑 龙 网 WW W. ZH UL ON G. CO M 桥梁安装施工作业指导书 一、适用范围 本作业指导书适用范围:桥梁板安装。 本标段桥梁上部构造有 10m、16m空心板,20m、25m、30m、40m 预制箱梁,根据场地条件拟采用 30-50t吊车配合架桥机进行安装, 其安装工艺如下: 1、安装准备工作 (1)测量放样 安装大梁前,须在墩、台帽上放出每片梁及支座、临时支座的详 细位置,并划线以使大梁准确就位。 检查支座和临时支座位置的标高, 以便在梁板时调整标高。 (2)道路准备 将桥头及运梁车所经便道等安排专人负责整修,保证道路畅通。 (3)人员、设备 人员、设备按时到场,并对运梁、架梁的设备进行详细检修,以 保证在施工过程中不因设备原因影响到施工过程。 (4)临时支座安装 临时支座采用硫磺砂浆浇筑, 其具体尺寸应根据实际情况计算确 定。 ① 硫磺砂浆
容许误差一般流程
为了方便判断,对于医学领域类的抽样调查在确定合适的容许误差时可以采用图1框图所示方法进行初步判断。
容许误差案例分析
容许误差 δ 是假设检验试图揭示的差异大小,δ越小,所需样本含量越大。在假设检验样本含量的估计中,研究者无法得到总体参数间的差值时,可以有三种确定的做法。
若研究者无法得到总体参数间的差值δ,可以通过如下方法获得:1、通过预实验的组间差距作为容许误差δ。2、根据专业知识由各专业的专家确定有专业意义的差值作为容许误差δ,如平均舒张期血压的差值>0.69kPa,白细胞的平均差值0.5×109/L等。3、对于没有给定专业意义上的容许误差水平的情况下,用0.25倍或0.50倍的标准差来设定容许误差 。
容许误差的大小,通常取决于以下几方面的要求和条件:
容许误差精确度要求
对调查结果的精确度要求高,容许误差就应当小,对调查精确度的要求不那么高,容许误差就可以大一些。
容许误差调查预算
包括可以用于调查为人力、物力和财力。调查的人力强,经费充足,容许误差就可以小一些,反之调查的人力较弱,经费不那么充裕,容许误差就可以大一些。
容许误差调查性质
对国民经济、人民生命、健康和政策、决策有很大影响均指标、项目,容许误差就必须小一些,而一般性的质量指标、项目,容许误差就可以大一些。在多目的、多标识调查中,主要项目的容许误差应当小一些,而非主要项目的容许误差则。
我们的抽样调查结果,它的实际误差究竟有多大的可能性会落在我们计算的平均误差范围内呢?这就要应用概率论和大数定律才能回答。
大数定律的正态分布定理表明,大量随机现象的分布,总是遵从正态分布,即多数单位都是围绕在它的平均数两侧这样一种分布状态的。正态分布是概率论中的一种最常见的和最重要的分布,随机事件就是这样的分布规律,不是随机现象就不可能呈正态分布。
根据大数定律的正态分布定理,抽样误差范围的大小和概率的关系是:
| 1 |
68.27% |
| 2 |
95.45% |
| 3 |
99.73% |
| 4 |
99.994% |
| 5 |
99.9999% |
这就是说,如果进行10次抽样调查,有68.27次的抽样误差将不超过正负一个误差即1个μ的范围,其余31.73次将超出这个范围,有95.45次的抽样误差将不超过正负二个误差即2个μ的范围,其余4.5次将超过这个范围,有99.73次将不超过正负三个误差即3个μ的范围,其余0.27次将超过这个范围;依此类推。
但是,通常只作一次抽样调查,对这一次调查来说,在正负一个误差范围内的把握程度就应是66.27%;在正负二个误差范围内的把握程度就应当是95.45%;在正负三个误差范围内99.73%;依此类推。如果还要提高把握程度,还可以扩大到正负四个或五个误差范围。但是这样,把握程度虽然提高了,误差范围也就扩大了。因此,通常搞抽祥调查,一般都只要正负二到三个μ误差范围就行了,因为这样把握程度已经可以达到95.45~99.73%。也就是说,在正负二个μ误差范围内,把握程度已经达到95%以上,在正负三个μ误差范围内,把握程度已经达到99.73%以上,即此时的置信度很高。
调查结果落在一定平均误差范围的概率,就叫把握程度;而一定的平均误差范围就叫做容许误差或可能误差。在一些统计教科书上,也有将把握程度叫做置信程度,而将在一定把握程度下的容许误差或可能误差范围叫做置信区间的。
设用△表示容许误差,t表示误差范围:
- 相关百科
- 相关知识
- 相关专栏
- 桥梁安装监测
- 桥梁实验车
- 桥梁审美原理
- 桥梁容许应力设计
- 桥梁工程上册
- 桥梁工程与施工技术
- 桥梁工程与施工技术研究
- 桥梁工程专业承包企业资质等级标准
- 桥梁工程全寿命设计方法及工程实践
- 桥梁工程地质勘察
- 桥梁工程安全控制教育部重点实验室
- 桥梁工程实用测量
- 桥梁工程师
- 桥梁工程技术习题指导
- 桥梁工程技术经济
- 《桥梁工程技术》
- 中高职衔接道路桥梁工程技术专业教学标准探索与实践
- 增设钢牛腿在连续独柱墩桥梁抗倾覆加固设计中的应用
- 张峰水库2号倒虹预应力钢筒混凝土管道安装施工工艺
- 智能建筑电气安装中的质量控制
- 影响我国公路桥梁板式橡胶支座质量的因素及应对措施
- 引进10000m^3/h空分设备的流程及安装特点
- 中国制冷空调设备维修安装企业资质等级认证评审公示
- 医院工程电气、弱电、消防火灾报警安装工程监理细则
- 智能建筑综合布线系统安装分项检验批质量验收记录表
- 应急柴油发电机组安装00D272机组冷却方式
- 支架、吊架安装检验批模板
- 云南省造价工程师安装计量:除锈、刷油和衬里考试题
- 义龙丽景都市公寓门窗玻璃安装分项工程监理实施细则
- 中分带回填土、路缘石安装及培土路肩施工方案修改后
- 有限公司电力液压电梯门系统安装工程质量验收记录表
- 以位移为基础的钢筋混凝土桥梁墩柱抗震设计方法