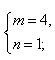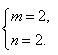平面镶嵌教学流程

教学课堂教学的流程可以大致如下:

课前师生收集镶嵌图案--课堂展示交流有关镶嵌图案--明晰概念(镶嵌)--对所展示图片观察的基础上提出一些有待研究的问题--对学生所提出问题进行适当的归类并进一步引导以展开后续的课堂教学。

学生所提出的问题必将是十分丰富的，同时也可能是十分繁杂的。因此，教师课前应认真分析有关问题，根据学生的学习经验、思维水平以及问题之间的逻辑关系对后续问题的研究进行一个整体的规划，这样才能及时对学生所提出的问题有一个比较好的评判(如对这个问题的研究价值、研究方法、研究难度等作出比较恰当的评判，从而确定这样的问题是否可以在课堂上进行研究，按照什么顺序进行研究等)，从而保证课堂教学的有序而高效地进行。固然，教学中可以有多样的选择，下面仅提出一些建议供参考。

总体而言，教学中应认真分析问题的繁简和难易程度，一般遵循先易后难、先简后繁的顺序展开教学活动。因此，建议首先研究较为简单的单个多边形的镶嵌问题，再研究复杂的多个多边形的组合镶嵌问题。

对于单个多边形的镶嵌问题，基于学生的水平和课程标准的要求，这里主要研究三角形、四边形、正六边形的镶嵌问题。

对于三角形、正六边形以及一些特殊的四边形(如正方形、长方形、平行四边形)的镶嵌问题，学生应该都比较熟悉，因此，教学中，教师可以根据课堂教学状况灵活选择不同的教学顺序。如可以在收集、观察的基础上发现正方形、正六边形等平面图形都可以镶嵌整个平面，然后思考还有哪些正多边形也可以镶嵌整个平面，再从特殊到一般进一步研究一般的多边形(三角形、四边形)的镶嵌问题;也可以在明晰了镶嵌概念之后，直接要求学生想象哪些多边形能够镶嵌平面，并进行具体的纸上描画或者进行实际的拼接(当然，这里就未必有一个确定的教学顺序了，根据课堂学生的状况可能有不同的教学顺序)。显然，对于前一种处理方式，课堂教学的逻辑顺序更为明显，教学易于操控;而对于后一种处理方式，给学生和教师都留下了比较大的空间，教学将更为开放，课堂更具生成性，但同时也不可避免具有一定的不可操控性，对教师自身素质提出了更高的要求。

一般四边形的镶嵌问题，是这堂课地教学难点。如何突破，这是摆在老师们面前的一个课题。这里可以有多种方式:如，考虑到该镶嵌图案的探究对学生而言确实有难度，可以在学生一定的拼接活动的基础上"告诉"，或者借助现实生活中一些具体图形(如一些道路护坡的图片)直接"告诉";也可以引导学生关注三角形、平行四边形等不同的镶嵌图案之间的关系以及同一个镶嵌图案中各个多边形之间的变换关系，然后通过适当的变式揭示四边形的镶嵌问题(见参考案例)。在获得一般四边形的镶嵌图案(如甲图)之后，可能学生还有一些疑问，如四边形所构成的图案是"凹凸不平"的，如何铺满整个平面?为此，可以通过具体的拼接活动让学生获得进一步的直观感受;或者分析共顶点的四个四边形组成的"基本图案"(如乙图)，发现将"基本图案"中的两个三角形剪切后平移即可得到一个平行四边形(如丙图)，而平行四边形是可以镶嵌整个平面的，因此，这里"基本图案"的镶嵌相当于将平行四边形中剪切了部分移入另一个临近的平行四边形中。这样，不仅关注了什么图形能够镶嵌，而且关注了镶嵌图形的形成过程，可以为镶嵌图形的设计提供一些参考。

1.全等的任意三角形能镶嵌平面

把一些纸整齐地叠放好，用剪刀一次即可剪出多个全等的三角形.用这些全等的三角形可镶嵌平面.这是因为三角形的内角和是180°，用6个全等的三角形即可镶嵌出一个平面.如图1.

用全等的三角形镶嵌平面，镶嵌的方法不止一种，如图2.

2.全等的任意四边形能镶嵌平面。

仿上面的方法可剪出多个全等的四边形，用它们可镶嵌平面.这是因为四边形的内角和是360°，用4个全等的四边形即可镶嵌出一个平面.如图3.其实四边形的平面镶嵌可看成是用两类全等的三角形进行镶嵌.如图4.

3.全等的特殊五边形可镶嵌平面

圣地亚歌一位家庭妇女，五个孩子的母亲玛乔里·赖斯，对平面镶嵌有很深的研究，尤其对五边形的镶嵌提出了很多前所未有的结论.1968年克什纳断言只有8类五边形能镶嵌平面，可是玛乔里·赖斯后来又找到了5类五边形能镶嵌平面，在图5的五边形ABCDE中，∠B=∠E=90°，2∠A+∠D=2∠C+∠D=360°，a=e，a+e=d.图6是她于1977年12月找到的一种用此五边形镶嵌的方法.用五边形镶嵌平面，是否只有13类，还有待研究.

4.全等的特殊六边形可镶嵌平面

1918年，莱因哈特证明了只有3类六边形能镶嵌平面.图7是其中之一.在图7的六边形ABCDEF中，∠A+∠B+∠C=360°，a=d.

5.七边形或多于七边的凸多边形，不能镶嵌平面.

只有正三角形、正方形和正六边形可镶嵌平面，用其它正多边形不能镶嵌平面.

所有的方法:

用1种:(3，3，3，3，3，3)(4，4，4，4)(6，6，6);

用2种:(4，8，8)(3，12，12)(3，3，6，6)(3，3，3，3，6)(3，3，3，4，4)(*5，10，10)

用3种:(3，4，4，6)(4，6，12)(3，3，4，12)(3，10，15)(3，9，18)(3，8，24)(3，7，42)(*4，5，20)

其中的数字分别代表正多边形的边数。共有17种。

是枚举出来的。

证明不能用3种以上的多边形镶嵌:

因为若用4种，则内角和最小为60+90+108+120=378>360，(三角形、正方形、正五边形、正六边形)。

另外其中带星号的的两个(5,10,10)(3,7,42)是只能在一个点镶嵌，而不能在整个平面镶嵌。不带这两个，则是有15种方法。

例如:用正三角形和正六形的组合进行镶嵌.设在一个顶点周围有m个正三角形的角，有n个正六边形的角.由于正三角形的每个角是60°，正六边形的每个角是120°.所以有

m·60°+n·120°=360°，即m+2n=6.

这个方程的正整数解 或 可见用正三角形和正六边形镶嵌，有两种类型，一种是在一个顶点的周围有4个正三角形和1个正六边形，另一种是在一个顶点的周围有2个正三角形和2个正六边形.如图8、图9.