平方千米单位转换
1平方千米(1 km²)等于:
1,000,000平方米
10,000,000,000平方厘米
100公顷
10,000公亩
247.105381467英亩
100.83町
0.386 102平方英里
10,758,400平方英尺
1,550,000,000平方英寸
换算为km²:
1平方米=0.000 001km²
1平方厘米=0.000 000 000 1km²
1公顷=0.01km²
1公亩=0.000 1km²
1英亩=0.004 047km²
1町=0.009 917km²
1平方英里=2.589 988km²
1平方英尺=0.000 000 092 951km²
1平方英寸=0.000 000 000 645km²2100433B
平方千米造价信息
“平方千米”是比“公顷”还大的面积单位,计算较大的土地面积一般用“平方千米”做单位。例如,我国国土的陆地面积大约是960万平方千米。
平方千米单位转换常见问题
平方千米单位转换文献

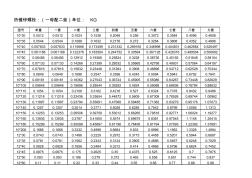 螺栓单位转换表
螺栓单位转换表
型号 单重 一套 二套 三套 四套 五套 六套 七套 八套 九套 10*30 0.0512 0.0512 0.1024 0.1536 0.2048 0.256 0.3072 0.3584 0.4096 0.4608 10*35 0.0544 0.0544 0.1088 0.1632 0.2176 0.272 0.3264 0.3808 0.4352 0.4896 10*40 0.057833 0.057833 0.115666 0.173499 0.231332 0.289165 0.346998 0.404831 0.462664 0.520497 10*45 0.061188 0.061188 0.122376 0.183564 0.244752 0.30594 0.367128 0.428316 0.489504 0.550692 10*50 0.06456 0.06456 0.12

 管材管件规格及公制和英制单位转换
管材管件规格及公制和英制单位转换
管材管件规格及公制和英制单位转换
《千米级斜拉桥:结构体系、性能与设计》针对千米级斜拉桥结构体系、性能和设计方法等问题,以主跨1088m苏通大桥为基础,拓展到主跨1308m、1500m、1800m等跨度的千米级斜拉桥,研究了千米级斜拉桥设计理论和方法、结构体系与关键参数、风作用特性与结果响应、抗震设计、船舶撞击作用和设计方法、汽车作用下结构性能、弹塑性稳定性能、极端作用特性及设计方法等。《千米级斜拉桥:结构体系、性能与设计》系统解决了千米级斜拉桥设计理论、方法、参数、标准方面关键问题,可为同类桥型的建设提供参考和借鉴。
《千米级斜拉桥:结构体系、性能与设计》可供从事桥梁设计、施工及相关研究人员阅读,也可供高等学校相关专业研究生和高年级本科生阅读。
1 斜拉桥跨径发展和关键问题
1.1 斜拉桥的发展历程
1.2 斜拉桥基本结构体系
1.3 斜拉桥跨径发展的性能演变
1.4 千米级斜拉桥设计的关键问题
2 千米级斜拉桥设计理论与方法
2.1 寿命周期设计理论和基本过程
2.2 基于性能的设计方法及其应用
2.3 极端作用及其组合设计方法
3 千米级斜拉桥结构体系与关键参数影响
3.1 千米级斜拉桥合理结构体系
3.2 千米级斜拉桥关键参数影响分析
3.3 千米级斜拉桥结构方案设计
4 千米级斜拉桥风作用特性及结构响应
4.1 斜拉索静风风荷载特性研究
4.2 桥塔气动力研究
4.3 非线性静动力响应研究
4.4 千米级斜拉桥风荷载及合理体系研究
4.5 千米级斜拉桥风致振动响应特性试验研究
4.6 千米级斜拉桥安全行车风速
5 千米级斜拉桥抗震设计
5.1 国内外桥梁抗震设计规范比较研究
5.2 部分已建大跨度缆索支撑桥梁的抗震设计
5.3 千米级斜拉桥的地震反应特性及简化计算
5.4 跨度增大对千米级斜拉桥地震反应的影响
5.5 群桩基础的非线性地震反应分析
6 千米级斜拉桥船舶撞击作用和设计方法
6.1 大跨径桥梁船撞事故
6.2 船撞作用下非线性动力响应特性
6.3 船撞力实用计算方法
7 千米级斜拉桥在汽车作用下的结构性能
7.1 各国规范汽车作用比较研究
7.2 汽车活载计算分析方法适用性分析
7.3 千米级斜拉桥汽车作用非线性响应特性
7.4 千米级斜拉桥汽车作用简化计算方法
7.5 千米级斜拉桥车辆动力放大系数
8 千米级斜拉桥弹塑性稳定性能研究
8.1 桥梁稳定问题及其分析方法
8.2 千米级斜拉桥弹性稳定分析
8.3 千米级斜拉桥弹塑性稳定特性
8.4 弹塑性稳定安全系数的合理取值
9 千米级斜拉桥极端作用特性及设计方法
9.1 千米级斜拉桥抗火设计
9.2 千米级斜拉桥拉索系统强健性设计
9.3 千米级斜拉桥龙卷风作用设计
参考文献2100433B
平方R 英语为:R square。缩写为:R2。时常用作R平方。通过基准数据描述证券价格变动的参数。固定收益证券的参照基准为政府短期债券;股票多采用标准普尔500指数。平方R值从0-100,当数值为100时,表示某证券价格变化与基准值完全一致。平方R值越高,越需要与贝塔(beta)值配套使用。如某债券平方R 接近100,同时贝塔值低于1,该债券很可能是高风险债券。当平方R值较低时,可以忽略贝塔值。
- 相关百科
- 相关知识
- 相关专栏
- 平方厘米
- 政绩工程的原因探析与治理对策
- 半拉子工程
- Excel专家实战问答800问
- 沈阳和新套管有限公司
- 西安西电高压套管有限公司
- 工程技术模型
- 威海新城建设有限公司
- 安徽富煌建筑工业有限公司
- 工程制图简明教程
- Photoshop 6.0 从入门到精通
- ACROBAT 6电子文件轻松上手
- CAD工程制图:AUTOCAD 2008软件应用
- CAD/CAM应用技术——UG NX6.0
- CAD工程制图:AUTOCAD 2006
- AutoCAD2014工程绘图教程
- 云南省氯碱PVC行业清洁生产合格单位评价指标体系
- 云南省机关事业单位编制外人员劳动合同书(修改后)
- 中国建设工程鲁班奖(国家优质工程)申报单位承诺书
- 招标选择政府投资工程委托代建单位中报价文件的评选
- 有粘结预应力技术在高层建筑转换梁结构施工中的应用
- 中国室内装饰设计施工单位资质等级管理办法及申请表
- 关于高速公路运营管理单位有效实施全面预算管理
- 关于当前农村水利基层单位配套改革财务管理几点思考
- 工程施工安全检查用表监理单位专用与施工单位内业专用
- 关于规范单位工程施工组织设计内容编写通知
- 关于国有水利工程建设单位自用固定资产核算一点思考
- 关于加强生产经营单位生产安全事故应急预案管理工作
- 工程监理单位项目总监(总监代表)带班生产情况记录表
- 工程量清单报价中投标单位企业最低成本测算方法
- 光伏区电气设备安装单位工程质量验收评定表收集资料
- 改进输电线路工程单位造价指标