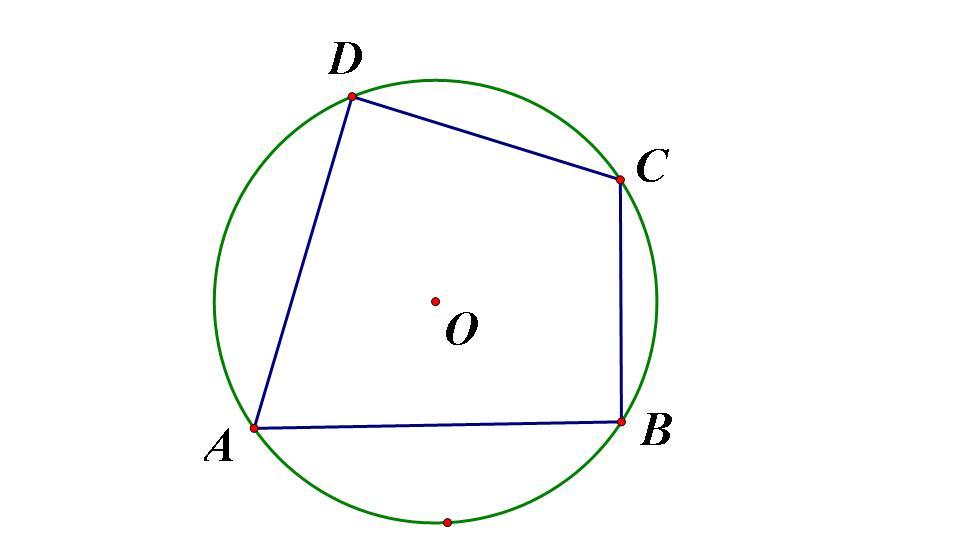
内接四边形对角互补
内接四边形对角互补(Inscribed quadrilateral diagonal complementary)是指圆的内接四边形的对角互补,特点是任意一个外角等于它的内对角。
内接四边形对角互补基本信息
| 中文名称 | 内接四边形对角互补 | 外文名称 | Inscribed quadrilateral diagonal complementary |
|---|---|---|---|
| 特点 | 任意一个外角等于它的内对角 | 依据 | 圆周角等于圆心角一半 |
内接四边形对角互补:圆的内接四边形的对角互补,并且任意一个外角等于它的内对角
四个点在圆上四边形是圆的内接四边形.圆内接四边形对角互补,外角等于它的内对角
【证明】
首先证∠A+∠C=180
如图所示,连接DO, BO. 设∠BOD为360°-θ
∵圆周角等于所对的圆心角的一半
∴∠C=1/2∠BOD,
同理,∠A=1/2θ
∴∠A+∠C=1/2*360=180,即两角互补。
同理可证∠ABC+∠ADC=180.所以对角互补。
证毕
依据:
①圆周角等于圆心角一半
②圆周角等于360°
内接四边形对角互补造价信息
内接四边形对角互补常见问题
-
采用正玄定理和余弦定理A/sina=B/sinb=c/sinc和A平方=B平方+C平方-2BC*coma
-
四边形面积必须要知道角度。
-
四边形有两条对角线,五边形有五条对角线,六边形有九条对角线
内接四边形对角互补文献

 无对角线四边形建筑方格图的精度估算
无对角线四边形建筑方格图的精度估算
无对角线四边形法是建立建筑方格网中二级网的有效方法。对于建筑方格网来说,重要的方面之一是可以评定网中任意元素的精度。本文就无对角线四边形网的必要测角精度,方位角所需精度以及边长与点位精度估算进行探讨。

 平行四边形设计
平行四边形设计
平行四边形设计 及反思 教学内容: 教材第 97—99页例 1、例 2,课堂活动,练习二十第 1—3题。 课时目标: 1.能够从图中全面感知平行四边形现象,体会平行四边形在生活情景中的 存在。 2.通过观察、操作等活动,认识平行四边形的一些特征。 3.经历探索平行四边形的过程, 了解它的基本特征, 进一步发展空间观念。 教学重点: 通过观察、操作等活动,认识平行四边形的一些特征。 教学难点: 经历探索平行四边形的过程,了解它的基本特征。 教学用具: 课件,展台 板书设计 平行四边形 两组对边分别平行的四边形_平行四边形 特性:易变形 特征:两组对边分别相等 两组对角分别相等 四个内角的和是 360o 教学流程 一. 引入 1、揭示课题 同学们,我们知道 由 3条线段围成的图形叫做三角形,那老师给 4条线段 你有可能围成什么图形?(四边形、长方形、正方形、梯形、棱形平行四边形) 生活中哪些
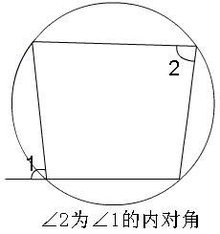
内对角定义
四边形外角的邻补角的对角即为此外角的内对角(内对角相对于四边形外角而言)。
圆内接四边形定理
圆内接四边形:对角互补,外角与内对角相等。
当四边长度给定时,四边形面积的最大值
设a b c d=2p,公式(1)能改写成更对称更完整且便于记忆的形式
这个关于a、b、c、d具有对称形式的公式还告诉我们:面枳的最大值与给定边的次序无关,仅由给定的边长a、b、c、d惟一确定。
假如四辺形ABCD的边长中有一边的长度逐渐缩短而最后趋于零,譬如DA=d=0,此吋,四边形退化为三角形,任何三角形都内接于圆,故得三角形面积
公式(1):
内接线是连接电动机、开关等工具内部电路并包封在外壳中的导线。
内接线
internal wiring
- 相关百科
- 相关知识
- 相关专栏
- 海绵铁压块机
- 料封泵
- 房屋安全鉴定案例
- 起动机
- MSZ160-8八孔盘转式压砖机
- 闭孔海绵橡胶
- 钢筋连接套筒生产工艺
- 双齿辊式粗破碎煤机
- 旋滚式磨粉机
- 海绵城市建设技术指南
- 正泰稳压器
- JK系列矿井提升机
- 涡旋式流体机械与涡旋压缩机
- 计算机辅助船体建造
- 和风家具
- 压下蜗杆传动
- 既有广大铁路低净空隧道内接触网悬挂方案设计选取
- 基于图像处理单张纸胶印机对角线套准及自动控制系统
- PWM整流器在多能互补独立电力系统示范工程中的应用
- PWM整流器在多能互补独市电力系统示范工程中的应用
- 太阳能风光互补系统在数字化航道船联网工程中的应用研究
- 户内接地母线敷设
- pic18f6720的风光互补路灯控制器设计
- 单片机的太阳能路灯市电互补逆变光伏控制器设计
- 内接价格
- 安徽重点项目阜阳农光互补光伏发电项目可行性研究报告
- 变配电室及电气竖井内接地干线敷设检验批质量验收记录
- 工程建设监理与业主方项目管理衔接和互补问题的思考
- 光电互补路灯控制器与太阳能路灯控制器有何区别
- 风光互补发电系统安装与调试赛项规程
- 30MW农光互补光伏发电项目可行性研究报告
- 10kV小车式封闭开关柜内接头发热原因分析及预防