粒子空间分布spatial distribution c}f species电离辐射穿透物质时在物质中产生能量较高的原初活性粒子:电子、离子和激发分子。它们在物质中分布很不均匀,主要分布在人射粒子径迹附近,其密度与人射粒子种类、能量有关。低能次级电子在空气中产生很多刺迹,离子和激发分子从刺迹小区向外扩散,最终可能形成均匀分布的状态。了解粒子空问分布对研究辐射化学反应机制卜分重要。2100433B
粒子空间分布造价信息
粒子空间分布常见问题
-
你好,房子空间利用的话,,如果房子足够高,可利用其多余的高度隔出天花板夹层,加上折叠梯作为储藏室之用。挑高的房子更可做出夹层楼板,多出一至两个房间。
-
横铺的地板房间显得开阔,视觉感官较好。全铺的木地板铺设前不一定从门口开始铺,要综合考虑客厅、餐厅和过道的关系,选择一条主轴线(例如电视背景墙的那方墙),向轴线两侧铺设,这样裁切的地板较少,损耗可减少约...
-
1、小空间要使用“轻装修”原则 小户型装修一般都是采用“轻装修”的原则,小房间如果到处都是柜子,相对的却也减少了生活的空间。与其如此,不如把装修的钱拿来买一些比较好一点的家具。...
粒子空间分布文献

 基于Krylov子空间的微混合器宏模型设计与仿真
基于Krylov子空间的微混合器宏模型设计与仿真
获得宏模型是微混合器设计与仿真的关键。将Navier-Stokes方程和对流扩散方程用有限元方法进行离散化处理,应用Krylov子空间的Arnoldi过程对得到的微分-代数方程组降阶处理,提取出宏模型。仿真结果表明,经过降阶处理得到的宏模型保证了微混合器的输出精度,降低了计算复杂度。

 基于分形理论的地质灾害空间分布特征研究
基于分形理论的地质灾害空间分布特征研究
在诸如崩塌、滑坡等地质灾害的处理过程中,网格法往往会对空间分布的分形特征进行研究和分析,然后理论才形成。在以往的地质灾害样本数据分析中,地质专家得出D=0.4108是滑坡的分形分维值,崩塌的分形分维值D=0.3632,其分形特征从分析来看相对较为明显,自相似性也具有研究意义。从数据的分析来看,崩塌分形分维值明显低于滑坡的分形分维值,由此看出,从空间分布来讲,崩塌灾害的复杂程度不及滑坡。
空间分布指水生生物在水域空间的分布。
- 中文名称
- 空间分布
- 英文名称
- spatial distribution
- 定 义
- 水生生物在水域空间的分布。
- 应用学科
- 水产学(一级学科),水产基础科学(二级学科)
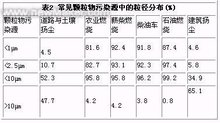
大气气溶胶粒子谱分布
气溶胶粒子的谱分布是指对应于不同半径的气溶胶粒子浓度的分布。
一、气溶胶粒子的分类按尺度大小对气溶胶粒子的分类(半径用等效半径)爱根核(半径r10μm飘尘:直径D海洋上城市乡村低空高空阴天晴天晚间白天冬季夏季见图气溶胶粒子浓度的垂直分布:对流层中气溶胶粒子浓度随高度按指数减小,对流层顶达到最小。平流层中气溶胶粒子浓度又有些增加,在20km左右出现一个气溶胶层。2.5.2气溶胶粒子的来源气溶胶粒子的来源很广,有自然的,也有人为的一、土壤、岩石风化及火山喷发的尘埃如1991.6非律宾皮纳图博强火山爆发
二、烟尘及工业粉尘人类活动产生的气溶胶粒子的浓度有明显的日变化:◇清晨,浓度最大;◇中午前后,浓度最小◇黄昏,浓度又增加;◇夜间,浓度再次减小。
三、海沫破裂干涸成核海沫破裂产出海盐水滴,蒸发干涸形成巨核和爱根核。
四、气-粒转化爱根核由大气中微量气体转化而来。如so2经光化学氧化作用,高温下能生成硫酸盐微滴,蒸发后成为硫酸盐质点。
五、微生物、孢子、花粉等有机物质点。
六、宇宙尘埃,如流星2.5.3气溶胶粒子在大气过程中的作用一、在云雾降水中的作用气溶胶粒子起着凝结核、冰核、凝冻核、凝华核的作用,使云雾滴能够产生并长大,形成云雾降水。
与卡尔曼滤波(Kalman Filter)相比较
粒子滤波(PF: Particle Filter)的思想基于蒙特卡洛方法(Monte Carlo methods),它是利用粒子集来表示概率,可以用在任何形式的状态空间模型上。其核心思想是通过从后验概率中抽取的随机状态粒子来表达其分布,是一种顺序重要性采样法(Sequential Importance Sampling)。简单来说,粒子滤波法是指通过寻找一组在状态空间传播的随机样本对概率密度函数进行近似,以样本均值代替积分运算,从而获得状态最小方差分布的过程。这里的样本即指粒子,当样本数量N→∝时可以逼近任何形式的概率密度分布。
尽管算法中的概率分布只是真实分布的一种近似,但由于非参数化的特点,它摆脱了解决非线性滤波问题时随机量必须满足高斯分布的制约,能表达比高斯模型更广泛的分布,也对变量参数的非线性特性有更强的建模能力。因此,粒子滤波能够比较精确地表达基于观测量和控制量的后验概率分布,可以用于解决SLAM问题。
粒子滤波的应用
粒子滤波技术在非线性、非高斯系统表现出来的优越性,决定了它的应用范围非常广泛。另外,粒子滤波器的多模态处理能力,也是它应用广泛的原因之一。国际上,粒子滤波已被应用于各个领域。在经济学领域,它被应用在经济数据预测;在军事领域已经被应用于雷达跟踪空中飞行物,空对空、空对地的被动式跟踪;在交通管制领域它被应用在对车或人视频监控;它还用于机器人的全局定位。
粒子滤波的缺点
虽然粒子滤波算法可以作为解决SLAM问题的有效手段,但是该算法仍然存在着一些问题。其中最主要的问题是需要用大量的样本数量才能很好地近似系统的后验概率密度。机器人面临的环境越复杂,描述后验概率分布所需要的样本数量就越多,算法的复杂度就越高。因此,能够有效地减少样本数量的自适应采样策略是该算法的重点。另外,重采样阶段会造成样本有效性和多样性的损失,导致样本贫化现象。如何保持粒子的有效性和多样性,克服样本贫化,也是该算法研究重点。
- 相关百科
- 相关知识
- 相关专栏
- 用于制冷系统稳定运行时制冷剂分布测试的新方法
- 中国铁道建筑总公司地下空间安全管理知识培训
- 异构分布式防火墙与入侵检测联动构架的通信机制
- 居室空间设计
- 展览建筑的空间布局类型——以云南省博物馆为例
- 新型空间梁单元及其在梁杆结构稳定分析中的应用
- 伊拉克美索不达米亚平原软土分布特征及工程性质分析
- 应用Block模型高大空间分层空调的温度分布
- 应用于分布式光纤拉曼温度传感器的温度补偿电路
- 园林植物空间营造
- 应用螺杆钻定向钻探技术在复杂地层施工空间型定向孔
- 关于氮气等温吸脱附计算比表面积、孔径分布若干说明
- 公路隧道Ⅴ级围岩初支型钢支架受力分布及动态变化
- 各地插头插座分布(东亚、东南亚、南亚、中东、非洲)
- 关于城市务工人员居住空间改造设计
- 公共建筑及市政配套工程在地下空间中一体化设计