临界力分析临界力的步骤
1、分析临界状态:
一般采用极端分析法,即把问题中的物理量推向极值,就会暴露出物理过程,常见的有A.发生相对滑动;B.绳子绷直;C.与接触面脱离。
所谓临界状态一般是即将要发生质变时的状态,也是未发生质变时的状态。此时物体所处的运动状态常见的有:A.平衡状态;B.匀变速运动;C.圆周运动等。
2、找出临界条件:
上述临界状态其对应临界条件是:
(1)相对滑动与相对静止的临界条件是静摩擦力达最大值;
(2)绳子松弛的临界条件是绳中拉力为零;
(3)相互接触的两个物体将要脱离的临界条件是相互作用的弹力为零。
3、列出状态方程:
将临界条件代到状态方程中,得出临界条件下的状态方程。
4、联立方程求解:
有些临界问题单独临界条件下的状态方程不能解决问题,则需结合其他规律联立方程求解。 2100433B
临界力造价信息
欧拉公式只有在弹性范围内才是适用的。为了判断压杆失稳时是否处于弹性范围,以及超出弹性范围后临界力的计算问题,必须引入临界应力及柔度的概念。
压杆在临界力作用下,其在直线平衡位置时横截面上的应力称为临界应力,压杆在弹性范围内失稳时,则临界应力为柔度与长细比的比值。
表1为常用材料的应力计算值:
| 材 料 |
|||
| A3钢 |
304 |
1.12 |
102 |
| 优质碳钢 |
461 |
2.568 |
95 |
| 铸 铁 |
332.2 |
1.454 |
70 |
| 木 材 |
28.7 |
0.190 |
80 |
杆件所受压力逐渐增加到某个限度时,压杆将由稳定状态转化为不稳定状态。这个压力的限度称为临界力。它是压杆保持直线稳定形状时所能承受的最小压力。
为了计算压杆的稳定性,就要确定临界力的大小。通过实验和理论推导,压杆临界力与各个因素有关:
(1)压杆的材料,临界力与材料的弹性模量E成正比;
(2)压杆横截面的形状和尺寸,临界力与压杆横截面的轴惯性矩成正比;
(3)压杆的长度,临界力与长度的平方成反比;
(4)压杆两端的支座形式有关,用支座系数表示。
当已知压杆的材料、尺寸和支座形式时,即可由欧拉公式求得临界力根据欧拉公式,若要提高细长杆的稳定性,可从下列几方面来考虑:
(1)合理选用材料:
临界力与弹性模量E成正比。钢材的E值比铸铁、铜、铝的大,压杆选用钢材为宜。合金钢的E值与碳钢的E值近似,细长杆选用合金钢并不能比碳钢提高稳定性,但对短粗杆,选用合金钢可提高工作能力。
(2)合理选择截面形状:
临界力与截面的轴惯性矩成正比。应选择大的截面形状,如圆环形截面比圆形截面合理,型钢截面比矩形截面合理。并且尽量使压杆横截面对两个互相垂直的中性轴的惯性矩相近。
(3)减少压杆长度:
临界力与杆长平方成反比。在可能的情况下,减小杆的长度或在杆的中部设置支座,可大大提高其稳定性。
(4)改善支座形式:
临界力与支座形式有关。固定端比铰链支座的稳定性好,钢架的立柱,其柱脚与底板的联系形式,能提高立柱受压时的稳定性。
临界力分析临界力的步骤常见问题
-
任何一种物质都存在三种相态----气相、液相、固相。三相呈平衡态共存的点叫三相点。液、气两相呈平衡状态的点叫临界点。在临界点时的温度和压力称为临界温度和临界压力。
-
各种气体都有一个特殊的温度,在这个温度以上,无论怎样增大压强也不能使气体液化,这个温度叫做临界温度。临界温度时,使气体液化所需的压力称为临界压力。由于氨的临界温度为132.4℃、临界压力为11.298...
-
物质处于临界状态时的压力(压强)。就是在临界温度时使气体液化所需要的最小压力。也就是液体在临界温度时的饱和蒸气压。在临界温度和临界压力下,物质的摩尔体积称为临界摩尔体积。临界温度和临界压力下的状态称为...
压杆临界力
1、同一长度的压杆,截面积及材料均相同,仅两端支承条件不同,则一端固定,一端自由杆的临界力最小。
2、受压杆在下列支承情况下,若其他条件相同,临界力最大的是两端固定
3、受压物件,两端铰支,临界力为50kN,若将物件改为两端固定,则其临界力为500kN。
P'=π2EI/L2 即:P等于3.14的平方乘以E 和I 与L的平方之比。
式子中P表示临界力;E表示弹性模量; I 表示惯性矩
临界力Pij的大小与下列因素有关:
1、压杆的材料:钢柱的P比木柱大,因为钢柱的弹性模量E大。
2、压杆的截面形状与大小:截面大不易失稳,因为惯性矩大。
3、压杆长度L:压杆长度大,P临界力小,易失稳。
临界力分析临界力的步骤文献

 中心配索式预应力钢管混凝土轴压构件临界力理论分析方法
中心配索式预应力钢管混凝土轴压构件临界力理论分析方法
本文利用有限元法、共轭法对具有侧向水平弹性约束的轴心受压构件临界力的计算方法进行了分析和推导,所建立的理论计算方法概念明确、计算简便.为进行中心配索式预应力钢管混凝土结构的轴压构件临界力计算奠定了理论基础。

 双层地基临界深度的数值分析
双层地基临界深度的数值分析
双层地基临界深度的数值分析——基于极限平衡滑移线理论,采用差分算法编制了针对包头地区普遍存在的双层地基数值计算程序,由程序分析了无重土和有重土中临界深度与土内摩擦角的关系,给出了考虑土重时土体的临界深度拟合公式,并经对比是可行的.
(1)细长受压杆件,承载力远低于其强度核算指标;
(2)细长受压杆件的长细比是影响稳定临界力的综合因素;
(3)注意相同杆件、不同支撑状况下稳定临界力的排序。
某受压钢筋混凝土柱,高3.6m,两端铰支,其临界力为50kN,若将此构件改为两端固定,则其临界力为()kN.
A、50
B、100
C、150
D、200
【正确答案】D
【答案解析】本题考查的是杆件稳定的基本概念。根据公式:Pij=π2EI/l02,两端铰支时,l0=l,两端固定时,l0=0.5l可得当调整为两端固定时临界力变为原来的4倍,50×4=200。参见教材P3。
受压构件,一端固定,一端自由,其临界力为50KN,若受压构件弹性模量E增加一倍时,则其临界力为()KN。
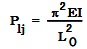
A、50
B、100
C、150
D、800
【正确答案】B
【答案解析】本题考查的是杆件稳定的基本概念。弹性模量增加一倍时,临界力增加一倍,50×2=100kN。参见教材P3。
- 相关百科
- 相关知识
- 相关专栏
- 基于压电堆驱动器的喷嘴挡板式气体控制阀
- 磷铵技术改造五大磷肥工程的建议
- 以大豆油多元醇制备的硬质聚氨酯泡沫塑料的性能
- 逆变TIG焊机接触引弧电路的设计(引弧电路)
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 中国吹制玻璃行业市场前景分析预测年度报告(目录)
- 可替代现有隔热保温材料的新型材料
- 中国电力井盖行业市场前景分析预测年度报告(目录)
- 以贯穿项目为核心载体的建筑工程技术专业素材库建设
- 多逆变器太阳能光伏并网发电系统的组群控制方法
- 影响萘高效减水剂与普通硅酸盐水泥适应性的关键因素
- 在全县非煤矿山和危化企业安全生产工作会议上的讲话
- 中国工程造价咨询业的发展趋势
- 支持并行工程和智能CAPP的制造资源建模技术
- 中国轨道射灯行业市场前景分析预测年度报告
- 中共重庆市委重庆市人民政府关于建设平安重庆的决定