临界力
临界力基本信息
| 中文名 | 临界力 | 应用领域 | 机械,建筑 |
|---|---|---|---|
| 公 式 | P'=π2EI/L2 | 影响因素 | 杆件的材料、长度、截面形状尺寸以及杆端的约束情况 |
| 学 科 | 建筑工程结构力学 | 代 表 | 压杆临界力 |
杆件所受压力逐渐增加到某个限度时,压杆将由稳定状态转化为不稳定状态。这个压力的限度称为临界力。它是压杆保持直线稳定形状时所能承受的最小压力。
为了计算压杆的稳定性,就要确定临界力的大小。通过实验和理论推导,压杆临界力与各个因素有关:
(1)压杆的材料,临界力与材料的弹性模量E成正比;
(2)压杆横截面的形状和尺寸,临界力与压杆横截面的轴惯性矩成正比;
(3)压杆的长度,临界力与长度的平方成反比;
(4)压杆两端的支座形式有关,用支座系数表示。
当已知压杆的材料、尺寸和支座形式时,即可由欧拉公式求得临界力根据欧拉公式,若要提高细长杆的稳定性,可从下列几方面来考虑:
(1)合理选用材料:
临界力与弹性模量E成正比。钢材的E值比铸铁、铜、铝的大,压杆选用钢材为宜。合金钢的E值与碳钢的E值近似,细长杆选用合金钢并不能比碳钢提高稳定性,但对短粗杆,选用合金钢可提高工作能力。
(2)合理选择截面形状:
临界力与截面的轴惯性矩成正比。应选择大的截面形状,如圆环形截面比圆形截面合理,型钢截面比矩形截面合理。并且尽量使压杆横截面对两个互相垂直的中性轴的惯性矩相近。
(3)减少压杆长度:
临界力与杆长平方成反比。在可能的情况下,减小杆的长度或在杆的中部设置支座,可大大提高其稳定性。
(4)改善支座形式:
临界力与支座形式有关。固定端比铰链支座的稳定性好,钢架的立柱,其柱脚与底板的联系形式,能提高立柱受压时的稳定性。
临界力造价信息
欧拉公式只有在弹性范围内才是适用的。为了判断压杆失稳时是否处于弹性范围,以及超出弹性范围后临界力的计算问题,必须引入临界应力及柔度的概念。
压杆在临界力作用下,其在直线平衡位置时横截面上的应力称为临界应力,压杆在弹性范围内失稳时,则临界应力为柔度与长细比的比值。
表1为常用材料的应力计算值:
| 材 料 |
|||
| A3钢 |
304 |
1.12 |
102 |
| 优质碳钢 |
461 |
2.568 |
95 |
| 铸 铁 |
332.2 |
1.454 |
70 |
| 木 材 |
28.7 |
0.190 |
80 |
P'=π2EI/L2 即:P等于3.14的平方乘以E 和I 与L的平方之比。
式子中P表示临界力;E表示弹性模量; I 表示惯性矩
临界力Pij的大小与下列因素有关:
1、压杆的材料:钢柱的P比木柱大,因为钢柱的弹性模量E大。
2、压杆的截面形状与大小:截面大不易失稳,因为惯性矩大。
3、压杆长度L:压杆长度大,P临界力小,易失稳。
临界力常见问题
-
任何一种物质都存在三种相态----气相、液相、固相。三相呈平衡态共存的点叫三相点。液、气两相呈平衡状态的点叫临界点。在临界点时的温度和压力称为临界温度和临界压力。
-
各种气体都有一个特殊的温度,在这个温度以上,无论怎样增大压强也不能使气体液化,这个温度叫做临界温度。临界温度时,使气体液化所需的压力称为临界压力。由于氨的临界温度为132.4℃、临界压力为11.298...
-
百度知道内容: 亚临界萃取 【亚临界萃取】(Sub-critical fluid extraction technology) 亚临界萃取是利用亚临界流体作为萃取剂, 在密闭、无氧。低压的压力容器内,...
压杆临界力
1、同一长度的压杆,截面积及材料均相同,仅两端支承条件不同,则一端固定,一端自由杆的临界力最小。
2、受压杆在下列支承情况下,若其他条件相同,临界力最大的是两端固定
3、受压物件,两端铰支,临界力为50kN,若将物件改为两端固定,则其临界力为500kN。
1、分析临界状态:
一般采用极端分析法,即把问题中的物理量推向极值,就会暴露出物理过程,常见的有A.发生相对滑动;B.绳子绷直;C.与接触面脱离。
所谓临界状态一般是即将要发生质变时的状态,也是未发生质变时的状态。此时物体所处的运动状态常见的有:A.平衡状态;B.匀变速运动;C.圆周运动等。
2、找出临界条件:
上述临界状态其对应临界条件是:
(1)相对滑动与相对静止的临界条件是静摩擦力达最大值;
(2)绳子松弛的临界条件是绳中拉力为零;
(3)相互接触的两个物体将要脱离的临界条件是相互作用的弹力为零。
3、列出状态方程:
将临界条件代到状态方程中,得出临界条件下的状态方程。
4、联立方程求解:
有些临界问题单独临界条件下的状态方程不能解决问题,则需结合其他规律联立方程求解。 2100433B
临界力文献

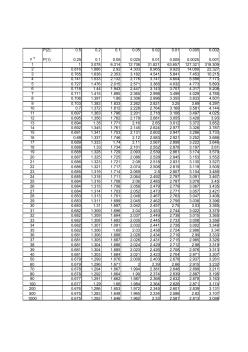 t检验(t-test)临界值表(临界置信水平)
t检验(t-test)临界值表(临界置信水平)
P(2): 0.5 0.2 0.1 0.05 0.02 0.01 0.005 0.002 P(1): 0.25 0.1 0.05 0.025 0.01 0.005 0.0025 0.001 1 1 3.078 6.314 12.706 31.821 63.657 127.321 318.309 2 0.816 1.886 2.92 4.303 6.965 9.925 14.089 22.327 3 0.765 1.638 2.353 3.182 4.541 5.841 7.453 10.215 4 0.741 1.533 2.132 2.776 3.747 4.604 5.598 7.173 5 0.727 1.476 2.015 2.571 3.365 4.032 4.773 5.893 6 0.718 1.44 1.943 2.447 3.143 3.707 4.317 5.208 7

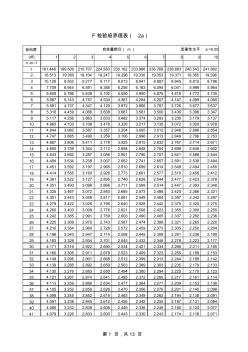 F检验临界表
F检验临界表
自由度 (df) 1 2 3 4 5 6 7 8 9 10 n -m-1 1 161.448 199.500 215.707 224.583 230.162 233.986 236.768 238.883 240.543 241.882 2 18.513 19.000 19.164 19.247 19.296 19.330 19.353 19.371 19.385 19.396 3 10.128 9.552 9.277 9.117 9.013 8.941 8.887 8.845 8.812 8.786 4 7.709 6.944 6.591 6.388 6.256 6.163 6.094 6.041 5.999 5.964 5 6.608 5.786 5.409 5.192 5.050 4.950 4.876 4.818 4.772 4.735 6 5.987 5.143 4.757 4.
(1)细长受压杆件,承载力远低于其强度核算指标;
(2)细长受压杆件的长细比是影响稳定临界力的综合因素;
(3)注意相同杆件、不同支撑状况下稳定临界力的排序。
某受压钢筋混凝土柱,高3.6m,两端铰支,其临界力为50kN,若将此构件改为两端固定,则其临界力为()kN.
A、50
B、100
C、150
D、200
【正确答案】D
【答案解析】本题考查的是杆件稳定的基本概念。根据公式:Pij=π2EI/l02,两端铰支时,l0=l,两端固定时,l0=0.5l可得当调整为两端固定时临界力变为原来的4倍,50×4=200。参见教材P3。
受压构件,一端固定,一端自由,其临界力为50KN,若受压构件弹性模量E增加一倍时,则其临界力为()KN。
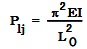
A、50
B、100
C、150
D、800
【正确答案】B
【答案解析】本题考查的是杆件稳定的基本概念。弹性模量增加一倍时,临界力增加一倍,50×2=100kN。参见教材P3。
- 相关百科
- 相关知识
- 相关专栏
- 中国电科院电力安全工作规程专项培训
- 圆形截面钢筋混凝土受弯构件正截面承载力的简化计算
- 在线期刊——制冷空调与电力机械竞争的新着力点
- 圆形钢筋混凝土截面大偏压构件正截面承载力的简算法
- 中电建协发布中国电力优质工程奖评选通知
- 有关水电站小开度甩负荷工况水击压力骤升问题
- 张家口清水河建设桥临时支架及河道行洪能力计算分析
- 岳阳洞庭湖大桥50m跨连续箱形梁桥三向预应力施工
- 在面内压力作用下点腐蚀低碳钢板的非线性有限元分析
- 在工程制图课程教学中培养学生创造性思维能力的探索
- 有粘结预应力结构施工过程中的应力损失控制技术
- 应力波无损检测技术及其在木结构古建筑保护中的应用
- 中国国际航空公司北京市内货运中心框架梁预应力施工
- 有粘结预应力混凝土空心无梁楼盖结构设计分析与
- 振弦式锚杆应力计在腾龙桥一级水电站左岸边坡的应用
- 中国水利电力对外公司中标毛里求斯巴加泰勒大坝工程