(1) 定义: 范围(0 ,90]
(2) 作法:
a.平移法:在异面直线中的一条直线上选择“特殊点”,作另一条直线的平行线,常常利用中位线或成比例线段引平行线。
b.补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等。
范围:[0,90]
作法:作出直线和平面所成的角,关键是做垂线,找射影
空间角造价信息
从一条直线出发的两个半平面所组成的图形。二面角的大小用它的平面角来度量。
平面角的做法:a.定义法
b.三垂线定理及其逆定理法
c.垂面法
1. 空间角的计算方法都是转化为平面角计算。要充分挖掘图形的性质,寻求平行关系,比如利用“中点”等性质,直线与平面所称的角是平面的一条斜线和它在平面内的射影所成的锐角,我们往往在斜线上取一点向平面引垂线,以形成由平面的斜线、垂线及斜线在在平面上的射影组成的直角三角形。
2. 作二面角的平面角的方法:
a.定义法:在棱上取一点,过这点在两个平面内分别引棱的垂线,这两条射线所称的角,就是二面角的平面角。
b.三垂线定理及逆定理法:自二面角的一个面上一点向另一面引垂线,再由垂足向棱作垂线得到棱上的点,该点与面上一点连线,和该点与垂足连线所夹的角既未二面角的平面角。
c.作垂面法:自空间一点作与棱垂直的平面,截二面角得两条射线,所成角即为二面角的平面角。
3.求角的一般步骤 找出或作出有关的平面角 证明它符合意义 归到某一三角形中进行计算2100433B
空间角概念常见问题
-
从广义上可以把商业空间定义为:所有与商业活动有关的空间形态。从狭义上则可以把商业空间理解为:当前社会商业活动中所需的空间,即实现商品交换、满足消费者需求、实现商品流通的空间环境。其实就是狭义的概念理解...
-
餐饮空间是食品生产经营行业通过即时加工制作、展示销售等手段,向消费者提供食品和服务的消费场所。它包括餐馆、小吃店、快餐店、食堂等。餐馆(又叫酒店,酒家、酒楼、饭店,饭庄等)指以饭菜(包括中餐、西餐、日...
空间角概念文献

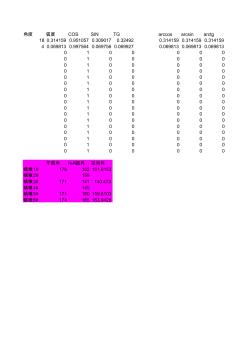 镇墩内钢管弯头空间角计算
镇墩内钢管弯头空间角计算
角度 弧度 COS SIN TG arccos arcsin arctg 18 0.314159 0.951057 0.309017 0.32492 0.314159 0.314159 0.314159 4 0.069813 0.997564 0.069756 0.069927 0.069813 0.069813 0.069813 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0

 压力供水管道工程设计中空间角的计算
压力供水管道工程设计中空间角的计算
在给水、中水等压力供水管道工程中,经常会遇到管道相对于绘图平面的空间转折,为降低能耗、节约投资、优化施工,如何将平面转角和竖向转角合二为一,快速准确地求得实际空间角,成为设计工作的重难点。详细阐述了作图法和公式法2种获得空间角的方法,并通过案例验证了公式法的适用性和简便性,对提高工程设计水平和工程经济效益将起到积极作用。
1.空间角的定义体现了空间问题平面化的数学思想。把空间的角转化为相交直线(如异面直线所成角、直线与平面所成角)或两条射线(如二面角的平面角)所成角。
2.空间角的概念,是立体几何计算题的证明要点。当用传统的演绎推理法求上述角时,必须详尽写明所作的辅助直线、辅助平面;必须按照空间角的定义进行证明。然后计算。然而,用解析法和向量法没有上述要求。
3. 空间的角包括平面几何的相交直线所成的角、平行直线所成的角。
1.空间角的定义体现了空间问题平面化的数学思想。把空间的角转化为相交直线(如异面直线所成角、直线与平面所成角)或两条射线(如二面角的平面角)所成角。
2.空间角的概念,是立体几何计算题的证明要点。当用传统的演绎推理法求上述角时,必须详尽写明所作的辅助直线、辅助平面;必须按照空间角的定义进行证明。然后计算。然而,用解析法和向量法没有上述要求。
3. 空间的角包括平面几何的相交直线所成的角、平行直线所成的角。
空间角度定义
当直线是平面的斜线(相交但不垂直)时,斜线与其在平面的射影的夹角,叫直线与平面所成的角。
规定:当直线在平面内或直线与平面平行时,直线与平面所成角为0°;当直线与平面垂直时,直线与平面所成角为90°.
空间角度范围
直线与平面所成角的范围是[0,π/2].
空间角度求法
(1)定义法
按照直线与平面所成角的定义。一般通过面的垂线,确定斜线射影。转化成斜线与射影的夹角。然后,解三角形求角。
(2)法向量法
1°转化成平面的法向量,与斜线的方向向量所成角的余角,或补角的余角。即用公式
sin<向量n,向量b>=|n·b|/|n||b|.
2°转化成斜线的方向向量, 与斜线射影方向向量所成角,或补角。即用公式
cos<向量a,向量a′>=(a·a′)/|a|| a′|.
- 相关百科
- 相关知识
- 相关专栏
- 空间解析几何与线性代数第2版
- 空间认知与抽象过程
- 空间认知能力
- 空间设计与配色色彩控
- 空间设计中的照明手法
- 空间设计基础
- 空间设计基础(第4版)
- 空间设计宝典1-办公风水宜忌
- 空间设计宝典2-商业风水宜忌
- 空间设计宝典3-风水吉祥物宜忌
- 空间设计宝典4-方位风水宜忌
- 空间设计实用手绘表达
- 空间设计师
- 空间设计技法图典
- 空间设计概论与设计方法
- 空间设计自己来
- 中国铁道建筑总公司地下空间安全管理知识培训
- 应用螺杆钻定向钻探技术在复杂地层施工空间型定向孔
- 基于PLC控制星三角启动存在问题及解决办法
- 构建对内联接通道发挥北承长江三角洲桥头堡作用
- 化油器三角针阀与阀座导致油耗高与溢油问题解决办法
- 国内外钢结构设计规范关于角焊缝限值及计算方法比较
- 冷拉圆钢、方钢、六角钢
- 建筑空间再生与高校文化传播以同济大学博物馆为例
- 克里姆特装饰元素在西安市东城区改造建筑空间中运用
- 基于PHOENICS罐顶环形空间防火防爆数值模拟
- 基于BIM技术大空间多重曲面蜂窝铝板吊顶施工方法
- 基于Revit二次开发空间网架结构BIM建模技术
- 建筑结构实体检测中关于结构空间尺寸检测及评定
- 柳工挺进长江三角洲扬州柳工建设机械有限公司成立
- 基于中国传统文化背景苏州私家园林角落空间形态营造
- 基于系统概念建筑结构地震破坏机制和破坏过程控制