抗混叠滤波器
抗混叠滤波器基本信息
| 中文名 | 抗混叠滤波器 | 外文名 | Anti aliasing filter |
|---|---|---|---|
| 类 型 | 低通滤波器 | 公 式 | XL·XC=K2 |
| 用 途 | 在输出电平中把混叠频率分量降低到微不足道的程度 | 关联滤波器 | 带通滤波器、带阻滤波器 |
抗混叠滤波器(英语:Anti-aliasing filter,缩写AAF)是一种放在信号采样器之前的滤波器,用来在一个重点波段上限制信号的带宽,以求大致或完全地满足采样定理。此定理表示,当在奈奎斯特频率之上的频率功率为零时,从其信号的采样可实现无模糊重建。现实中的抗混叠滤波器会在带宽与混叠之间取舍。可实现的抗混叠滤波器一般允许出现一些混叠,或者减弱一些靠近奈奎斯特极限的频内频率。因此,许多实用的系统采样会高出实际的需求,以保证所有的重点频率都可重建,这种实践的方式称为过采样。
抗混叠滤波器造价信息
滤波器,顾名思义,是对波进行过滤的器件。“波”是一个非常广泛的物理概念,在电子技术领域,“波”被狭义地局限于特指描述各种物理量的取值随时间起伏变化的过程。该过程通过各类传感器的作用,被转换为电压或电流的时间函数,称之为各种物理量的时间波形,或者称之为信号。因为自变量时间‘是连续取值的,所以称之为连续时间信号,又习惯地称之为模拟信号(Analog Signal)。随着数字式电子计算机(一般简称计算机)技术的产生和飞速发展,为了便于计算机对信号进行处理,产生了在抽样定理指导下将连续时间信号变换成离散时间信号的完整的理论和方法。也就是说,可以只用原模拟信号在一系列离散时间坐标点上的样本值表达原始信号而不丢失任何信息,波、波形、信号这些概念既然表达的是客观世界中各种物理量的变化,自然就是现代社会赖以生存的各种信息的载体。信息需要传播,靠的就是波形信号的传递。信号在它的产生、转换、传输的每一个环节都可能由于环境和干扰的存在而畸变,有时,甚至是在相当多的情况下,这种畸变还很严重,以致于信号及其所携带的信息被深深地埋在噪声当中了。
滤波,本质上是从被噪声畸变和污染了的信号中提取原始信号所携带的信息的过程。

抗混叠滤波器定义
动态信号测试分析系统中为什么要使用抗混滤波器呢?大家都知道"奈奎斯特采样定律", 在对模拟信号进行离散化时,采样频率f2至少应2倍于被分析的信号的最高频率f1,即: f2≥2 f1;否则可能出现因采样频率不够高,模拟信号中的高频信号折叠到低频段,出现虚假频率成分的现象(如下图所示),称之为:混叠。
抗混叠滤波器常见问题
-
从电气工程上,所有的元件可以归纳为三类最基本的元件,即电阻,电感和电容.电阻的阻值与交流电的频率无关.电感的阻值(称为感抗)Xl=2πfL,即与交流电的频率成正比.频率越高,感抗越大.电容元件则与电感...
-
这个必须接合图纸来说明较清楚些,简单地说吧就是利用电容,电感量的不一样,所对不同频率产生的阻抗不一样.阻抗大的被阻挡,阻抗小的被通过.同时也可以利用电容,电感对某个频段产生偕振,使之通过或被阻挡.这就...
-
模拟的一阶滤波器带外衰减是20db/十倍频,而二阶则是40db/十倍频,阶数越高带外衰减越快。可以粗略地认为阶数越高滤波效果越好,但有时可能需要折中考虑相移,稳定性等因素。
抗混叠滤波器基本原理
工程测量中采样频率不可能无限高也不需要无限高,因为一般只关心一定频率范围内的信号成份。为解决频率混叠,在对模拟信号进行离散化采集前,采用低通滤波器滤除高于1/2采样频率的频率成份。实际仪器设计中,这个低通滤波器的截止频率(fc) 为:
截止频率(fc)=采样频率(fs) / 2.56
在进行动态信号测试中测量仪器必须具有抗混滤波功能,例如:在大型桥梁、高楼、机械设备等动态振动测试及模态分析中,信号所包含的频率成份理论上是无穷的。例如:桥梁的模态理论上有无限多个,但我们只关心对振动贡献最大的前几阶模态。如果不对振动的模拟信号进行低通抗混滤波,高阶模态频率很可能会混叠到低频段,形成虚假的模态频率,给模态参数识别带来困难。
抗混叠滤波器性能指标
抗混滤波器一般指低通滤波器,但滤波器有低通滤波器、带通滤波器、带阻滤波器、高通滤波器、高阻滤波器。滤波器的主要性能指标以低通滤波器为例,理想的低通滤波器为矩形,但实际中是不可能实现的。衡量低通滤波器性能的指标主要包括以下几方面:
带内波纹度:通带的幅值精度指标,例如:带内波纹度为±0.1dB时,对幅值精度的影响约为±1%(这正是为什么一般的数采器幅值精度可以做到千分之几,一般的数采器用很高的采样频率进行采集,不加低通滤波器)。
阻带下降斜率:滤波器在截至频率开始下降,下降斜率越大越好。一般采用每个倍频程的下降分贝数衡量,例如:满足工程测量需要的阻带下降斜率约为-80dB/oct。
滤波器落差:带通到带阻差值的分贝数dB。
值得一提的是:随着DSP信号处理芯片的出现,现代测试仪器中已采用模拟滤波加数字滤波,使滤波器性能指标突飞猛进。例如:带内波纹度可达±0.05dB,阻带下降斜率可达到约-200dB/oct,大大好于纯模拟滤波器。
巴特沃斯响应(最平坦响应)
巴特沃斯响应能够最大化滤波器的通带平坦度。该响应非常平坦,非常接近DC信号,然后慢慢衰减至截止频率点为-3dB,最终逼近-20ndB/decade的衰减率,其中n为滤波器的阶数。巴特沃斯滤波器特别适用于低频应用,其对于维护增益的平坦性来说非常重要。
贝塞尔响应
除了会改变依赖于频率的输入信号的幅度外,滤波器还会为其引入了一个延迟。延迟使得基于频率的相移产生非正弦信号失真。就像巴特沃斯响应利用通带最大化了幅度的平坦度一样,贝塞尔响应最小化了通带的相位非线性。
切贝雪夫响应
在一些应用当中,最为重要的因素是滤波器截断不必要信号的速度。如果你可以接受通带具有一些纹波,就可以得到比巴特沃斯滤波器更快速的衰减。附录A包含了设计多达8阶的具巴特沃斯、贝塞尔和切贝雪夫响应滤波器所需参数的表格。其中两个表格用于切贝雪夫响应∶一个用于0.1dB最大通带纹波;另一个用于1dB最大通带纹波。
板上滤波器虽然对高频的滤波效果不理想,但是如果应用得当,可以满足大部分民用产品电磁兼容的要求。在使用时要注意以下事项:
抗混叠滤波器干净地
如果决定使用板上滤波器,在布线时就要注意在电缆端口处留出一块“干净地”,滤波器和连接器都安装在“干净地”上。通过前面的讨论,可知信号地线上的干扰是十分严重的。如果直接将电缆的滤波电容连接到这种地线上,会造成严重的共模辐射问题。为了取得较好的滤波效果,必须准备一块干净地。并与信号地只能在一点连接起来,这个流通点称为“桥”,所有信号线都从桥上通过,以减小信号环路面积。
抗混叠滤波器并排设置
同一组电缆内的所有导线的未滤波部分在—起,已滤波部分在一起。否则,一根导线的未滤波部分会将另一根导线的已滤波部分重新污染使电缆整体滤波失效。
抗混叠滤波器靠近电缆端口
滤波器与面板之间的导线的距离应尽量短。必要时,使用金属板遮挡一下,隔离近场干扰。
抗混叠滤波器与机箱的搭接
安装滤波器的干净地要与金属机箱可靠地搭接起来,如果机箱不是金属的,就在线路板下方设置一块较大的金属板来作为滤波地。干净地与金属机箱之间的搭接要保证很低的射频阻抗。如有必要,可以使用电磁密封衬垫搭接,增加搭接面积,减小射频阻抗。
抗混叠滤波器接地线要短
考虑到引脚的电感效应,其重要性前面已讨沦,滤波器的局部布线和设计线路板与机箱(金属板)的连接结构时要特别注意。
抗混叠滤波器分组
在端口滤波的电缆和不滤波的电缆应尽量远离,防止发生上述的耦合问题。 2100433B
抗混叠滤波器文献

 超宽带声表面波滤波器的设计
超宽带声表面波滤波器的设计
该文精确模拟了基于弛豫铁电单晶的声表面波(SAW)梯形滤波器的性能。首先介绍了由谐振器构成的梯形SAW滤波器的工作原理,利用QUCS软件建立了七阶梯形滤波器的仿真模型。结果表明,该单晶能实现高达620 MHz的超宽带SAW滤波器(中心频率1GHz),比传统压电材料的滤波器带宽高3倍;通过优化各支路谐振器的静态电容及传统梯型滤波器的结构,牺牲了一定的带宽,但获得了较高的带外抑制和过渡带的陡峭度;讨论了不同品质因数对滤波器带内插损的影响。
在有些情况下,人们希望采样频率超出信号带宽的两倍这样就可以用数字滤波器替换性能不好的模拟抗混叠滤波器,这个过程称为过采样。
这篇内容我们说说电表配置,不多说,就说说通用系统中最常用的单相和三相配置。ps.有关抗混叠滤波器、衰减网络或其他任何需要进行特定IC设计的保护电路详情,可参考特定产品的评估板用户指南。
单相配置
这是最基本的单相连接配置。它仅有两条导线:相位和零线。图1显示阻性分流器用作电流传感器。该配置也可使用其他任何电流传感器。

图1. 单相、单个电流传感器
图2为防窃电连接示意图,使用电流互感器(CT)进行防窃电检测。通常,在这些情况下必须至少使用一个CT或罗氏线圈作为传感器,起到隔离作用。

图2. 单相、两个电流传感器
在某些单相应用中,可能需要测量两个负载的功率,从而检测两路电流信号。这类应用称为裂相应用,可在这类裂相配置中使用ADE IC。如需获得总功率,可使用任意单相ADE IC,然后根据图3中的配置进行设置。
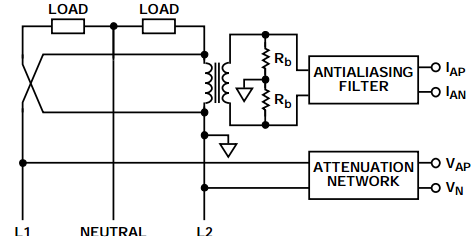
图3. 裂相、单个电流传感器
可使用单个电流互感器作为电流传感器,并采用相反方向连接的两条线路作为输入。线路L1和L2的电压差输入衰减网络。
如需测量单个负载功率,可使用带有零线通道的单相ADEIC。理想情况下,零线通道测量的目的是检测窃电条件,但零线通道与其他内部电流通道完全一样,因此IC可视为具有两条相等的电流通道。电表可按图4所示进行连接,实现该功能。然而,只有假定两条线路的电压完全相等时才能这么做。因此,将零线和其中一条线路的电压差输入衰减网络。
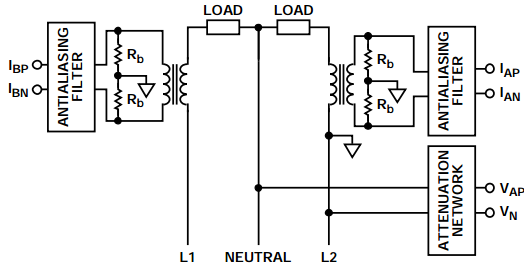
图4. 裂相、两个电流传感器
三相配置
图5显示配备了3个电压传感器的四线式Y型配置。该配置使用了3个电压传感器,分别对应三个相位。由于三个相位的电流和电压均可测得,因此计算功率非常简单。该配置是所有ADE IC中的默认配置。
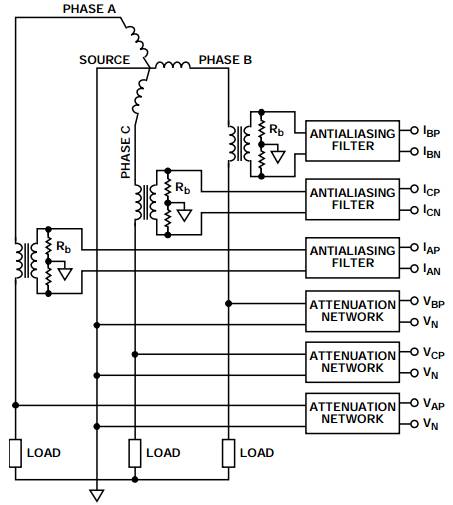
图5. 配备3个电压传感器的四线式Y型配置
有功功率 = VA × IA +VB × IB + VC × IC
= (VAP – VN) × (IAP – IAN) + (VBP – VN) × (IBP – IBN) + (VCP – VN) × (ICP – ICN)
还可根据同样的逻辑,说明该配置下累加无功功率和视在功率的计算。
图6显示配备了两个电压传感器的四线式Y型配置。该配置相比上一个配置有所不同,因为它不测量其中一个相位的电压。

图6. 配备两个电压传感器的四线式Y型配置
由图6可见,相位B的电压不予测量,但可通过获得的其他数值计算功率。
理想情况下,VA + VB + VC = 0。因此,假设VB = −VA − VC。
有功功率 = VA × IA +VB × IB + VC × IC
= VA × IA + (-VA – VC) × IB + VC × IC
= VA × (IA – IB) + VC × (IC – IB)
= (VAP – VN) × ((IAP – IAN) − (IBP – IBN)) + (VCP – VN) × ((ICP – ICN) − (IBP – IBN))
根据相同的逻辑,三相ADE IC的无功功率累加计算可证明是正确的。对于某些产品,如本文所述,可在相关寄存器内通过相位A和相位C的电压计算相位B的电压,从而计算出正确的视在功率。但是,这种计算的前提是系统对称且平衡。
图7显示三线式三角形配置。该三角形配置以其中一个相位作为参考,通过其他相位并参照该相位完成测量。在大部分较新的IC中,强制选择相位B作为参考。

图7. 三线式三角形配置
由于闭环,IA + IB + IC = 0。因此,假设IB = −IA − IC
有功功率 = VA x IA +VB x IB + VC x IC = VA x IA +VB x (-IA – IC) + VC x IC = (VA – VB) × IA+ (VC – VB) × IC
由于相位B用作参考,VA等于VAB,VC等于VCB
= (VAP – VN) × (IAP – IAN) + (VCP – VN) × (ICP – ICN)
类似地,在该配置中,三相ADE IC产生的累加无功功率也可证明是正确的。但是,视在功率的计算结果可能是错误的,因为在该配置下芯片会将线路间电压当作相电压。某些IC可能会将相位B计算为相位A和相位C的电压差,并假设系统是平衡的。另外,如上所述,还需考虑相位B的功耗。等效Y型配置的视在功率可通过将得到的结果除以√3计算得出。
图8显示四线式三角形配置。该配置是三角形配置,它测量所有三个相位的电流。该配置还存在一个独立的零线端子。此外,不测量相位B的电压。由于零线位于相位A和相位B之间,因此将其视为与相位A幅度相等但符号相反。

图8. 四线式三角形配置
因此,假设VB = −VA
有功功率 = VA × IA +VB × IB + VC × IC
= VA × IA - VA × IB + VC × IC
= VA × (IA – IB) + VC × IC
= (VAP – VN) × ((IAP – IAN) − (IBP – IBN)) + (VCP – VN) × (ICP – ICN)
类似地,在该配置中,三相ADE IC产生的累加无功功率也可证明是正确的。但是,视在功率的计算结果可能是错误的,因为在该配置下IC会将线路间电压当作相电压。某些IC假定相位B电压的幅度与相位A电压幅度相等而符号相反,从而假定系统是对称且平衡的。等效Y型配置的视在功率可通过将得到的结果除以√3/2(相位A和相位B),以及除以3/2(相位C)计算得出。如果希望重新配置电表,将其从一种配置改变为另外一种,同时希望得到精确的结果,那么需要针对新设置重新校准ADE IC。
这几种最常用的单相和三相电表的配置方法你都get到了吗?
好文章 必须分享!
恒流源信号调理器的概述:北京声振研究所研制的SZTL-ICP恒流源信号调理器采用模块化设计(1~256通道自行组合) 、内置恒流源(ICP)、抗混叠滤波器、程控放大器、自调零、提供交流/直流耦合方式,直接接各种模拟输出传感器(一次仪表),如加速度计、传声器、力传感器、应变片、压力计、位移计等,能满足各种高精度动态信号测试分析的要求。
- 相关百科
- 相关知识
- 相关专栏
- 永固紫RL
- 自适应滤波器
- 火灾警报器
- WX-B·APF 矿用隔爆型有源电力滤波器
- 共模滤波器
- 一阶低通滤波器
- 嵌入式InternetTCP·IP基础
- 交流滤波器
- 嵌入式系统中的模拟设计
- 光学低通光波滤波器
- 信号滤波器
- 谐波滤波器
- 嵌入式系统原理与实践:ARM Cortex-M4 Kinetis微控制器
- EMC滤波器
- 嵌入式系统设计及应用
- 贝塞尔滤波器
- 增设钢牛腿在连续独柱墩桥梁抗倾覆加固设计中的应用
- 张峰水库2号倒虹预应力钢筒混凝土管道安装施工工艺
- 中国建筑抗震设计规范的演变与展望
- 异形柱框架及短肢墙抗震节点构造的施工质量保证措施
- 中、小跨径钢筋混凝土拱桥现浇支架(拱架)设计指南
- 圆形截面钢筋混凝土受弯构件正截面承载力的简化计算
- 整体平移后六层砖混结构住宅楼整体提升的施工与监测
- 圆CFRP-钢管混凝土轴压短柱荷载-变形关系分析
- 在建工程评审制度在预拌混凝土生产计划管理中的应用
- 中国预应力混凝土管桩的发展状况及同日本管桩的差距
- 正交法在沙坪水电站工程泵送混凝土配合比设计的应用
- 植被混凝土在水利边坡工程中进展和应用现状
- 在小桥涵软基处理中如何运用预应力混凝土管桩的分析
- 无收缩预应力混凝土高性能灌浆材料与应用
- 宜兴抽水蓄能电站地下厂房岩壁梁混凝土温控防裂技术
- 增效剂在水工高性能混凝土中增效机理及其应用


