卡尔曼滤波器应用实例
卡尔曼滤波的一个典型实例是从一组有限的,包含噪声的,对物体位置的观察序列(可能有偏差)预测出物体的位置的坐标及速度。在很多工程应用(如雷达、计算机视觉)中都可以找到它的身影。同时,卡尔曼滤波也是控制理论以及控制系统工程中的一个重要课题。
例如,对于雷达来说,人们感兴趣的是其能够跟踪目标。但目标的位置、速度、加速度的测量值往往在任何时候都有噪声。卡尔曼滤波利用目标的动态信息,设法去掉噪声的影响,得到一个关于目标位置的好的估计。这个估计可以是对当前目标位置的估计(滤波),也可以是对于将来位置的估计(预测),也可以是对过去位置的估计(插值或平滑)。
目标跟踪示例代码:(具体解释请见参考资料 )
Z=(1:100); %观测值
noise=randn(1,100); %方差为1的高斯噪声
Z=Z+noise;
X=[0;0]; %状态
P=[1 0;0 1]; %状态协方差矩阵
F=[1 1;0 1]; %状态转移矩阵
Q=[0.0001,0;0,0.0001]; %状态转移协方差矩阵
H=[1 0]; %观测矩阵
R=1; %观测噪声方差
figure;
hold on;
for i=1:100
X_ = F*X;
P_ = F*P*F'+Q;
K = P_*H'/(H*P_*H'+R);
X = X_+K*(Z(i)-H*X_);
P = (eye(2)-K*H)*P_;
plot(X(1), X(2)); %画点,横轴表示位置,纵轴表示速度
end
卡尔曼滤波器造价信息
在这一部分,我们就来描述源于Dr Kalman 的卡尔曼滤波器。下面的描述,会涉及一些基本的概念知识,包括概率(Probability),随机变量(Random Variable),高斯或正态分配(Gaussian Distribution)还有State-space Model等等。但对于卡尔曼滤波器的详细证明,这里不能一一描述。
首先,我们先要引入一个离散控制过程的系统。该系统可用一个线性随机微分方程(Linear Stochastic Difference equation)来描述:
X(k)=A X(k-1)+B U(k)+W(k)
再加上系统的测量值:
Z(k)=H X(k)+V(k)
上两式子中,X(k)是k时刻的系统状态,U(k)是k时刻对系统的控制量。A和B是系统参数,对于多模型系统,他们为矩阵。Z(k)是k时刻的测量值,H是测量系统的参数,对于多测量系统,H为矩阵。W(k)和V(k)分别表示过程和测量的噪声。他们被假设成高斯白噪声(White Gaussian Noise),他们的covariance 分别是Q,R(这里我们假设他们不随系统状态变化而变化)。
对于满足上面的条件(线性随机微分系统,过程和测量都是高斯白噪声),卡尔曼滤波器是最优的信息处理器。下面我们来用他们结合他们的covariances 来估算系统的最优化输出(类似上一节那个温度的例子)。
首先我们要利用系统的过程模型,来预测下一状态的系统。假设现在的系统状态是k,根据系统的模型,可以基于系统的上一状态而预测出现在状态:
X(k|k-1)=A X(k-1|k-1)+B U(k) ……….. (1)
式(1)中,X(k|k-1)是利用上一状态预测的结果,X(k-1|k-1)是上一状态最优的结果,U(k)为现在状态的控制量,如果没有控制量,它可以为0。
到现在为止,我们的系统结果已经更新了,可是,对应于X(k|k-1)的covariance还没更新。我们用P表示covariance:
P(k|k-1)=A P(k-1|k-1) A'+Q ……… (2)
式(2)中,P(k|k-1)是X(k|k-1)对应的covariance,P(k-1|k-1)是X(k-1|k-1)对应的covariance,A'表示A的转置矩阵,Q是系统过程的covariance。式子1,2就是卡尔曼滤波器5个公式当中的前两个,也就是对系统的预测。
现在我们有了现在状态的预测结果,然后我们再收集现在状态的测量值。结合预测值和测量值,我们可以得到现在状态(k)的最优化估算值X(k|k):
X(k|k)= X(k|k-1)+Kg(k) (Z(k)-H X(k|k-1)) ……… (3)
其中Kg为卡尔曼增益(Kalman Gain):
Kg(k)= P(k|k-1) H' / (H P(k|k-1) H' + R) ……… (4)
到现在为止,我们已经得到了k状态下最优的估算值X(k|k)。但是为了要令卡尔曼滤波器不断的运行下去直到系统过程结束,我们还要更新k状态下X(k|k)的covariance:
P(k|k)=(I-Kg(k) H)P(k|k-1) ……… (5)
其中I 为1的矩阵,对于单模型单测量,I=1。当系统进入k+1状态时,P(k|k)就是式子(2)的P(k-1|k-1)。这样,算法就可以自回归的运算下去。
卡尔曼滤波器的原理基本描述了,式子1,2,3,4和5就是他的5 个基本公式。根据这5个公式,可以很容易的实现计算机的程序。
为了可以更加容易地理解卡尔曼滤波器,这里会应用形象的描述方法来讲解,而不是像大多数参考书那样罗列一大堆的数学公式和数学符号。但是,他的5条公式是其核心内容。结合现代的计算机,其实卡尔曼的程序相当的简单,只要你理解了他的那5条公式。
在介绍他的5条公式之前,先让我们来根据下面的例子一步一步的探索。
假设我们要研究的对象是一个房间的温度。根据你的经验判断,这个房间的温度是恒定的,也就是下一分钟的温度等于现在这一分钟的温度(假设我们用一分钟来做时间单位)。假设你对你的经验不是100%的相信,可能会有上下偏差几度。我们把这些偏差看成是高斯白噪声(White Gaussian Noise),也就是这些偏差跟前后时间是没有关系的而且符合高斯分布(Gaussian Distribution)。另外,我们在房间里放一个温度计,但是这个温度计也不准确的,测量值会比实际值偏差。我们也把这些偏差看成是高斯白噪声。
好了,现在对于某一分钟我们有两个有关于该房间的温度值:你根据经验的预测值(系统的预测值)和温度计的值(测量值)。下面我们要用这两个值结合他们各自的噪声来估算出房间的实际温度值。
假如我们要估算k时刻的是实际温度值。首先你要根据k-1时刻的温度值,来预测k时刻的温度。因为你相信温度是恒定的,所以你会得到k时刻的温度预测值是跟k-1时刻一样的,假设是23度,同时该值的高斯噪声的偏差是5度(5是这样得到的:如果k-1时刻估算出的最优温度值的偏差是3,你对自己预测的不确定度是4度,他们平方相加再开方,就是5)。然后,你从温度计那里得到了k时刻的温度值,假设是25度,同时该值的偏差是4度。
由于我们用于估算k时刻的实际温度有两个温度值,分别是23度和25度。究竟实际温度是多少呢?相信自己还是相信温度计呢?究竟相信谁多一点,我们可以用他们的covariance来判断。因为Kg^2=5^2/(5^2+4^2),所以Kg=0.78,我们可以估算出k时刻的实际温度值是:23+0.78*(25-23)=24.56度。可以看出,因为温度计的covariance比较小(比较相信温度计),所以估算出的最优温度值偏向温度计的值。
现在我们已经得到k时刻的最优温度值了,下一步就是要进入k+1时刻,进行新的最优估算。到现在为止,好像还没看到什么自回归的东西出现。对了,在进入k+1时刻之前,我们还要算出k时刻那个最优值(24.56度)的偏差。算法如下:((1-Kg)*5^2)^0.5=2.35。这里的5就是上面的k时刻你预测的那个23度温度值的偏差,得出的2.35就是进入k+1时刻以后k时刻估算出的最优温度值的偏差(对应于上面的3)。
就是这样,卡尔曼滤波器就不断的把covariance递归,从而估算出最优的温度值。他运行的很快,而且它只保留了上一时刻的covariance。上面的Kg,就是卡尔曼增益(Kalman Gain)。他可以随不同的时刻而改变他自己的值,是不是很神奇!
下面就要言归正传,讨论真正工程系统上的卡尔曼。
卡尔曼滤波器应用实例常见问题
-
卡尔曼滤波(Kalman filtering)一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过...
-
在cnki上下篇kalman目标跟踪的硕士论文吧,很多的,当然期刊也可以,不过一般情况下硕士论文讲的能详细点,然后找准一篇仔细研读,这样子基本上理论就没啥问题了,编程就用MATLAB,用C很麻烦,很多...
-
EKF是对非线性系统模型(方程)进行的线性化近似,以利用KF算法进行滤波估计。而UKF是对状态的概率统计近似,即设计少量的σ点,由σ点经由非线性函数的传播,计算出随机向量一、二阶统计特性的传播,对于高...
卡尔曼滤波器应用实例文献

 基于卡尔曼滤波器的传像光纤束位置搜索
基于卡尔曼滤波器的传像光纤束位置搜索
为获取超高分辨率图像,设计了一种入端为线阵排列、出端为面阵排列的传像光纤束.利用该光纤束的成像系统在合成目标图像时,需要建立光纤束出端、入端位置坐标表.介绍了一种基于卡尔曼滤波器的算法,对出端光纤位置逐一搜索;搜索光纤位置时区分层内、层间设置不同初始步长,按均方误差最小原则对搜索步长进行修正.算法采用了比对终止边界、标定已搜索光纤两种稳健性措施,‘Z’字型搜索路径提高了算法效率.实验结果表明,搜索算法得到的位置坐标表准确标定光纤位置,提取光纤束耦合的信息还原了目标图像.

 自适应卡尔曼滤波在建筑物变形监测中的应用
自适应卡尔曼滤波在建筑物变形监测中的应用
本文参考有关文献并结合西安高新区SOHU同盟北楼D7点沉降量观测数据分析实例。以卡尔曼滤波的4个特点(见本文末)。介绍了自适应卡尔曼滤波系统在建筑物变形监测的预测预报方面的应用及其优越性。

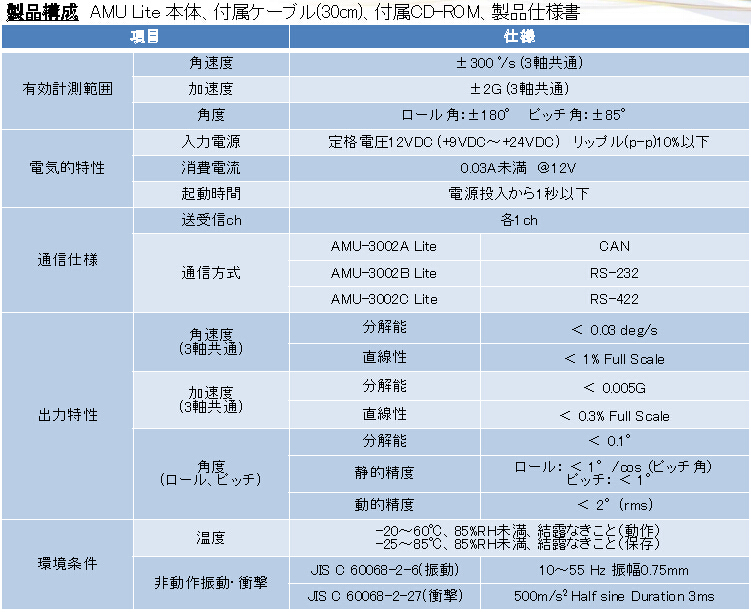
AMU-Lite惯性测量单元
3轴陀螺传感器和加速度传感器
它是一种紧凑的姿态角度检测器/惯性测量装置,可以在动态环境下并入并输出横滚角和俯仰角。
每个传感器的温度特性和卡尔曼滤波器校正,可以高精度地获取姿态信息和惯性测量信息。
特点:
紧凑轻便
尺寸:53×32×19.5毫米重量:小于40克
角度测量
动态环境下稳定的俯仰角, 横滚角测量。
通讯方式
从3种类型的CAN,RS232,RS422中选择。
准备多个输出周期,并在系统中可以组合选择。
演示软件
根据演示软件(包括主机),角度,角速度,
加速度的测量数据可以由PC取出。
应用领域:
* 船舶运动测量,姿态测量
* 汽车和摩托车的位置测量
* 机器人姿态控制
* 农机自主旅游
* UAV,水下机器人姿态控制
* 施工机械定向测量
传统的柱上高压真空断路器测量方法只在一定的真空度范围内测量精度较高,且易受外界干扰,为了获得准确的真空度数据,使用横磁场脉冲磁控法和改进的屏蔽罩电位法测量真空度,利用联合卡尔曼滤波器对测量数据进行融合。根据真空灭弧室的离线检测方式和真空度变化的规律确定了联合卡尔曼滤波的初始值和系数矩阵。实验证明这种方法具有良好的容错性,能够有效抑制外部噪声对测量系统的干扰,提高测量数据的稳定性和准确度。
随着我国电力系统无油化改造的顺利实施和电力设备制造技术的飞速发展,真空断路器的使用日趋普及。真空断路器具有体积小、重量轻,环境污染小;开端容量大,灭弧性能好;适合频繁操作,可靠性高,电寿命长等优点。在6~35kV电压等级断路器中占有主导地位,还正在向高电压(72.5kV以上)、低电压(380V~3kV)两极发展。真空断路器是以真空作为绝缘和灭弧手段的断路器,真空度直接影响断路器的性能。目前较为实用的真空度测量方法是横磁场脉冲磁控法和改进的屏蔽罩电位法,实行离线检测,即不必测量正在工作的真空

断路器的真空度,只需在定期检修时测量。但这两种测量方法只在一定的真空度范围内测量精度较高,脉冲磁控放电法能够测量的灭弧室真空度的量程范围为10-1~10-4 Pa,而屏蔽罩电位法只有在真空度处于10-1~1Pa时测量更精确。同时由于真空断路器所处的磁场、电场环境比较恶劣,单一传感器可能会因为故障或干扰导致测量不准确。若采用多个传感器,通过数据融合的方法把不同种类的传感器所提供的观测量加以综合,可以消除多个传感器之间可能存在的矛盾,降低不确定性,从而获得真空度准确的状态估计,提高设备状态检测系统故障的准确性。
常用的数据级的数据融合方法有基于均值的递推融合算法、小波分析法、卡尔曼滤波器法等。卡尔曼滤波器采用最优化递归处理算法,能根据测量结果实时自动调整滤波器系数,提高融合精度。但传统卡尔曼滤波数据融合有其不足的地方,当其中一个传感器出现故障造成数据信息错误时,对最终数据融合结果影响较大,也就是系统的鲁棒性较差。联合卡尔曼滤波弥补了上述不足,采用信息分配原理,能及时有效地检测传感器的故障,进一步提高系统的总体性能。
本文以联合卡尔曼滤波算法为基础,得到了多个传感器的最优融合数据,该方法可以获得比传统的单独一种真空度测量方法更有效、更可靠的数据,提高了真空度检测的精度。
1、原理与模型的建立

联合卡尔曼滤波是一种特殊的分散式卡尔曼滤波器,分为局部滤波器和主滤波器两部分。每个传感器的测量值只提供给对应的局部滤波器,各局部滤波器并行处理,获得建立在局部测量基础上的局部最优估计。这些局部最优估计值又在主滤波器中进行进一步的融合处理,从而获得建立在所有测量值基础上的全局最优估计。然后主滤波器根据信息分配权值对局部滤波器进行反馈重置,提高局部滤波器的精度。本文采用横磁场脉冲磁控法和屏蔽罩电位法测得真空灭弧室的真空度,之后由DSPF2812对信号进行采集和融合处理。联合卡尔曼滤波器的结构如图1所示。
联合卡尔曼滤波器的结构
图1 联合卡尔曼滤波器的结构

端口ADCINB0的数据在[1.450,1.900]的范围内波动,在第2500Ls左右,测量数据出现异常波动。该组数据平均值为1.663V,方差为0.0380。测量数据无收敛趋势,受外界因素的影响较大。该组数据为卡尔曼滤波器处理后的电压值,在实验开始阶段数据波动较大,甚至超过单传感器测量数据的[1.450,1.900]的范围,但随着实验的继续进行,数据的收敛趋势明显,而且在2500Ls左右有效地抑制了数据的异常波动。处理后的数据平均值为1.657V,方差为0.0048,相对于未经处理的数据,降低了一个数量级。
考虑到真空度测量时的测量噪声、状态噪声无法准确获得,采用的是合理假设后的估计值,使得最终的融合数据仍有一定幅度的波动。总的来说卡尔曼滤波器数据融合方法能有效地提高数据的一致性,降低外界环境的变化对测量结果的影响。
4、结论
本文针对单独一种测量方法测量灭弧室真空度不准确的问题,提出了采用两种不同方法测量,并使用基于联合卡尔曼滤波器的数据融合方法,对测量数据进行处理。仿真实验表明该方法的有效性,能够有效解决单独一种传感器测量真空度不准确的问题。
针对动力定位水面船舶,基于Luenberger观测器构造原理及Lyapunov稳定性理论,构造一个船舶动力定位系统的非线性状态观测器。设计观测器较卡尔曼滤波器的主要优越性在于不需要对船舶的运动方程进行线性化处理,且具有全局的指数稳定性。最后,用一艘供给船对所设计观测器进行数值仿真研究,仿真结果表明所设计非线性观测器具有良好的滤波及状态估计性能,船舶运动状态估计值指数收敛于其实际值,验证了所设计船舶动力定位系统非线性观测器的有效性。 2100433B
- 相关百科
- 相关知识
- 相关专栏
- 盛达BIPAC-2AB
- 通信系统微波滤波器
- fclub
- 晶闸管控制电抗器
- 共模电感
- NS4263
- 五峰百利建业
- DSP-206多功能数字音频处理器
- 911聚氨酯防水涂料
- 无线电技术基础
- 传感器调理电路设计理论及应用
- 聚合
- DSP技术与应用实例(第2版)
- 压差流量计
- 离散时间信号处理
- 高能离子空气净化系统
- 分形DGS单元结构设计及其在微带电路中的应用
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 云计算技术在城市轨道交通运营指挥管理系统中的应用
- 应对水源突发污染的城市供水应急处理技术与应用
- 有限元法在软土浅埋隧道施工过程的动态模拟中的应用
- 新型基于热力学法的水泵效率数学模型及应用
- 振冲碎石桩地基加固技术在椒江标准海塘工程中的应用
- 应用亚温淬火工艺解决45钢槽型螺母淬裂问题的探索
- 乙烯基树脂混凝土电解槽的性能及在湿法冶金中的应用
- 应用清单招标与经评审的最低投标价法评标的几点思考
- 智能化技术在电气工程自动化控制中的应用与实践研讨
- 应用型人才培养模式下高校机电工程综合实践改革探索
- 智能电力监控管理系统在某飞机维修公司工程中的应用
- 异形人工挖孔桩和预应力土层锚杆组合在基坑中的应用
- 智能照明系统在高校教学楼建筑节能改造中的应用
- 圆形截面预应力钢筋混凝土悬臂式支护桩的分析与应用