建筑给水排水水力学的图算法
建筑给水排水水力学的图算法基本信息
| 书 名 | 建筑给水排水水力学的图算法 | 作 者 | 周进 |
|---|---|---|---|
| ISBN | 9787112076857 | 出版社 | 中国建筑工业出版社 [2] |
| 出版时间 | 2005-10-15 | 装 帧 | 平装 |
图书目录
Chapter1 GeneralChapter2 Definitions and notationsChapter3 Basic requirements of seismic designChapter4 Site,Subsoil and FoundationChapter5 Seismic action and seismic checking for structures;Chapter6 Multi-story and tall reinforced building;Chapter7 M2100433B
建筑给水排水水力学的图算法造价信息
建筑给水排水水力学的图算法常见问题
-
这个问题比较复杂,我是给水排水工程的新生,还不是太了解,你还是自己看吧! 参考资料: http://www.gpszy.com/?action-viewthread-tid-537
-
你指的是材料还是,专业啊。
-
1.1依附于土木工程,尚未独立设置专业阶段(1952年以前)在中华人民共和国成立前及成立初期,在高等教育中没有独立设置给水排水工程专业,有关的基本教学内容设在土木工程专业之中或作为土木工程专业的一个专...
建筑给水排水水力学的图算法文献

 建筑给水排水
建筑给水排水
1 / 6 给排水安装工艺标准 1.材料设备管理 (1)建筑给水、排水及采暖工程使用的管材、配件、卫生器具、散热器等,必 须具有质量合格证明文件, 规格、型号及性能检测报告应符合国家技术标准或设 计要求。进场时必须经专职质检员验收,并经监理工程师核查确认,方可使用。 (2)所有材料进厂时,应对品种、规格、外观等进行验收。包装应完好,表面 无划痕及外力冲击破损。 (3)阀门安装前,应作强度和严密性试验。试验应在每批(同牌号、同型号、 同规格)数量中抽查 10%,且不少于一个。 对于安装在主干管上起切断作用的闭 路阀门,应逐个作强度和严密性试验。 s 2.施工过程质量控制 (1)建筑给水、排水及采暖工程施工时应和土建搞好配合,作好洞口和预埋管 件的预留工作,应进行交接质量检验并形成记录。 (2)隐蔽工程应在隐蔽前经专职质检员验收合格后,必须经监理工程师验收并 办理隐蔽工程签证,方能隐蔽,并

 第3章-给水排水管网水力学基础
第3章-给水排水管网水力学基础
第3章-给水排水管网水力学基础
《土木工程图算法》用图算法简化了土木工程中的建筑、给排水、水力学、路桥等专业书籍的几十种计算,详述了算图绘制方法,其中三种高次方程图算法具有通用性。《土木工程图算法》内容简洁易懂,可与参考文献对照,适合土木工程技术人员和师生参考。附录6计算人的体重指数图算法易被广大读者所运用。
本书由DanaiKoutra和全球知名的数据挖掘领域奠基人之一ChristosFaloutsos教授合著,介绍了图挖掘领域一个崭新的研究方向。全书内容主要包括两个部分:第壹部分介绍了单图上的概要表示以及节点标签分类算法;第二部分介绍了群图上的概要表示以及群图的相似性度量和节点对齐算法。

鉴于图割方法的明显优势,白雪冰及其团队采用Graph Cuts算法和Grab Cut算法分别对木材表面的单目标和多目标缺陷图像进行分割试验,以总结传统图割方法的不足和改进算法的优点。
针对传统Graph Cuts算法只能针对灰度图像进行分割、运行时参数的选择比较复杂,并且存在该算法效率和精度较低的缺陷,采用这两种方法分别对3种木材表面缺陷活节、虫眼和死节图像进行分割实验。为了验证Grab Cuts方法的适用性,用含有多个缺陷目标的木质板材图像做了图像分割验证。
结果表明:缺陷图像的目标和背景的种子点选取直接影响Graph Cuts算法的分割结果,Graph Cuts算法的计算效率较低,分割时间较长,对相邻像素间的区分度较差,分割结果不理想。改进后的Grab Cut算法是迭代的Graph Cuts,该方法虽然在图像分割前也需要人工画定初始化矩形框,但操作相对简单,分割结果能够得到完整的闭合缺陷区域边界,且不受木材表面缺陷的类型、数量、尺寸和缺陷形状的影响,分割效果好,分割速度快,抗噪性强,对灰度图像和彩色图像都可使用。
图割算法
1.1 Graph Cuts 算法的原理
图割(Graph Cuts)交互式图像分割算法是一种基于图论的组合最优化方法,其基础是最大流算法,将图像分割问题转化成能量函数的最小化问题,通过最小化能量函数,从而实现图像的最优分割。首先,建立能量函数:
E(L) = R(L) + λB(L) (1)
式中:R(L)是区域项,表示区域属性;B(L)是边界项,表示边界属性;λ 为平衡因子,当λ 较小时,边界项可忽略,当λ 较大时,图像的所有点被赋予相同标记。
设P={p1,p22,…,pN2 } 是像素集合,L={0,1}是像素标记集合,0表示背景,1表示目标;像素的标记可以表示为从P到L的映射, 记作fp={fp| fp ∈L}。
因此,式(1)中的区域项表示为R(f)=Rp(fp ),p ∈ P,用Rp(fp) 来进行判定像素p分配给某种标记的可能性。通常对能量函数中的区域项取概率的负对数,且将预定义的种子点作为目标和背景的采样,以此估计目标和背景的灰度直方图分布,对于目标/背景的二值分割,区域项可表示为:
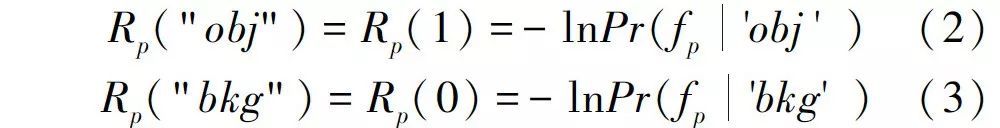
式(2)代表了像素p分配给目标区域的可能性,式(3)代表像素p分配给背景区域的可能性,随着可能性的增大, Rp(•) 的值会减小,从而可通过最小化能量函数来实现对图像的准确分割。式(1)的边界项可表示为:
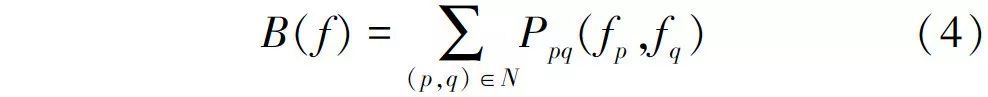
式中: p和q为相邻像素,边界项体现图像边界像素值的不连续性; N为4邻域或8邻域系统。通过变分模型可以将式(4)写为:
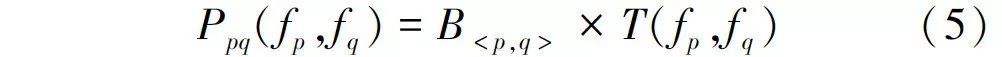
其中, T(fp ,fq ) 为指标函数,满足 :
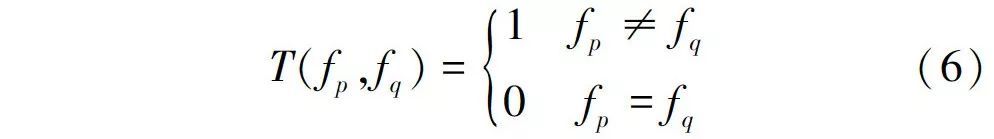
B < p,q > 为对像素p 、q不连续性的惩罚值:
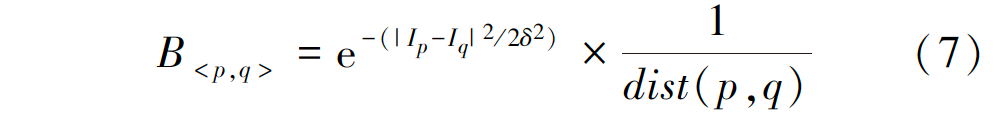
式中:Ip 、Iq为像素p、q的灰度值; dist(p,q)是p和q的距离; δ为图像噪声。p和q越相近,则B < p,q >越大;若p和q相差较大,则B < p,q >趋近于0 。当B < p,q >的值较小时,两个像素会更易于分给不同的区域,这时图像分割得到最小的能量值。
Graph Cuts算法源于图论,通过最小化能量函数实现图像分割 。首先要对(1)的能量函数公式来构造网络图,把表示带有非负边权的无向图G= (V,E)作为图像,其中V为顶点集,与其相对应图像的边集为像素点集P,E。V含有两个特殊的顶点,其一称为源节点S(代表目标),其二称为汇节点T(代表背景),因此构造的网络图又称为S-T图。
1956年Ford等提出了网络流理论,论证了网络图中的最大流与最小流的等价性。式(1)的能量函数可通过最大流/最小割定理来求解,具体包括增广路径(augmenting paths)法和推进⁃重标记(push-relabel)法。本试验采用后者。
1.2 Graph Cut算法的原理
由于Graph Cuts算法只能分割灰度图像,且参数选择复杂,效率和分割精度较低。因此,Blake等从以下三方面进行了改进,形成Grab Cut算法 :
1) 弃用灰度直方图,转而选用高斯混合模型(GMM 模型)来描述颜色信息的概率分布,实现彩色图像分割;
2) 在GMM模型参数估计过程中,采用可进化的迭代算法取代一次最小估计来完成能量最小化,提高了分割精度;
3) 为了降低用户交互的工作量,通过非完全标号(incomplete labeling)方式(交互中没有指定明确的目标)进行像素标记。该方法只需用户在目标周围画一个矩形框即可。
Grab Cut算法把图像表示为矢量Z= {z1,z2,…,zn,…,zN} ,这样便将图像的分割转化为求每个像素对应的不透明度数组α= {α1,α2,…,αn,…,αN }αN|(αn ∈[0,1]), αn取值为0(背景)或者1(目标),图像目标与背景模型分别用k维的全协方差矩阵GMM表达,通常k=5。向量k={k1,k2,…,kn,…,kN}为每个像素的独立GMM(目标或背景的参数,参数来自目标还是背景,取决于αn的值 ,从而使目标提取问题转化为能量函数的最优化问题,然后采用图割方法求解。
对于RGB空间上的彩色图像,吉布斯(Gibbs)能量函数为:
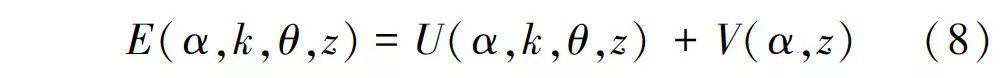
式中:E为能量;U代表数据项; V代表光滑项; α代表不透明度; θ代表图像目标和背景的灰度直方图; z代表图像灰度值数值。数据项U定义为:
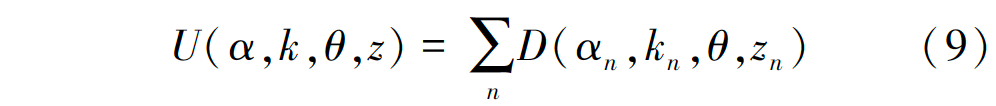
其中, D(αn,kn,θ,zn) = -log p(zn|αn,kn,θ) -
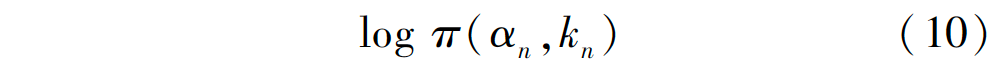
式中: π(•) 代表该高斯模型的样本数在总样本中的混合权重系数; p(•)代表高斯概率分布。所以数据项又可表示为:
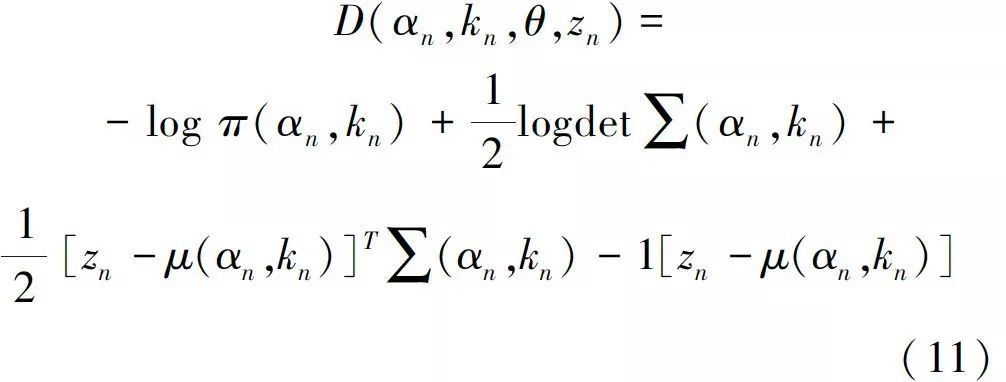
则高斯混合模型的参数模型为:
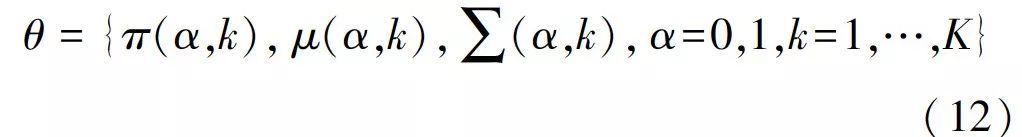
其中: π(α,k)代表每个高斯概率分布的样本数在总样本数中的权值; μ(α,k) 代表高斯模型的均值;

代表协方差; α代表不透明度Alpha值;k代表高斯混合模型参数。
平滑项V可以采用RGB彩色空间的欧几里德距离求得:
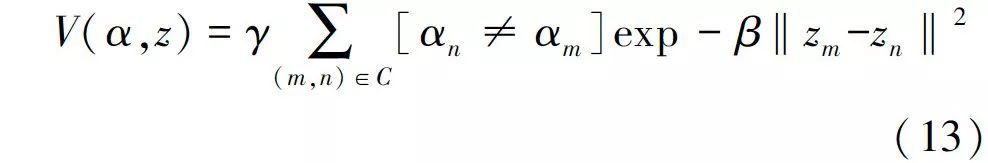
式中:C代表相邻像素对; γ为自适应λ参数; β为常数项。
若把一个更接近真实情况的标记赋予某个像素,则将会惩罚更小的数据项,这样会使总能量函数减少,不断地迭代,最终收敛至最优分割,这样便将Grab Cut算法的图像分割问题转化成求解最小割的问题。
Grab Cut算法的图像分割步骤如图1所示。
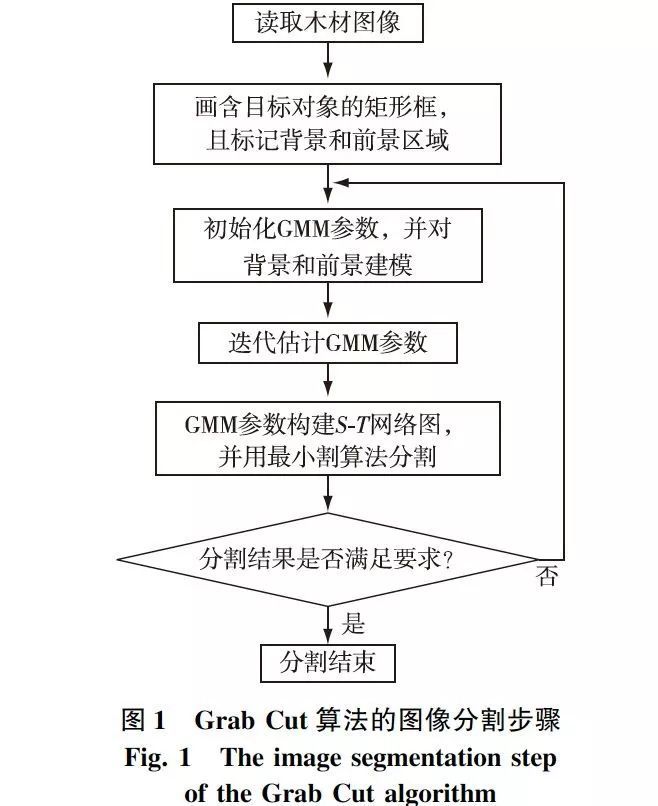
木材表面缺陷图像分割实验
2.1 基于Graph Cuts算法的木材表面缺陷图像分割
本试验采用的计算机为Intel(R) Core(TM)i5-4200U CPU,1.60G硬盘,4G RAM,操作系统为Windows 7 with SP1,编程软件为Visual Studio 2010 C++,OpenCV库。
采用Graph Cuts算法对单缺陷目标图像进行图像分割,木材样本如图2,灰度图像如图3。
2.1.1活节缺陷的图像分割
采用Graph Cuts算法对图3a活节缺陷图像进行分割,参数λ=1。试验中对活节灰度图像进行3次人工种子点标记(其中红色为目标标记,蓝色为背景标记,且标记画笔的半径是5个像素),如图4所示,对应的分割结果如图5所示。
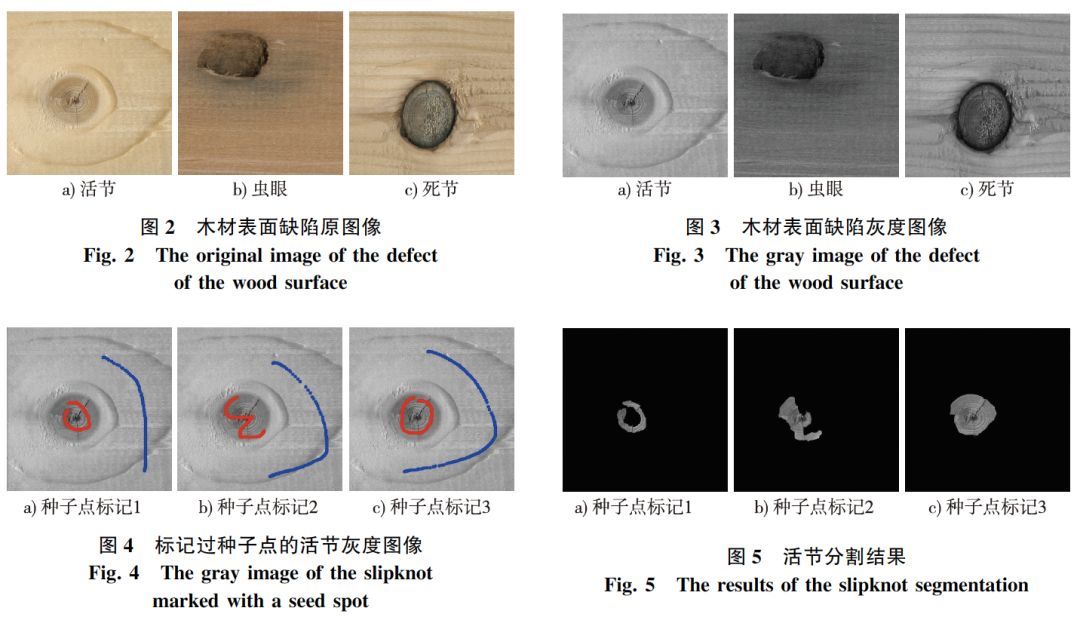
Graph Cuts 算法是基于像素级的分割,不能准确评估像素属于前景或者背景的概率,由于活节缺陷边缘与背景的灰度值差距较小,即使标定的目标种子点像素数量很多(如图4c),但仍存在较严重的欠分割情况。对应图4a、b、c的分割初始化时间分别为41140.06,41022.37和40904.52ms,图像分割所用时间分别为146268.57,278338.17和388243.09ms。可见,种子点素数越多,初始化所用的时间越短,图像分割所用的时间越长。
2.1.2虫眼缺陷的图像分割
采用同样的方法对图3b的虫眼缺陷图像进行分割:设置λ=1,3次人工标记种子点的结果如图6,对应的分割结果如图7。由试验结果可知,虫眼缺陷图像的分割结果与活节缺陷分割相似,分割结果受标定的前景/背景种子点像素数量影响,且都存在一定的欠分割问题。对应图7a、b、c的分割初始化时间分别为41152.20,41038.55和40894.37ms,图像分割时间分别为177052.53,368657.00和417434.91ms。种子点素数越多,初始化所用的时间越短,图像分割所用的时间越长。

2.1.3死节缺陷的图像分割
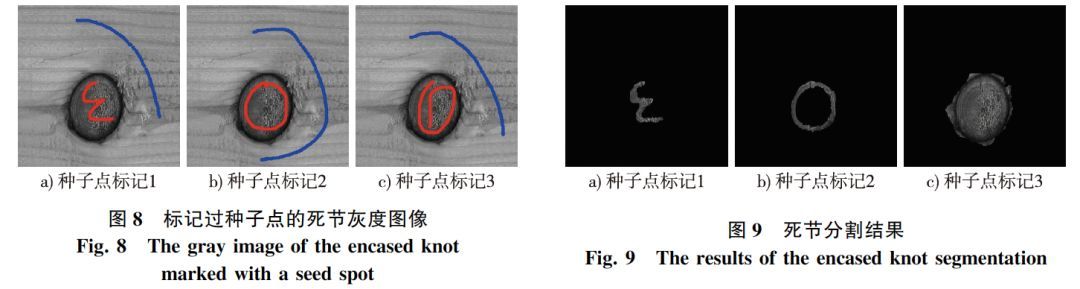
对图3c死节缺陷图像进行分割:设λ=1,3次人工标记种子点的结果如图8,对应的分割结果如图9。可见,采用Graph Cuts算法对标注像素点多的死节缺陷图像能够实现完整分割,但死节缺陷的分割轮廓曲线不平滑,且存在部分过分割情况。对应图8a、b、c的初始化时间分别为40933.91,40921.05和40916.92ms,图像分割所用时间分别为34677.35,371604.00和413967.44ms。
综上所述,采用Graph Cuts算法对木材表面缺陷图像进行分割时,由于Graph Cuts算法对能量函数采用一次性最小化,对目标和背景的人工标记的种子点选取十分重要,选取结果直接影响分割结果;且该算法对相邻像素间的区分度较差,对活节和虫眼缺陷进行分割时存在欠分割问题,对死节缺陷进行分割时出现过分割情况。该算法的初始化时间随种子点标记的像素数的增加而缩短,运行时间相反。
2.2 基于Grab Cut算法的木材表面缺陷图像分割
采用Grab Cut算法对含有单缺陷目标、多缺陷目标的木材表面缺陷图像进行分割试验。试验的参数设定为距离参数β=0.1和GMM更新迭代次数k=5。木材缺陷图像为512×512的彩色图像。在试验过程中,首先输入相同的初始化矩形框。
2.2.1 单缺陷目标的图像分割
1)单活节图像分割:图10a为单个活节样本的原图像,图10b为初始化矩形框,图10d为分割结果,图10c为分割结果的局部放大图,图10e为分割结果与原图像的掩模。虽然活节缺陷的像素灰度值与背景的灰度值的差距较小,但Grab Cut算法仍然可以得到完整的分割轮廓, 分割时间为108144.784ms。由图10e可见,分割结果与原图的吻合度较高,分割效果较好;从图10c分割结果局部放大图可见,Grab Cut算法进行图像分割时,会使活节缺陷内部出现零星的欠分割区域。
2)单虫眼图像分割:图11a为单虫眼样本的原图像,图11b为初始化矩形框,图11d为分割结果,图11c为分割结果的局部放大图,图11e为分割结果与原图像的掩模。虽然活节缺陷的像素灰度值与背景的灰度值的差距较小,但Grab Cut算法仍然可以得到完整的分割轮廓, 分割时间为87329.92ms。由图11e可见,分割结果与原图的吻合度较高,分割效果较好;从图11c分割结果局部放大图可见,Grab Cut算法进行图像分割时,会使虫眼缺陷内部出现零星的欠分割区域。

3)单死节图像分割:图12a为单虫眼样本的原图像,图12b为初始化矩形框,图12d为分割结果,图12c为分割结果的局部放大图,图12e为分割结果与原图像的掩模。虽然活节缺陷的像素灰度值与背景的灰度值的差距较小,但Grab Cut算法仍然可以得到完整的分割轮廓, 分割时间为77545.63ms。由图12e可见,分割结果与原图的吻合度较高,分割效果较好;从图12c分割结果局部放大图可见,Grab Cut算法进行图像分割时,会使虫眼缺陷内部出现零星的欠分割区域。

综上所述,Grab Cut算法进行木材表面缺陷分割,能够得到完整的分割轮廓,且不受背景噪声影响,分割速度快,且对目标与背景像素差别较大的死节和虫眼缺陷分割速度更快,但分割结果均会出现少量的欠分割问题。
2.2.2 多缺陷目标的图像分割
1)多活节缺陷分割试验(图13):图13a为多活节样本的原图像,图13b为初始化矩形框,图13c为分割结果,图13d为分割结果与原图像的掩模。可见,Grab Cut算法能将木材表面的每一个活节缺陷都分割出来,且分割轮廓曲线完整,分割结果与原图的吻合度较高,但在背景中识别出两个过分割噪点,分割时间为13.337s。
2)多虫眼缺陷分割试验(图14):由图14可见,Grab Cut算法能将木材表面的每一个虫眼缺陷都分割出来,且分割轮廓曲线完整,分割效果好,分割结果与原图吻合度较高,分割时间为10.913s。
3) 多死节缺陷分割试验(图15):由图15可见,

Grab Cut算法能将木材表面的每一个死节缺陷都分割出来,且分割轮廓曲线完整,但是右下角死节缺陷的轮廓上存在少量过分割噪点,分割时间为11.634s。
由图13、14、15的分割结果可知,Grab Cut算法能够快速锁定多个木材表面缺陷的边界轮廓,且不受木材表面缺陷的多少、大小和缺陷轮廓形状的影响,分割效果好,分割速度快,抗噪性强,运行时间短。但是Grab Cut算法对木材表面缺陷分割时会出现零星的欠分割或者过分割情况,且分割前需要用户人工画定初始化矩形框。
来自:林业工程学报
- 相关百科
- 相关知识
- 相关专栏
- 建筑给水排水设备器材术语
- 建筑给水排水设计手册(第三版)
- 建筑给水排水设计600问
- 建筑给水系统
- 建筑给水聚乙烯类管道工程技术规程
- 建筑绝热材料的应用类型和基本要求
- 建筑统计
- 建筑维护
- 建筑综合表现技法--计算机建筑表现
- 建筑绿化隔热技术研究
- 建筑网络通信与计算机网络技术应用
- 建筑美
- 建筑美学与室内软装——孙宝宏模式系统设计
- 建筑美学与室内软装:孙宝宏模式系统设计
- 建筑美学对比
- 建筑美学形与意
- 基于压电堆驱动器的喷嘴挡板式气体控制阀
- 磷铵技术改造五大磷肥工程的建议
- 以大豆油多元醇制备的硬质聚氨酯泡沫塑料的性能
- 逆变TIG焊机接触引弧电路的设计(引弧电路)
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 中国工程图学学会成立工程与制造系统集成化分会
- 可替代现有隔热保温材料的新型材料
- 以贯穿项目为核心载体的建筑工程技术专业素材库建设
- 多逆变器太阳能光伏并网发电系统的组群控制方法
- 影响萘高效减水剂与普通硅酸盐水泥适应性的关键因素
- 在全县非煤矿山和危化企业安全生产工作会议上的讲话
- 中国工程造价咨询业的发展趋势
- 支持并行工程和智能CAPP的制造资源建模技术
- 中共重庆市委重庆市人民政府关于建设平安重庆的决定
- 智能建筑工程报警与电视监控系统前端设备的安装施工
- 在“建筑节能与居住舒适”专题技术交流会议上的讲话