矩阵图
矩阵图基本信息
| 中文名 | 矩阵图 | 第一条 | 矩阵图的简要说明 |
|---|---|---|---|
| 第二条 | 制作矩阵图的步骤 | 第三条 | 正文 |
在目的或结果都有二个以上,而要找出原因或对策时,用矩阵图比其他图方便。
矩阵图着眼于由属于行的要素与属于列的要素所构成之二元素的交点:
1.从二元的分配中探索问题的所在及问题的型态。
2.从元的关系中探求解决问题的构想。
在行与列的展开要素中,要寻求交叉点时,如果能够取得数据,就应依定量方式求出;如果无法取得数据时,则应依经验转换成资讯,再决定之,所以决策交叉点时,以全员讨论方式为之,并能在矩阵图旁注上讨论的成员、时间、地点及数据取得方式等简历,以便使用参考。
有时候交叉点的重要度各不相同,因此可用各种记号区别之,例如:
◎ 非常重要或有非常显著关联
○ 重要或有显著关联
△ 有关联
也可以用文字或数据写在交叉点上,使重要度更明确。
矩阵图的应用矩阵图应用比较广泛,一般应用在以下几种情况下:
1. 竞争对手分析时;
2. 新产品策划时;
3. 探索新的课题时;
4. 方针目标展开时;
5. 明确事件关系时;
6. 纠正措施排序时。
矩阵图特点
1. 透过矩阵图的制作与使用,可以累积众人的经验,在短时间内整理出问题的头绪或决策的重点,可以发挥象数据般的效果。
2. 各种要素之间的关系非常明确,能够使我们掌握到全体要素的关系。
3. 矩阵图可根据多次元方式的观察,将潜伏在内的各项因素显示出来。在系统图、关联图、亲和图等手法已分析至极限时使用。
4. 矩阵图依行、列要素分析,可避免一边表现得太抽象、而另一边又太详细的情形发生。
矩阵图造价信息
制作矩阵图一般要遵循以下几个步骤:
①列出质量因素;
②把成对因素排列成行和列,表示其对应关系;
③选择合适的矩阵图类型;
④在成对因素交点处表示其关系程度,一般凭经验进行定性判断,可分为三种:关系密切、关系较密切、关系一般(或可能有关系),并用不同符号表示;
⑤根据关系程度确定必须控制的重点因素;
⑥针对重点因素作对策表。
矩阵图简介
矩阵图法就是从多维问题的事件中,找出成对的因素,排列成矩阵图,然后根据矩阵图来分析问题,确定关键点的方法,它是一种通过多因素综合思考,探索问题的好方法。
在复杂的质量问题中,往往存在许多成对的质量因素,将这些成对因素找出来,分别排列成行和列,其交点就是其相互关联的程度,在此基础上再找出存在的问题及问题的形态,从而找到解决问题的思路。
矩阵图的形式案例,A为某一个因素群,a1、a2、a3、a4、…是属于A这个因素群的具体因素,将它们排列成行;B为另一个因素群,b1、 b2、b3、b4、…为属于B这个因素群的具体因素,将它们排列成列;行和列的交点表示A和B各因素之间的关系,按照交点上行和列因素是否相关联及其关联程度的大小,可以探索问题的所在和问题的形态,也可以从中得到解决问题的启示等。
质量管理中所使用的矩阵图,其成对因素往往是要着重分析的质量问题的两个侧面,如生产过程中出现了不合格时,着重需要分析不合格的现象和不合格的原因之间的关系,为此,需要把所有缺陷形式和造成这些缺陷的原因都罗列出来,逐一分析具体现象与具体原因之间的关系,这些具体现象和具体原因分别构成矩阵图中的行元素和列元素。
矩阵图的最大优点在于,寻找对应元素的交点很方便,而且不会遗漏,显示对应元素的关系也很清楚。矩阵图法还具有以下几个特点:
①可用于分析成对的影响因素;
②因素之间的关系清晰明了,便于确定重点;
③便于与系统图结合使用。2100433B
在目的或结果都有二个以上,而要找出原因或对策时,用矩阵图比其他图方便。
矩阵图着眼于由属于行的要素与属于列的要素所构成之二元素的交点:
1.从二元的分配中探索问题的所在及问题的型态。
2.从元的关系中探求解决问题的构想。
在行与列的展开要素中,要寻求交叉点时,如果能够取得数据,就应依定量方式求出;如果无法取得数据时,则应依经验转换成资讯,再决定之,所以决策交叉点时,以全员讨论方式为之,并能在矩阵图旁注上讨论的成员、时间、地点及数据取得方式等简历,以便使用参考。
有时候交叉点的重要度各不相同,因此可用各种记号区别之,例如:
◎ 非常重要或有非常显著关联
○ 重要或有显著关联
△ 有关联
也可以用文字或数据写在交叉点上,使重要度更明确。
矩阵图的应用矩阵图应用比较广泛,一般应用在以下几种情况下:
1. 竞争对手分析时;
2. 新产品策划时;
3. 探索新的课题时;
4. 方针目标展开时;
5. 明确事件关系时;
6. 纠正措施排序时。
矩阵图特点
1. 透过矩阵图的制作与使用,可以累积众人的经验,在短时间内整理出问题的头绪或决策的重点,可以发挥象数据般的效果。
2. 各种要素之间的关系非常明确,能够使我们掌握到全体要素的关系。
3. 矩阵图可根据多次元方式的观察,将潜伏在内的各项因素显示出来。在系统图、关联图、亲和图等手法已分析至极限时使用。
4. 矩阵图依行、列要素分析,可避免一边表现得太抽象、而另一边又太详细的情形发生。
矩阵图常见问题
-
qc七大手法:关系图法、KJ法、系统图法、矩阵图法、矩阵数据分析法、PDPC法、网络图法的内容是什么
QC7大手法的内容是什么?新QC七大手法 1. 关联图法--TQM推行, 方针管理, 品质管制改善, 生产方式, 生产管理改善 2.KJ法--开发, TQM推行, QCC推行, 品质改善 3. 系统图...
-
现在市场的价格战太离谱了,导致很多的商家都必须用低价来吸引客户,所以产品质量往往都得不到保障。力弘(LHLEEHAM)提供全系列会议视听系统矩阵切换控制器,包含产品有同轴矩阵系列AHD/TVI...
-
首先,接口不同,VGA一般指电脑信号的接口,15芯的一根集成接口和连接电缆,大屏幕一般也都会有,而RGB是指RGBHV接口,(RGB指色度和色差信号的模拟分量信号,HV指行场信号)相当于5根视频线。 ...
制作矩阵图一般要遵循以下几个步骤:
①列出质量因素;
②把成对因素排列成行和列,表示其对应关系;
③选择合适的矩阵图类型;
④在成对因素交点处表示其关系程度,一般凭经验进行定性判断,可分为三种:关系密切、关系较密切、关系一般(或可能有关系),并用不同符号表示;
⑤根据关系程度确定必须控制的重点因素;
⑥针对重点因素作对策表。
矩阵图简介
矩阵图法就是从多维问题的事件中,找出成对的因素,排列成矩阵图,然后根据矩阵图来分析问题,确定关键点的方法,它是一种通过多因素综合思考,探索问题的好方法。
在复杂的质量问题中,往往存在许多成对的质量因素,将这些成对因素找出来,分别排列成行和列,其交点就是其相互关联的程度,在此基础上再找出存在的问题及问题的形态,从而找到解决问题的思路。
矩阵图的形式如下图所示,A为某一个因素群,a1、a2、a3、a4、…是属于A这个因素群的具体因素,将它们排列成行;B为另一个因素群,b1、 b2、b3、b4、…为属于B这个因素群的具体因素,将它们排列成列;行和列的交点表示A和B各因素之间的关系,按照交点上行和列因素是否相关联及其关联程度的大小,可以探索问题的所在和问题的形态,也可以从中得到解决问题的启示等。
质量管理中所使用的矩阵图,其成对因素往往是要着重分析的质量问题的两个侧面,如生产过程中出现了不合格时,着重需要分析不合格的现象和不合格的原因之间的关系,为此,需要把所有缺陷形式和造成这些缺陷的原因都罗列出来,逐一分析具体现象与具体原因之间的关系,这些具体现象和具体原因分别构成矩阵图中的行元素和列元素。
矩阵图的最大优点在于,寻找对应元素的交点很方便,而且不会遗漏,显示对应元素的关系也很清楚。矩阵图法还具有以下几个特点:
①可用于分析成对的影响因素;
②因素之间的关系清晰明了,便于确定重点;
③便于与系统图结合使用。
矩阵图文献

 矩阵图(matrixdiagram)
矩阵图(matrixdiagram)
矩阵图 (matrix diagram) 又名:矩阵 (matrix),矩阵表 (matrix chart) 概述 矩阵图表现为 2组、3组或 4组信息间的关系,同时能提供相关性的更多信息,例如强度、 不同个体的角色或测量方式。 有六种不同形状的矩阵: L 型、T 型、Y 型、X 型、C型和屋顶型, 形状的不同取决于比较组数的多少。这是门类型工具,适用范同很广。 适用场合 ·理解不同组数据间关系时; ·表达不同组数据间的关系时。 一般使用矩阵 ·给一组人分配任务时(有时被称为责任矩阵) : ·将顾客要求与过程因素相联系时(有时叫做关键质量矩阵) ; ·区分哪些问题影响哪些产品或机器的哪个部分时: ·寻找因果关系时; ·寻找将要同时执行的两个计划间的补充和冲突时。 每种矩阵适用场合 表 5.1l概括了每种矩阵的适用场合。 ·L 型矩阵用于 2组间的比较(或与自身的比较) 。 ·T型矩阵用

 质量控制矩阵图
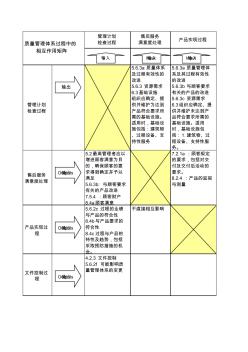
质量控制矩阵图
管理计划 检查过程 售后服务 满意度处理 产品实现过程 管理计划 检查过程 5.6.3a 质量体系 及过程有效性的 改进 5.6.3 资源需求 6.3基础设施 组织应确定、提 供并维护为达到 产品符合要求所 需的基础设施。 适用时,基础设 施包括:建筑物 、过程设备、支 持性服务 5.6.3a 质量管理体 系及其过程有效性 的改进 5.6.3b 与顾客要求 有关的产品的改进 5.6.3c 资源需求 6.3组织应确定、提 供并维护未达到产 品符合要求所需的 基础设施。适用 时,基础设施包 括:1.建筑物、过 程设备、支持性服 务。 售后服务 满意度处理 5.2最高管理者应以 增进顾客满意为目 的,确保顾客的要 求得到确定并予以 满足 5.6.3b: 与顾客要求 有关的产品改进 7.5.4 :顾客财产 8.4a顾客满意 7.2.1a :顾客规定 的要求,包括对交 付及交付后活动的 要求。 8.
矩阵图法在应用上的一个重要特征,就是把应该分析的对象表示在适当的矩阵图上。因此,可以把若干种矩阵图进行分类,表示出他们的形状,按对象选择并灵活运用适当的矩阵图形。常见的矩阵图有以下几种:
(1)L型矩阵图。是把一对现象用以矩阵的行和列排列的二元表的形式来表达的一种矩阵图,它适用于若干目的与手段的对应关系,或若干结果和原因之间的关系。
(2)T型矩阵图。是A、B两因素的L型矩阵和A、C两因素的L型矩阵图的组合矩阵图,这种矩阵图可以用于分析质量问题中"不良现象一原因一工序"之间的关系,也可以用于分析探索材料新用途的"材料成分一特性一用途"之间的关系等。
(3)Y型矩阵图。是把A因素与B因素、B因素与C因素、C因素与A因素三个L型矩阵图组合在一起而形成的矩阵图。
(4)X型矩阵图。是把A因素与B因素、B因素与C因素、C因素与D因素、D因素与A因素四个L型矩阵图组合而形成的矩阵图,这种矩阵图表示A和 B、D,B和A、C,C和B、D,D和A、C这四对因素间的相互关系,如"管理机能一管理项目一输入信息一输出信息"就属于这种类型。
(5)C型矩阵图。是以A、B、C三因素为边做出的六面体,其特征是以A、B、C三因素所确定的三维空间上的点为"着眼点"。
矩阵图法简介
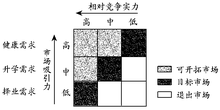
矩阵图法(Matrix Diagram)
矩阵图的形式如下图所示,A为某一个因素群,a1、a2、a3、a4、…是属于A这个因素群的具体因素,将它们排列成行;B为另一个因素群,b1、 b2、b3、b4、…为属于B这个因素群的具体因素,将它们排列成列;行和列的交点表示A和B各因素之间的关系,按照交点上行和列因素是否相关联及其关联程度的大小,可以探索问题的所在和问题的形态,也可以从中得到解 决问题的启示等。
质量管理中所使用的矩阵图,其成对因素往往是要着重分析的质量问题的两个侧面,如生产过程中出现了不合格时,着重需要分析不合格的现象和不合格的原因之间的关系,为此,需要把所有缺陷形式和造成这些缺陷的原因都罗列出来,逐一分析具体现象与具体原因之间的关系,这些具体现象和具体原因分别构成矩阵图中的行元素和列元素。
矩阵图的最大优点在于,寻找对应元素的交点很方便,而且不会遗漏,显示对应元素的关系也很清楚。矩阵图法还具有以下几个特点:
①可用于分析成对的影响因素;
②因素之间的关系清晰明了,便于确定重点;
③便于与系统图结合使用。
矩阵图法的用途十分广泛,在质量管理中,常用矩阵图法解决以下问题:
①把系列产品的硬件功能和软件功能相对应,并要从中找出研制新产品或改进老产品的切入点;
②明确应保证的产品质量特性及其与管理机构或保证部门的关系,使质量保证体制更可靠;
③明确产品的质量特性与试验测定项目、试验测定仪器之间的关系,力求强化质量评价体制或使之提高效率;
④当生产工序中存在多种不良现象,且它们具有若干个共同的原因时,希望搞清这些不良现象及其产生原因的相互关系,进而把这些不良现象一举消除;
⑤在进行多变量分析、研究从何处入手以及以什么方式收集数据。
- 相关百科
- 相关知识
- 相关专栏
- 耐油橡胶
- 丝扣阀门
- 晶体石膏灯
- 对称矩阵
- 高精度液体流量计
- 热水管道泵
- 矩阵式管理
- 橡胶加工基本工艺
- 实用阀门设计手册
- 聚合松香
- 剪切泵
- 仪表阀门
- 橡胶靴鞋制造
- 中国电动工具配件网
- 仪表阀
- 马尔可夫转移矩阵法
- 公称压力PN表示螺栓连接阀盖楔式闸阀力矩参考表
- 基于S3C2440和嵌入式Linux矩阵键盘设计
- 厚壁冷弯方矩管和热轧H型钢轴压极限承载力对比
- 基于直接转矩变频调速技术智能高层电梯控制系统设计
- 履带式起重机力矩限制器安装流程及注意事项图文字说明
- 嘉和广场矩形钢管混凝土框架核心筒超高层性能化设计
- 基于最优传递矩阵层次分析法在桥梁震害评估中应用
- 200立方矩形钢筋混凝土清水池标准图集
- 地基上材料非线性矩形薄板1/3次亚谐共振
- 无粘结部分预应力高强混凝土梁裂缝宽度及闭合弯矩的计算
- 无粘结部分预应力高强混凝土梁例缝宽度及闭合弯矩的计算
- 先张法预应力混凝土管桩抗裂弯矩和极限弯矩计算式
- 国内最大断面矩形顶管在上海轨道交通2号线金科路站开顶
- UCfber在钢筋混凝土截面弯矩曲率计算中应用
- 分形地面与半埋矩形截面目标复合电磁散射FDTD
- 超高矩形薄壁钢管混凝土柱的施工看设计及标准的问题

