角平分线定理
角平分线定理基本信息
| 中文名 | 角平分线定理 | 外文名 | The theorem of angle bisector |
|---|---|---|---|
| 应用学科 | 数学术语 | 范 畴 | 数理科学 |
| 验证方法 | 面积法等 | 学科科目 | 几何学 |
已知,如图4,AM为△ABC的角平分线,求证:
角平分线定理面积法
由三角形面积公式,得
S△ABM=(1/2)·AB·AM·sin∠BAM
S△ACM=(1/2)·AC·AM·sin∠CAM
∵AM是∠BAC的角平分线
∴∠BAM=∠CAM
∴sin∠BAM=sin∠CAM
∴S△ABM:S△ACM=AB:AC
根据:等高底共线,面积比=底长比
可得:S△ABM:S△ACM=MB:MC,则AB:AC=MB:MC
角平分线定理相似法
过C作CN∥AB,交AM的延长线于N
∵CN∥AB
∴∠ABC=∠BCN
又 ∠AMB=∠CMN
∴△ABM∽△NCM
∴AB:NC=BM:CM
∵AM是∠BAC的角平分线
∴∠BAN=∠CAN
又 ∠BAN=∠ANC
∴∠CAN=∠ANC
∴AC=CN
∴AB:AC=MB:MC
(过M作MN∥AB交AC于N也可证明)
角平分线定理正弦定理法
作△ABC的外接圆,AM交圆于D
由正弦定理,得
AB:sin∠AMB=MB:sin∠BAM,
AC:sin∠AMC=MC:sin∠CAM
∵AM是∠BAC的角平分线
∴∠BAM=∠CAM
又∠AMB ∠AMC=180°
∴sin∠BAM=sin∠CAM
sin∠AMB=sin∠AMC
∴AB:AC=MB:MC
角平分线定理造价信息
三角形内外角平分线性质定理:三角形的内外角平分线内、外分对边与其延长线所得的两条线段与夹这个角的两边对应成比例。 2100433B
从一个角的顶点引出的把这个角分成两个相等的角的射线,叫做这个角的角平分线。
三角形的一个角(内角)的角平分线交其对边的点所连成的线段,叫做这个三角形的一条角平分线。
角平分线定理定理1
角平分线上的点到这个角两边的距离相等。
证明:如图1,AD平分∠BAC,DB⊥AB,DC⊥AC
∵AD是∠BAC的平分线
∴∠BAD=∠CAD
∵DB⊥AB,DC⊥AC,垂足分别为B、C
∴∠ABD=∠ACD=90°
又 AD=AD
∴△ABD≌△ACD
∴CD=BD
故原命题得证。
该命题有逆定理:
逆定理:在角的内部到一个角的两边距离相等的点在这个角的角平分线上。
证明:如图,DB⊥AB,DC⊥AC,且DB=DC
∵DB⊥AB,
∴∠DBA=90
同理∴∠DCA=90
在RT△DBA和RT△DCA中,
{DB=DC(已知)
AD=AD(公共边)
∴RT△DBA≌RT△DCA(HL)
∴∠BAD=∠CAD(全等三角形对应角相等)
角平分线定理定理2
三角形一个角的平分线与其对边所成的两条线段与这个角的两边对应成比例。
证明:如图2,在△ABC中,AD是∠BAC的平分线
过点D作DE⊥AB,DF⊥AC
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC
∴DE=DF(定理1)
∵2S△ABD=AB×DE,2S△ACD=AC×DF
∴S△ABD:S△ACD=AB:AC
过点A作AG⊥BC,垂足为G
∵2S△ABD=BD×AG,2S△ACD=CD×AG
∴S△ABD:S△ACD=BD:CD
∴AB:AC=BD:CD
故原命题得证。
该命题有逆定理:
如果三角形一边上的某个点与这条边所成的两条线段与这条边的对角的两边对应成比例,那么该点与对角顶点的连线是三角形的一条角平分线。
证明略。
角平分线定理角平分线长
由定理2和斯特瓦尔特定理可以推导出三角形内的角平分线长公式。
如右图3,在△ABC中,AD平分∠BAC
可设AB=x,AC=y,BD=u,CD=v,则BC=u v
由定理2我们知道 AB:AC=BD:CD,所以xv=uy
由斯台沃特定理,有w²=(x²v y²u)/(u v)-uv
用u=xv/y,v=uy/x替换原式中的u和v
即得AD²=xy-uv=AB×AC-BD×DC
角平分线定理常见问题
-
三角形外角定理证明过程; http://zhidao.baidu.com/question/59352008.html?si=1三角形内角定理:(1)角的平分线是到角的两边距离相等的所有点的集合.∠A...
-
没有圆切角定理,只有弦切角定理:弦切角等于它所夹的弧对的圆周角
-
首先更正一下,是弦切角,老沈瞎说呢。你把图画出来,AB是圆O切线,AC是弦。做过切点A的直径,交圆O于A、D。连接B、D。证明:因为AD是圆O直径,AB是圆O切线所以∠C=90°=∠BAD所以∠BAC...
角平分线定理文献

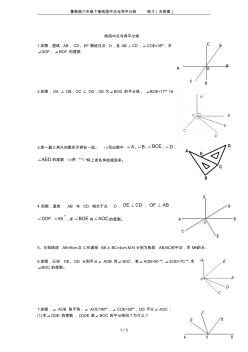 鲁教版六年级下册线段中点与角平分线练习(无答案)
鲁教版六年级下册线段中点与角平分线练习(无答案)
鲁教版六年级下册线段中点与角平分线 练习(无答案) 1 / 3 线段中点与角平分线 1.如图,直线 AB、CD、EF 都经过点 O,且 AB⊥CD,∠COE=35°,求 ∠DOF、∠BOF 的度数. 2.如图,OA 丄 OB,OC 丄 OD,OE 为∠BOD 的平分线, ∠BOE=17° 18 3.把一副三角尺如图所示拼在一起。 ⑴写出图中 A、 B、 BCE、 D、 AED的度数;⑵用 “ ”将上述各角连接起来。 4.如图,直线 AB 与 CD 相交于点 O, CDOE , ABOF , 65DOF ,求 BOE与 AOC的度数。 5、已知线段 AB=6cm,点 C在直线 AB上,BC=4cm,M,N分别为线段 AB,BC的中点 ,求 MN的长 . 6.如图,已知 OE、OD 分别平分∠ AOB 和∠ BOC,若∠ AOB=90°,∠EOD=70°,求 ∠BOC 的度数。 7.如图,

 蝴蝶定理线束夹角表达形式的研究
蝴蝶定理线束夹角表达形式的研究
利用射影几何有关线束与点列的交比关系,给出广义蝴蝶定理的线束夹角的三角函数及斜率表示形式,并且统一给出蝴蝶定理的线段表示新形式.
角平分线长公式公式
三角形ABC的角平分线为AD,D在CB上。则
角平分线长公式推导过程
证明。如图3,延长AC到E,使CE=CD,连接DE,则AE=AC CD,
即
又
则
于是
又
由角平分线定理得
即
代入①中得
证毕。
角平分线长公式公式
在△ABC中,∠A的角平分线记为
其中p是半周长。
角平分线长公式推导过程
证明。法一。如图1,我们先证明
由角平分线定理可得
由余弦定理,
把
即
设
于是
其他角平分线长度同理可证。
证毕。
提要。法二。运用斯特瓦尔特定理,可得证明。
平分三角形一个角的射线与这个角的对边相
交,则顶点和交点之间的线段叫三角形的一
条角平分线。
角分线定理
从角平分线上任意一点到角的两边的距离相等;
角的内部到角的两边的距离相等的点在角的平分线上。
三角形内外角平分线定理
三角形ABC内角A的平分线交线段BC于H,则AB:AC=BH:HC。
三角形ABC的角A的外角的平分线与线段CB的延长线交于H,则AB:AC=BH:HC。
- 相关百科
- 相关知识
- 相关专栏
- 基于PLC控制星三角启动存在问题及解决办法
- 构建对内联接通道发挥北承长江三角洲桥头堡作用
- 化油器三角针阀与阀座导致油耗高与溢油问题解决办法
- 国内外钢结构设计规范关于角焊缝限值及计算方法比较
- 冷拉圆钢、方钢、六角钢
- 柳工挺进长江三角洲扬州柳工建设机械有限公司成立
- 建始县业州镇牛角水村九组通村公路水泥硬化申请报告
- 基于非对称三角模糊数岩石抗剪强度参数确定方法
- 23米三角形钢屋架设计
- GB-T1228-1991钢结构用高强度大六角螺栓范围
- 巡检功能消防联动星三角降压启动水泵电气控制柜控制说明
- CO2气体保护立向下焊技术在船舶上层建筑角接焊中的应用
- 冷拉圆钢、方钢、六角钢尺寸GBT905-1994
- 六角形子午线轮胎钢丝圈双圈挤出缠卷生产线研制开发成功
- 引发角对碳纤维、环氧复合材料圆管件轴向压溃性能的影响
- CAD实现直沟槽成形铣刀不同前角前刃面刃形的转换