计量统计
计量统计基本信息
| 中文名 | 计量统计 | 全 称 | 测量数据的统计分析方法 |
|---|
进行 u 检验、t检验、F 检验等,而对于等级测量水平的数据,一种方法是将它进行转换,用上述方法做近似分析,再一种是用非参数方法进行统计分析。 2100433B
计量统计造价信息
计量统计常见问题
-
你可以导出文件然后拷到可移动硬盘在其他电脑上面打印的啊
-
土建报表中也是有清单工程量的,如果没有是因为你的工程新建的时候没有选择清单
-
用算量软件 在G+工作台下载 安装算量软件
计量统计文献

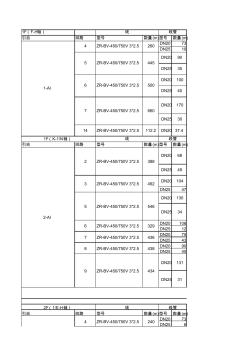 照明统计量
照明统计量
1F(F-H轴) 引自 回路 型号 数量 (m)型号 数量 (m) DN20 73 DN25 10 引自 回路 型号 数量 (m)型号 数量 (m) DN25 47 DN20 106 DN25 12 DN20 75 DN25 43 DN20 90 DN25 40 引自 回路 型号 数量 (m)型号 数量 (m) DN20 73 DN25 6 436 2F(1/E-H轴) 线 线管 9 2-Al ZR-BV-450/750V 3*2.5 434 DN20 37.4 2 ZR-BV-450/750V 3*2.5 388 DN20 68 1F(K-1/N轴) 线 线管 DN25 49 1-Al 6 ZR-BV-450/750V 3*2.5 500 DN20 100 DN25 40 7 ZR-BV-450/750V 3*2.5 660 DN20 170 8 ZR-BV-450/750V 3*2.5

 施工项目统计、计量管理
施工项目统计、计量管理
施工项目统计、计量管理——6.1 一般要求 6.2 报表编制原则 6.3 工程统计管理 6.4 工程计量管理 6.5 对作业队统计、计量资料的要求 …… 附表: 项目经理部建安工作量实际完成情况统计台帐 项目经理部实物工程量实际完成情况统...
统计量样本矩
设x1,x2,…,xn是一个大小为n的样本,对自然数k,分别称 为k阶样本原
点矩和k阶样本中心矩,统称为样本矩。许多最常用的统计量,都可由样本矩构造。例如,样本均值(即α1)和样本方差 是常用的两个统计量,前者反映总体中心位置的信息,后者反映总体分散情况。还有其他常用的统计量,如样本标准差,样本变异系数S/塣,样本偏度,样本峰度等都是样本矩的函数。若(x1,Y1),(x2,Y2),…,(xn,Yn)是从二维总体(x,Y)抽出的简单样本,则样本协方差·及样本相关系数 也是常用的统计量,r可用于推断x和Y的相关性。
统计量次序统计量
把样本X1,x2,…,xn由小到大排列,得到,称之为样本x1,x2,…
,xn的次序统计量。其中最小次序统计量x⑴最大次序统计量x(n)称为极值,在那些如年枯水量、年最大地震级数、材料的断裂强度等的统计问题中很有用。还有一些由次序统计量派生出来的有用的统计量,如:样本中位数 是总体分布中心位置的一种度量,若样本大小n为奇数,,若n为偶数,,它容易计算且有良好的稳健性。样本p分位数Zp(0<p<1)及极差x(n)-x⑴也是重要的统计量。其中Zp当时即为中位数,而当时,表示不超过1 np的最大整数)。样本分位数的一个重要应用是构造连续总体分布的非参数性容忍区间(见区间估计)。
统计量U统计量
这是W.霍夫丁于1948年引进的,它在非参数统计中有广泛的应用。其定义是:设x1,x2,…,xn,为简单样本,m为不超过n的自然数,为m元对称函数,则称 为样本x1,x2,…,xn的以为核的U统计量。样本均值和样本方差都是它的特例。从霍夫丁开始,这种统计量的大样本性质得到了深入的研究,主要应用于构造非参数性的量的一致最小方差无偏估计(见点估计),并在这种估计的基础上检验非参数性总体中的有关假设。
统计量秩统计量
把样本X1,X2,…,Xn 按大小排列为,若 则称Ri为xi的秩,全部n个秩R1,R2,…,Rn构成秩统计量,它的取值总是1,2,…,n的某个排列。秩统计量是非参数统计的一个主要工具。
还有一些统计量是因其与一定的统计方法的联系而引进的。如假设检验中的似然比原则所导致的似然比统计量,K.皮尔森的拟合优度(见假设检验)准则所导致的Ⅹ统计量,线性统计模型中的最小二乘法所导致的一系列线性与二次型统计量,等等。
亦称“估计量”,抽样总体(即样本)计算的统计指标,也就是抽样指标或样本指标。如样本的平均数、众数、中位数、标准差、相关系数等,都是样本统计量。根据这些统计量可以推断总体分布或有关特征数(即总体参数)的可靠性。由于样本是根据随机原则从总体中抽取的,因而样本统计量本身也是一个随机变量,在同一总体的不同样本中,其各自的统计量各有不同,它是随着样本的变化而变化的。
秩统计量(rank statistic)是用于统计检验的一种统计量。是基于样本值的大小在全体样本中所占位次(秩)的统计量。设X1,X2,…,Xn为样本,X(1),X(2),…,X(n)为该样本的顺序统计量。若X1,X2,…,Xn互不相等,则存在惟一的Ri,使Xi=X(Ri),称Ri为Xi之秩。记R=(R1,R2,…,Rn),称R或R的任一已知函数为秩统计量,使用秩统计量的统计方法为秩统计方法,或简称秩方法。特别重要的一类秩统计量是线性秩统计量,即形如:
秩方法主要用于统计检验,称为秩检验。秩方法最主要的优点是由秩方法构造的检验统计量在原假设下往往是分布无关的。
秩方法始自斯皮尔曼(C.Spearman)于1904年使用秩统计量检验两变量是否相关的工作,而威尔柯克松(F.Wilcoxon)于1945年关于秩和检验的工作,则是对秩方法发展史上的一个重要贡献。
- 相关百科
- 相关知识
- 相关专栏
- 计量职能
- 计量误差
- 订价策略决策
- 订单农业运作模式
- 订单农业
- 订单管理
- 订合同
- 订租确认书
- 订立劳动合同须知
- 订货合同
- 订货点法
- 订货点采购
- 订金
- 认房又认贷
- 认知方法学在城市电网规划中的应用研究
- 认知无线电中的射频电调滤波器关键技术研究
- 园林工程计量与计价园路园桥工程计量与计价
- 中国水利水电地下工程数据统计
- 元江县统计局行政效能建设工作总结
- 云南省造价工程师安装计量:除锈、刷油和衬里考试题
- 云南省公路工程工程量清单计量规范B01-2010
- 在35kV及其以下配电网中宜用“计量箱”计量电能
- 广东电网有限责任公司电能计量表箱技术标书
- 关于16定额沟槽管道连接子目套用和计量技术复核记录
- 公路造价师考试技术与计量辅导预制混凝土板考试试卷
- 工程造价工程计量知识整理福建省土石方工程
- 关于做好国有资产评估项目统计工作通知
- 公路造价师考试技术与计量辅导预制混凝土板考试试题
- 公允价值计量模式下投资性房地产转换会计核算
- 公路工程工程量清单计量规则编制说明
- 关于开展既有居住建筑供热计量
- 广西公路造价师技术与计量沥青路面施工方案考试试题