寄存器机
在数理逻辑和理论计算机科学中,寄存器机是以类似于使用图灵机的方式使用的一类抽象机。所有模型都是图灵等价的。寄存器机得名于它有一个或多个"寄存器" -- 替代了图灵机的磁带和磁头,这个模型使用了多个唯一寻址的寄存器,每个都持有一个单一正整数。
图灵机
停机问题
寄存器机造价信息
没有标准术语;每个作者都以自己的助记符或符号下定义。
寄存器机构成如下:
1 无界数目的标定的、离散的、在宽度(容量)上无界的寄存器:
有限(在某些模型中无限)的寄存器集合 '0 ... '',每个都有无限宽度并持有一个单一非负整数 (0, 1, 2, ...)。寄存器可以做它们自己的算术,或者可以有也可以没有一个或多个做算术的特殊寄存器,比如"累加器"或"地址寄存器"。
2 计数的筹码或标码 -- 离散的、不可细分的唯一一类只适合这个模型的物件或标记。
在最精简的计数器机模型中,对每个算术指令只有一个物件/标记被要么增加到要么减少自它的位置/磁带。在某些计数器机模型(比如 Melzak (1961), Minsky (1961))和多数 RAM 与 RASP 模型中,在"加法"、"减法"、"乘法"和"除法"这样的指令中多于一个物件/标记可以增加或减少。某些模型有控制运算比如"复制"(也叫做"移动"、"装载"、"存储")一个动作就从寄存器到寄存器移动一堆物件/标记。
3 (非常)有限的指令集:
指令可被分类 -- 3.1 算术和 3.2 控制。对指令集有一种限制: 一个指令集必须允许这个模型是图灵等价的,就是说它必须能够计算任何偏递归函数:
3.1 算术
算术指令可以运算于所有寄存器上或只在特殊的寄存器上(比如累加器)。他们通常被按如下集合来选择(但例外大量存在):
*计数器机: { 增加 (r), 减少 (r), 清零 (r) }
*精简 RAM, RASP: { 增加 (r), 减少 (r), 清零 (r), 装载立即常量 k, 加 (r1,r2), 真减 (r1,r2), 增加累加器, 减少累加器, 清除累加器, 加寄存器 r 的内容到累加器, 从累加器真减寄存器 r 的内容 }
*扩充 RAM, RASP: 所有精简指令加上: { 乘法, 除法, 各种布尔逐位运算 (左移位, 位测试, 等等)}
3.2 控制:
计数器机模型: 可选的 { 复制 (r1,r2) }
RAM 和 RASP 模型: 多数都有 { 复制 (r1,r2) }, 或 { 装载累加器从 r, 存储累加器到 r, 装载立即常量到累加器 }
所有模型: 至少一个跟随寄存器测试的条件"跳转"(分支,goto),比如 { 零时跳转, 非零时跳转(就是,正时跳转), 等时跳转, 非等时跳转 }
所有模型可选的: { 无条件程序跳转 (goto) }
3.3 寄存器寻址方法:
计数器机: 没有间接寻址,在高度原子化的模型中可能有立即操作数
RAM 和 RASP: 可用间接寻址,典型的立即操作数
3.4 输入输出:
所有模型: 可选的
4 状态寄存器:
一个特殊的指令寄存器 "IR",有限并独立于上述寄存器,它存储当前的要执行的指令和它在指令 TABLE(表格) 中的地址;这个寄存器和它的 TABLE 位于有限状态机内。
注释 #1: IR 是对于所有模型都是禁区。在 RAM 和 RASP 的情况下,为了确定一个寄存器的地址,模型可以选择要么 (i)在直接寻址的情况下 -- 地址通过 TABLE 指定而临时位于 IR 中,或 (ii) 在间接寻址的情况下 -- 寄存器的内容由 IR 的指令指定。
注释 #2: IR 不是 RASP (或常规计算机)的程序计数器(PC)。PC 只是类似累加器的另一个寄存器,只专门持有 RASP 的当前基于寄存器的指令的编号。所以 RASP 有两个"指令/程序"寄存器 -- (i) IR (有限状态自动机的指令寄存器) 和 (ii) PC (程序计数器) 用于位于寄存器中的程序。(同样于专门的 PC 寄存器,RASP 可以有专门的寄存器如"程序-指令寄存器"(用名字如 "PIR, "IR", "PR" 等)
5 通常按顺序的标定指令的列表:
指令的有限列表 '1 ... ''。在计数器机、随机存取机(RAM)和指针机的情况下,指令存储于有限状态机的 TABLE 中;因此这些模型是哈佛结构的例子。在 RASP 的情况下,程序存储在寄存器中;所以它是冯·诺伊曼结构的例子。
通常像计算机程序,指令被按顺序列出;除非成功跳转否则缺省顺序是眼数值次序。有个例外是算盘(Lambek (1961), Minksy (1961))计数器机模型 -- 所有指令都有至少一个"下一个"指令标识符 "z",而条件分支有两个。(算盘模型组合了两个指令 JZ 接着 DEC):
比如 { INC ( r, z ), JZDEC ( r, ztrue, zfalse ) }.
寄存器机常见问题
-
寄存器是cpu的一部分,是计算机中速度最快的存储器,分为 通用寄存器、专用寄存器、段寄存器、其他寄存器,每个寄存器存储一种类型的变量,各司其职,这样说来,又分为累加器、源变址寄...
-
指令寄存器的作用: 通常都用来意指由一个指令之输出或输入可以直接索引到的暂存器群组。 寄存器是中央处理器内的组成部份。寄存器是有限存贮容量的高速存贮部件,它们可用来暂存指令、...
-
是一类应用很广的时序逻辑电路,通过本知识点的学习理解移位寄存器的概念和工作原理,学会通过功能表来分析模块的逻辑功能
寄存器机文献

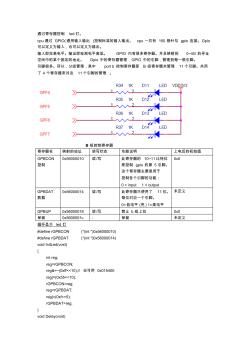 嵌入式ARM9通过寄存器控制led灯
嵌入式ARM9通过寄存器控制led灯
通过寄存器控制 led灯。 cpu通过 GPIO(通用输入输出 )控制标准的输入输出。 cpu 一共有 150 根针与 gpio 连接。Gpio 可以定义为输入,也可以定义为输出。 输入即拉高电平。输出即检测电平高低。 GPIO 内有很多寄存器。并且映射到 0~4G 的寻址 空间中的某个固定的地址。 Gpio 中的寄存器管理 GPIO 中的引脚,管理到每一根引脚。 引脚很多。所以,分组管理,其中 port b 控制寄存器即 B 组寄存器共管理 11个引脚。共用 了 4 个寄存器来对这 11个引脚的管理 。 B 组控制寄存器 寄存器名 映射的地址 读写状态 功能说明 上电后的初始值 GPBCON 控制 0x56000010 读 /写 此寄存器的 10~11比特位 即控制 gpio 的第 5 引脚。 这个寄存器主要是用于 控制各个引脚的功能: 0 = input 1 = output 0x0

 基于可逆触发器的可逆移位寄存器设计方法
基于可逆触发器的可逆移位寄存器设计方法
为了进一步提高可逆时序逻辑电路设计方法的通用性和改善可逆电路性能指标,以可逆主从D触发器为基本单元,通过将时钟信号及垃圾位信号级联再利用,提出了一种可逆串行移位寄存器优化设计方案。在此基础上,通过目标函数构造及变换构建带有移位控制的单元模块,设计了满足串行输入串/并行输出功能的n位可逆双向移位寄存器。设计结果表明,采用方法所设计的可逆移位寄存器具有较优的性能指标,且对于双向移位寄存器综合具有较好的通用性。
作为用于形式逻辑和理论计算机科学中的计算模型,计数器机是寄存器机模型的最原始的子类。
它只由如下组成:(i)一序列的一个或多个(唯一性)命名的"无界"寄存器(只包含一个单一无界正整数的寄存器),(ii)假如到或减去自寄存器的叫做"计数器"的物件,(iii)让计算机(人或机器)服从的(通常顺序的)算术和控制指令的列表。
对于给定的计数器机模型,指令集是非常微小的,只有从 1 到 6 或 7 指令。所有模型都包含一些算术运算和至少一个"条件表达式"(IF-THEN-ELSE)。三个基本模型,每个都使用了三个指令,从下列指令中划分出来(简写助记符是任意的):
停机(HALT)指令可以包含也可以不包含在模型中。
三个计数器机的计算能力是等价的 -- 一个模型的指令可以从其他模型的指令得出。都等价于图灵机的计算能力(但只有用哥德尔数来编码在计算器中的数据,否则它们的能力等价于原始递归函数)。由于它们的一元处理方式,计数器典型的要比图灵机慢一个因子,它是在相比较的图灵机使用的空间的指数。
计数器机模型还有一些其他的名字: Shepherdson-Sturgis 机, Minsky 机, 程序机, 算盘机 , Lambek 机, 后继机 等等。详情参见计数器机模型。
- 相关百科
- 相关知识
- 相关专栏
- 土工膜渗透系数测定仪
- Window性能计数器
- 家具打磨台
- 带电电荷量测试方法
- 单片机控制技术
- 吊钩式抛丸清理机
- 工业气体报警器
- 轮盘计数器
- 科群防辐射产品网
- ZH7811型液体比热容测定仪
- ABS磨粉机
- 热缩管切割机
- 手持式激光粒子计数器
- LED登录模块计数器
- 超声波压电陶瓷片
- PET瓶垂直载压测定仪
- 柴油机高压喷油管用钢、高压喷油管及其制造方法
- 印度EPC电站项目竞标中降低汽轮机热耗的策略
- 云南绿水河二级电站4号水轮机增容技术改造效果分析
- 在数控机床上通过监视主轴电机负荷实时监控刀具寿命
- 一拖多变频空调产品测试系统与室外机通信接口
- 以电动葫芦为起升机构的简易强制式升降机钢丝绳检验
- 永磁同步电机-空调压缩机系统的无传感器过调制控制
- 应用新型高性能水轮机转轮对老电站水电机组增容改造
- 医疗垃圾破碎机破碎装置的结构设计含全套CAD图纸
- 中国管状电机行业市场前景分析预测年度报告(目录)
- 应用PC—1500机计算水工建筑物厚壁结构的内力
- 以合成烃为基础油研制的机车螺杆式空气压缩机润滑油
- 制作质量对塔式起重机结构件焊接节点疲劳性能的影响
- 公路工程施工、桥涵施工工艺大全造桥机造桥工艺流程
- 基于RS485总线技术PC机与单片机多机通讯设计
- 基于VB6.0太阳能发电基站电源上位机软件设计