角角边
角角边基本信息
| 中文名 | 角角边 | 外文名 | the AAS law of congruence |
|---|---|---|---|
| 应用学科 | 几何 | 适用范围 | 主要在平面三角形和球面三角形 |
| 简 称 | AAS | 属 性 | 两个三角形全等 |
已知:△ABC和△A'B'C'.∠A=∠A',∠B=∠B',BC=B'C'.
求证:△ABC≌△A'B'C'.
证明:考虑解三角形的过程.已知△ABC的A,B,a,求C,b,c.
由三角形内角和为180°,得C=180°-A-B.
由正弦定理得,a/sinA=b/sinB,故b=asinB/sinA.
由余弦定理得,c²=a² b²-2abcosC.由于C=180°-A-B,b=asinB/sinA,c>0,故c有唯一的值.
综上,C,b,c有唯一的值.即已知△ABC的A,B,a,则△ABC的六个元素(A,B,C,a,b,c)都是唯一确定的,即△ABC有唯一解.
故△ABC和△A'B'C'经平移旋转后可以重合,即△ABC≌△A'B'C'.
角边角定理的证明是类似的.已知三角形的两角就可以知道三角形的形状,再知道一边即可确定三角形的大小.2100433B
角角边造价信息
所谓角角边定理,就是两角及其中一角的对边对应相等的两个三角形全等,简称“角角边”“AAS”(A:angle,角;S:side,边)。
角角边常见问题
-
角角边可以,简写为AAS边边角不行,因为会出现两种情况。但是在直角三角形中,有一条斜边和直角边对应想等的三角形全等,简写为HL
-
对的
-
不能 ,找个很简单的例子假定钝角三角形ABC, 角A=120度,B为 15度,C为 45度过A向BC做垂线,交于D,然后在 DB之间选择点E,使得 ED=DC显然三角形AEB和ACB满足角B=角BAB...
角角边文献

 换个角度看“边边角”--证明两个钝角三角形全等
换个角度看“边边角”--证明两个钝角三角形全等
在“边边角”的课堂上,当我发现了“两边及其中一边的对角对应相等的两个直角三角形全等”和“两边及其中一边的对角对应相等的两个锐角三角形全等”是真命题后,我随即就猜想“两边及其中一边的对角对应相等的两个钝角三角形全等”,但后来和陈老师一起探索才发现,原来用“边边角”证明两个钝角三角形全等是有前提条件的,即“两边及其中一边的对角对应相等的两个钝角三角形,若另一对应相等的边所对的角都是锐角或都是钝角,则这两个钝角三角形全等,否则这两个钝角三角形不全等”。对于“若另一对应相等的边所对的角都是锐角或都是钝角”这个条件,我发现了还可以换成其他条件,下面将我的探索与发现汇报如下。

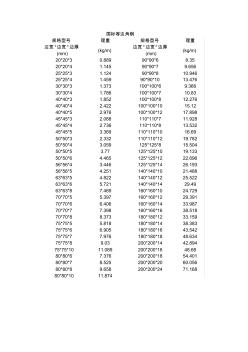 国标等边角钢
国标等边角钢
国标等边角钢 规格型号 理重 规格型号 理重 边宽 *边宽 *边厚 (mm) (kg/m) 边宽 *边宽*边厚 (mm) (kg/m) 20*20*3 0.889 90*90*6 8.35 20*20*4 1.145 90*90*7 9.656 25*25*3 1.124 90*90*8 10.946 25*25*4 1.459 90*90*10 13.476 30*30*3 1.373 100*100*6 9.366 30*30*4 1.786 100*100*7 10.83 40*40*3 1.852 100*100*8 12.276 40*40*4 2.422 100*100*10 15.12 40*40*5 2.976 100*100*12 17.898 45*45*3 2.088 110*110*7 11.928 45*45*4 2.736 110*110
- 相关百科
- 相关知识
- 相关专栏
- 植被混凝土在水利边坡工程中进展和应用现状
- 格构梁与锚索注浆复合结构在加固边坡工程中应用
- 基于PLC控制星三角启动存在问题及解决办法
- 基于FlAC3D强度折减法露天煤矿边坡稳定性分析
- 构建对内联接通道发挥北承长江三角洲桥头堡作用
- 工业景观复合性设计白云边工业园规划与建筑设计
- 化油器三角针阀与阀座导致油耗高与溢油问题解决办法
- 基于DEM-LEM考虑裂隙扩展岩质边坡稳定性分析
- 国内外钢结构设计规范关于角焊缝限值及计算方法比较
- 基于ABAQUS强度折减法边坡稳定性影响因素分析
- 冷拉圆钢、方钢、六角钢
- 某国道线边坡防护TECCO钛克防护网设计施工图说明
- 柳工挺进长江三角洲扬州柳工建设机械有限公司成立
- 建始县业州镇牛角水村九组通村公路水泥硬化申请报告
- 基于非对称三角模糊数岩石抗剪强度参数确定方法
- 基于突变级数法高速公路路堑高边坡施工安全风险评价