简化测度

简化测度（reduced measure）是一般位势论中简化函数的类似物，简化测度也是超过测度。

简化测度性质
简化测度造价信息
简化测度简化函数
简化测度简介
简化测度常见问题
简化测度文献
测度问题简介
测度问题发展
测度问题性质

简化测度基本信息

中文名	简化测度	外文名	reduced measure
适用范围	数理科学

简化测度性质

也是超过测度，

且在G上

。

超过测度的里斯分解式

满足

。若G是相对紧的开集，则

是一个位势。

特别地，

是一个位势，所以存在惟一的σ(G)∈G(χ)，使得

。

查看详情

简化测度造价信息

市场价

信息价

询价

材料名称	规格/型号	市场价（除税）	工程建议价（除税）	品牌	单位	税率	供应商
球墨铸铁双盘简化短管	DN600/DN600	查看价格	查看价格		个	13%	泽州县世纪球墨铸造有限公司保定销售处
M随心配镜柜	K-15512T-NL/NR-NA 489mm简化版-左开门/右开门	查看价格	查看价格		个	13%	科勒(中国)投资有限公司
浴室家具	15512T-NR-NA 20寸M随心配镜柜(简化版右开门)/15512T-NR-NA	查看价格	查看价格	科勒	套	13%	北京建贸新科建材有限公司
远程控制器	产品号:537100-B21 针对1路服务器的简化标准版适用范围:ML110G7/DL120G7	查看价格	查看价格		套	13%	广州昊群计算机科技有限公司
48口接入交换机	包转发速率:≥17Mpps;交换容量:≥64Gbps;支持百兆电端口≥48个千兆电口≥2个千兆光口≥2个;为简化管理要求设备支持堆叠;	查看价格	查看价格	华为	个	13%	深圳市众盈创达科技有限公司
接入交换机	包转发速率:≥17Mpps;3.交换容量:≥64Gbps;4.支持百兆电端口≥48个千兆电口≥2个千兆光口≥2个;5.为简化管理要求设	查看价格	查看价格	锐捷	个	13%	深圳市联通华程通信技术有限公司
镜柜	品名描述:M随心配系列镜柜简化版-489mm(右开门);产品规格:489×116×762mm;产品体积:0.13;型号:K-15512T-N	查看价格	查看价格	科勒	个	13%	华艺经典(北京)厨卫科技发展有限公司
无线手持话筒	摇一摇自动对频彻底简化复杂的工程安装为客户定制提供了无限可能;新增一键电音功	查看价格	查看价格	BBS	个	13%	北京卓邦电子技术有限公司

材料名称	规格/型号	除税信息价	含税信息价	行情	品牌	单位	税率	地区/时间
暂无数据

材料名称	规格/需求量	报价数	最新报价（元）	供应商	报价地区	最新报价时间
承插简化短管	DN100\|1个	2	查看价格	佛山市汴津钢铁有限公司		2015-03-26
双盘简化短管DN400	球墨铸铁\|1个	1	查看价格	天津华泰旺鑫钢铁贸易有限公司	天津天津市	2015-06-15
双盘简化短管DN80	球墨铸铁\|1个	1	查看价格	天津华泰旺鑫钢铁贸易有限公司	天津天津市	2015-06-15
铸铁盘插简化短管	DN150\|1个	2	查看价格	佛山市汴津钢铁有限公司		2015-03-26
自动化监控系统-NH3-N测度仪	0-320mg/L(详见自控图)\|1套	1	查看价格	深圳市爱乐尼特仪器有限公司	广东	2021-08-26
无线话筒(一拖二)	型号:KT-628/HC 内置60组频率模组,简化用户调频程\|1台	3	查看价格	广州市熹尚科技设备有限公司	全国	2021-10-26
无线头戴话筒(一拖二)	型号:KT-628/HH 内置60组频率模组,简化用户调频程\|1套	3	查看价格	广州市熹尚科技设备有限公司	全国	2021-10-26
椭圆茶几1件	实木框架+木饰面,桌面简化,只做木纹斜拼,不做花型造型.(1400×780×450mm)\|1件	3	查看价格	成都喻丽兰家具有限公司	四川	2022-06-20

简化测度简化函数

简化函数是在一个子集上不小于一个给定函数的一族函数的下确界。

设Φ是一族从Ω到[0, ∞]的下半连续的函数u所组成的凸锥（必要时设 ∞∈Φ），f为E(E⊂Ω)到[0, ∞]的函数，令

=inf{u(x)|u∈Φ且u|E≥f}（对空集∅，令

=0)，称之为f到E的简化函数。2100433B

查看详情

简化测度简介

简化测度是一般位势论中简化函数的类似物。

设G是开集，ξ是超过测度，那么测度

=inf{μ|μ是超过测度且在G上μ≥ξ}称为ξ在G上的简化测度。

查看详情

简化测度常见问题

简化预算问题

如果那样的话造价人员还有存在的意思么? 计算机都能做了，人的价值就没了当然未来的事情很可能会发展到那一块
标高设置如何简化？

没有复制前不要修改梁的标高，让梁标高按楼层，复制后也是按楼层的
简化多栋同类型房屋计算。

简化多栋同类型房屋计算。目前做一个项目，10多栋房子，有很多相似的地方，结构上：砖混和底框均有。户型：abc三种。目前已经做了几栋了，想利用下现成的模板。我的回答：建议直接做ABC三种户型进行汇总计...

简化测度文献

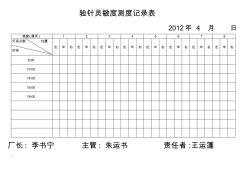验针灵敏度测度记录表

格式：pdf

大小：31KB

页数： 2页

评分： 4.6

验针灵敏度测度记录表 2012年 4 月日高度 (厘米 ) 1 2 3 4 5 6 7 8 灯亮点数位置时间左中右左中右左中右左中右左中右左中右左中右左中右 8:00 10:00 14:00 16:00 19:00 厂长 : 李书宁主管 : 朱运书责任者 :王运蓬验针灵敏度测度记录表 2012年 4 月日高度 (厘米 ) 1 2 3 4 5 6 7 8 灯亮点数位置时间左中右左中右左中右左中右左中右左中右左中右左中右 8:00 10:00 14:00 16:00 19:00 厂长 : 李书宁主管 : 朱运书责任者 :王运蓬

立即下载

挤压筒的简化设计

格式：pdf

大小：31KB

页数： 3页

评分： 4.3

挤压筒是铜材生产的关键模具之一,工作时需要承受高温、高压、高摩擦的作用。本文从挤压筒的结构、选材及强度校核几方面,通过分析计算,提出了挤压筒简化计算的原理,在实际使用中取得了显著的经济效益。

立即下载

测度问题简介

测度问题是测度论中的著名问题。

对于直线而论，人们总希望直线上某个测度，关于它可测的集合越多越好。可测集多，意味着可测函数多，从而可积函数也多。对于平面或高维空间的情形也是这样。

所谓测度问题，就是（直线上）是否存在具有下列性质的测度：

1、具有可列可加性；

2、（直线上的）所有子集都可测；

3、具有平移不变性；

4、[0,1]的测度是1。

查看详情

测度问题发展

测度问题是勒贝格(Lebesgue,H.L.)于1904年提出的，这个问题已经解决，结论如下：去掉测度论性质2,3,4中任何一条，容易举例说明满足其余三条的测度是存在的。性质1,2,3,4全都满足的测度是不存在的，特别地，直线上必存在不是勒贝格可测的集，这首先是由维塔利(Vitali,G.)于1905年指出的。

查看详情

测度问题性质

如果将测度问题性质1换成1'：具有有限可加性，则满足1',2,3,4的测度是存在的，但不惟一，这就是著名的巴拿赫定理。

对于空间Rⁿ(n≥2)，则有结论：

当n=2时，满足1',2,3,4的测度是存在的。

当n≥3时，满足1',2,3,4的测度是不存在的。

这个问题是由豪斯多夫(Hausdorff,F.)于1914年提出并于1923年解决的。 2100433B

查看详情

简化测度相关推荐

相关百科
相关知识
相关专栏

百科

简化测度

简化测度基本信息

简化测度性质

简化测度造价信息

简化测度简化函数

简化测度简介

简化测度常见问题

简化测度文献

测度问题简介

测度问题发展

测度问题性质

最新词条