积分电路是使输出信号与输入信号的时间积分值成比例的电路。最简单的积分电路由一个电阻R和一个电容C构成,如图(a)所示。若时间常数RC足够大,外加电压时,电容C上的电压只能慢慢上升。在t<
u 0(t)= ∫i/Cdt ≈∫u i(t)/RCdt = t*u i(t)/RC
即输出电压近似与输入电压的时间积分值成比例。如果输入信号U
i(t)是一个阶跃电压,理想积分电路的输出是一线性斜升电压,如图(b)虚线所示。简单的RC积分电路的实际输出波形与理想情况不同,在t<
积分电路还可以用于处理模拟信号。当输入为正弦信号 u i(t)=Um 时,积分电路的输出为
u 0(t)=1/RCdt=Um/ωRC
其幅度为输入信号的1/ωRC,相位落后90°。当输入信号含有不同频率分量时,积分电路输出端的信号中频率较高的分量所占的比例降低。在间接调频器中,为了用调相电路得到调频波,先用积分电路对调制信号积分,后由调相电路对载波进行相位调制,得到调频波。
积分电路模拟电路
电路型式
图①是反相输入型积分电路,其输出电压是将输入电压对时间的积分值除以时间所得的商,即Vout=-1/C1R1∫Vin dt,由于受运放开环增益的限制,其频率特性为从低频到高频的-20dB/dec倾斜直线,故希望对高频率信号积分时要选择工作频率相应高的运放。
图②是差动输入型积分电路,将两个输入端信号之差对时间积分。其输出电压Vout=1/C1R1∫(Vin2-Vin1)dt;若将图②的E1端接地,就变成同相输入型积分电路。它们的频率特性与图1电路相同。
积分电路参数选择
主要是确定积分时间C1R1的值,或者说是确定闭环增益线与0dB线交点的频率f0(零交叉点频率),见图③。当时间常数较大,如超过10ms时,电容C1的值就会达到数微法,由于微法级的标称值电容选择面较窄,故宜用改变电阻R1的方法来调整时间常数。但如所需时间常数较小时,就应选择R1为数千欧~数十千欧,再往小的方向选择C1的值来调整时间常数。因为R1的值如果太小,容易受到前级信号源输出阻抗的影响。
根据以上的理由,图①和图②积分电路的参数如下:积分时间常数0.2s(零交叉频率0.8Hz),输入阻抗200kΩ,输出阻抗小于1Ω。
积分电路更多相关
电路结构如图J-1,积分电路可将矩形脉冲波转换为锯齿波或三角波,还可将锯齿波转换为抛物波。电路原理很简单,都是基于电容的充放电原理,这里就不详细说了,这里要提的是电路的时间常数R*C,构成积分电路的条件是电路的时间常数必须要大于或等于10倍于输入波形的时间宽度。输出信号与输入信号的积分成正比的电路,称为积分电路。
原理:从图得,Uo=Uc=(1/C)∫icdt,因Ui=UR Uo,当t=to时,Uc=Oo.随后C充电,由于RC≥Tk,充电很慢,所以认为Ui=UR=Ric,即ic=Ui/R,故
Uo=(1/c)∫icdt=(1/RC)∫Uidt
这就是输出Uo正比于输入Ui的积分(∫Uidt)
RC电路的积分条件:RC≥Tk
积分电路造价信息
右图是一个典型的积分电路图。由图可以看出,输入信号经过了一个电阻后经过反馈流到电容上,但此时认为电容的初始电量为零,故此时给电容充电。由理想运算放大器的虚短、虚断性质得,(vi-0)/R=dQ/dt=C*d(0-vo)/dt,所以vo=-1/(RC)∫ vdt.
如果把R1和C换个位置,就成了微分电路(但输入的电压应该是交流信号才可通过电容)。
上面讨论的运算放大器是基于电压放大器基础之上的。
积分电路原理常见问题
-
电路型式图①是反相输入型积分电路,其输出电压是将输入电压对时间的积分值除以时间所得的商,即Vout=-1/C1R1∫Vin dt,由于受运放开环增益的限制,其频率特性为从低频到高频的-20dB/dec...
-
微分电路可把矩形波转换为尖脉冲波,主要用于脉冲电路、模拟计算机和测量仪器中,以获取蕴含在脉冲前沿和后沿中的信息,例如提取时基标准信号等。积分电路使输入方波转换成三角波或者斜波,主要用于波形变换、放大电...
-
一.积分电路原理以及定义积分电路是使输出信号与输入信号的时间积分值成比例的电路。最简单的积分电路由一个电阻R和一个电容C构成,如图(a)所示。若时间常数RC足够大,外加电压时,电容C上的电压只能慢慢上...
积分电路原理文献

 《电路原理》作业
《电路原理》作业
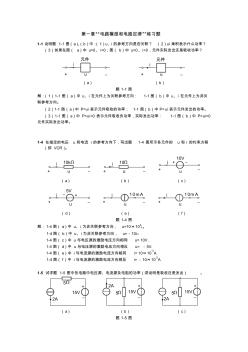
第一章“电路模型和电路定律”练习题 1-1 说明题 1-1 图(a)、(b)中:( 1)u、i 的参考方向是否关联? ( 2)ui 乘积表示什么功率? (3)如果在图( a)中 u>0、 i<0;图( b)中 u>0、 i>0,元件实际发出还是吸收功率? i u+ 元件 i u+ 元件 (a) (b) 题 1-1 图 解:(1)1-1 图( a)中 u、 i 在元件上为关联参考方向: 1-1图( b)中 u、 i 在元件上为非关 联参考方向。 (2)1-1 图(a)中 P=ui 表示元件吸收的功率; 1-1 图(b)中 P=ui 表示元件发出的功率。 (3)1-1 图( a)中 P=ui<0 表示元件吸收负功率,实际发出功率: 1-1图( b)中 P=ui>0 元件实际发出功率。 1-4 在指定的电压 u 和电流 i 的参考方向下,写出题 1-4 图所示各元件的 u 和 i 的约束方程

 声控灯设计电路原理
声控灯设计电路原理
声光控延时照明灯的设计 一、设计背景 本次设计是以实践性为课题, 起到巩固所学知识, 加强综合能力,培养电路设计能力, 提高实验技术,启发创新思想的效果。 用声光控延时开关代替住宅小区的楼道上的开关, 只有在天黑以后,当有人走过楼梯 通道,发出脚步声或其它声音时, 楼道灯会自动点亮, 提供照明,当人们进入家门或走出 公寓,楼道灯延时几分钟后会自动熄灭。在白天,即使有声音,楼道灯也不会亮,可以达 到节能的目的。声光控延时开关不仅适用于住宅区的楼道,而且也适用于工厂、办公楼、 教学楼等公共场所,它具有体积小、外形美观、制作容易、工作可靠等优点。 二、总体方案设计 电路由直流供电电路、控制电路、延时电路三部分组成。控制电路采用基本数字逻辑 单元进行设计。 直流供电电路 由 D1-D4组成桥式整流电路。交流 220V电压经桥式整流桥后变成脉 动的直流电,供后续电路工作。 控制电路由四与非门 CD4
积分运算和微分运算互为逆运算,在自控系统中,常用积分电路和微分电路作为调节环节;此外,他们还广泛应用于波形的产生和变换以及仪器仪表之中。以集成运放作为放大电路,利用电阻和电容作为反馈网络,可以实现这两种运算电路。2100433B

积分运算电路积分电路应用

罗氏线圈Rogowski Coil积分电路
根据电磁感应定律及安培环路定理,罗氏线圈输出感应电动势与一次电流变化率成正比。也就是其输出电压与电流的微分成正比,因此,采用微分的逆运算--积分可以将输出还原为与输入一次电流成正比的电压信号,通过测量该信号,可以更加直接的反映一次电流。
除了固定且已知频率的标准正弦波之外,测量时,罗哥夫斯基线圈需要与积分器配套使用。由于罗哥夫斯基线圈通常用于测量高频电流或大电流,测量环境具有较大的电磁干扰,测量时需要特别注意。为了减小干扰的影响,优先选用数字量输出的积分器。
数字量输出积分器在积分器内部即完成了罗哥夫斯基线圈输出电压信号的积分及AD采样,并将AD采样结果以光纤为介质上传至二次仪表或上位机。可以有效避免传输过程中的损耗及干扰。使用时注意积分器与罗哥夫斯基线圈的模拟量连线尽可能短,并尽量采用屏蔽线。
- 相关百科
- 相关知识
- 相关专栏
- 积存金
- 积木堆式住宅
- 积木家
- 积木家装饰装修工程(天津)有限公司
- 积极安全管理视域下的煤矿安全管理制度有效性研究
- 积水(上海)国际贸易有限公司
- 积水
- 积载因数
- 称重式食用油灌装机
- 称重给煤机
- 秸秆发电厂设计规范(GB50762-2012)
- 秸秆发电经济性与环境影响评价研究
- 秸秆循环利用
- 秸秆沼气工程工艺设计规范
- 秸秆沼气
- 秸秆综合利用100问
- 张力式电子围栏周界防范报警系统设计原理及应用现状
- 流体输送机械化工原理
- 工程结构混凝土结构设计原理模拟试卷一含答案收集资料
- 基于LVDT测量原理活塞式压力计活塞位置指示装置
- 基于平衡计分卡原理
- 旧水泥路面加铺沥青面层设计原理与施工要点分析
- 化工原理、松香施胶剂、木材防腐研讨会
- 基于粒子群优化伺服系统比例积分微分控制器设计方法
- 两岔口隧道新奥法施工过程模拟原理及Ⅲ级围岩施工方法
- 基于最大熵原理与最优化方法隧道衬砌结构可靠度分析
- 基于解耦设计积分分离控制器在协调控制系统中应用
- 江西富士X400-lift同步电梯电气原理图、接线图
- TCL王牌液晶LCD彩电26H机芯模拟板电路原理图
- 混凝土高效膨胀剂的结构自防水原理及其无缝施工技术
- 常见消防设备设施及原理
- 多目标灰色局势决策原理在酪蛋白凝聚工艺参数优化上的应用