静定与超静定问题
静定与超静定问题（statically determinate and statically indeterminate）力系平衡时，未知数（包括未知力的大小、方向或物体的平衡位置）数目与平衡方程的数目相等时，可由静力学平衡方程求出全部未知数，称为静力学可定问题或静定问题。如果未知数数目大于平衡方程数，则不能通过平衡方程解出全部未知数，称为静力学不定问题、静不定问题或超静定问题。
静定与超静定问题基本信息
| 中文名 | 静定与超静定问题 | 外文名 | statically determinate andstatically indeterminate |
|---|
静定与超静定问题（statically determinate andstatically indeterminate）力系平衡时，未知数（包括未知力的大小、方向或物体的平衡位置）数目与平衡方程的数目相等时，可由静力学平衡方程求出全部未知数，称为静力学可定问题或静定问题。如果未知数数目大于平衡方程数，则不能通过平衡方程解出全部未知数，称为静力学不定问题、静不定问题或超静定问题。
求解超静定问题需要用到材料力学知识。
静定与超静定问题造价信息
静定与超静定问题常见问题
-
区别在于约束个数，材料力学里，一般固定端约束为三次约束，一个固定铰支座为一次约束，一个活动铰支座为一次约束。相对一个杆件而言，三个约束就足够保持平衡，称为静定结构。而超过了三个约束，就称为超静定。当约...
-
简单的定义就是，静定结构的自由度数量和约束数量相等，超静定结构是约束数量大于自由度数量。也就是说，静定结构只要有一个约束出现故障失效，那么整个结构就成为可变结构了。而超静定有多余的约束，个别约束失效了...
-
从几何构造分析的角度看，结构必须是几何不变体系。根据多余约束 n ，几何不变体系又分为： 有多余约束( n > 0)的几何不变体系——超静定结构； 无多余约束( n = 0)的几何不变体系——静...
静定与超静定问题文献
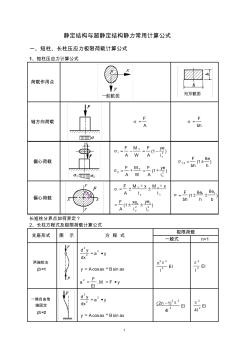静定结构与超静定结构静力计算公式
1 静定结构与超静定结构静力常用计算公式 一、短柱、长柱压应力极限荷载计算公式 1、短柱压应力计算公式 荷载作用点 轴方向荷载 A F bh F 偏心荷载 )1( 21 x Y i ye A F W M A F )1( 22 x Y i ye A F W M A F ) 6 1(2,1 h e bh F 偏心荷载 )1( 22 x y y x x x y Y i ye i xe A F I xM I xM A F ) 66 1( b e h e bh F yx 长短柱分界点如何界定？ 2、长柱方程式及极限荷载计算公式 支座形式 图 示 方 程 式 极限荷载 一般式 n=1 两端铰支 β=1 ya dx yd 2 2 2 axBaxAy sincos yFM EI F a ,2 EI l n 2 22 EI l 2 2 一端自由他 端固定 β=2 ya dx yd 2 2 2 axB
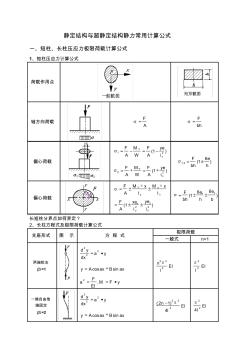1、静定结构与超静定结构静力计算公式
静定结构与超静定结构静力常用计算公式 一、短柱、长柱压应力极限荷载计算公式 1、短柱压应力计算公式 荷载作用点 轴方向荷载 A F bh F 偏心荷载 )1( 21 x Y i ye A F W M A F )1( 22 x Y i ye A F W M A F ) 6 1(2,1 h e bh F 偏心荷载 )1( 22 x y y x x x y Y i ye i xe A F I xM I xM A F ) 66 1( b e h e bh F yx 长短柱分界点如何界定？ 2、长柱方程式及极限荷载计算公式 支座形式 图 示 方 程 式 极限荷载 一般式 n=1 两端铰支 β=1 ya dx yd 2 2 2 axBaxAy sincos yFM EI F a ,2 EI l n 2 22 EI l 2 2 一端自由他 端固定 β=2 ya dx yd 2 2 2 axBaxA
钱令希等的《超静定与静定结构学》分两卷，分别包括《超静定结构学》与《静定结构学》两本书的内容。上卷内容包括：绪论；结构形变；超静定结构一般性分析法；连续梁与刚构；刚构房屋之分析；桁架次应力；柱比法及变梁常数；拱；连续拱；空腹桁架；余能理论。下卷内容包括：总论；结构稳定性的研究；静定梁结构；静定桁架结构；静定拱型结构；静定立体桁架结构。
《超静定与静定结构学》可供工程设计和科学研究人员使用，也可供有关高等院校师生参考。
首先判断其外超静定次数，再判断内超静定次数，二者之和为系统的总超静定次数。
钱令希等的《超静定与静定结构学》这本书是写给土木工程系和水利工程系大学三四年级同学读的，可以作为新学程中结构学(二)和(三)的教材。
本书的内容，竭力想做到精简和带有启发性。在简短的篇幅中，想有系统的介绍一条大道给读者可以迈步前进。在教学中，常有这样的现象，就是依据一本或几本厚厚的西文书，在有限的学期中，只能挑拣几章来教，有些材料太哕唆，有些问题却又永远没有机会理会，不免有些断章取义的弊病，那些书可能写得很好，只是材料没有处理得当，没有显著的重心，这样在教学上就一定减低了效率。
静定与超静定问题相关推荐
- 相关百科
- 相关知识
- 相关专栏
- 静定梁
- 静定问题
- 静态工作点
- 静态总投资
- 静态投资回收期
- 静态热重分析法
- 静态爆破
- 静怡轩
- 静怡轩木器钟表书籍路设陈设帐
- 静摩擦系数表
- 静止同步串联补偿装置
- 静止同步补偿器(STATCON)
- 静止无功功率补偿技术
- 静水压
- 静水压休克
- 静水压强
- 引嫩工程扩建区土壤水盐动态与防治土壤盐碱措施
- 中国工程图学学会成立工程与制造系统集成化分会
- 影响萘高效减水剂与普通硅酸盐水泥适应性的关键因素
- 智能建筑工程报警与电视监控系统前端设备的安装施工
- 应对水源突发污染的城市供水应急处理技术与应用
- 宜兴沈北路二号桥大直径钻孔灌注桩的施工与质量控制
- 招远电视台制作播出系统数字化改造工程的设计与实践
- 正压送风对降低污水厂设备腐蚀的作用与实践(论文)
- 云南郝家河砂岩型铜矿床地质特征与接替资源勘查成果
- 政府与社会资本合作(PPP)项目审计监督理论
- 应用清单招标与经评审的最低投标价法评标的几点思考
- 智能化技术在电气工程自动化控制中的应用与实践研讨
- 中国电动汽车充电站市场现状与投资分析报告
- 智能小区以太接入交换机SNMP代理设计与实现
- 智能建筑虚拟仪器监控系统与控制网络的接口技术
- 有色金属技术经济院与广亚铝业签署战略合作协议
最新词条
安徽省政采项目管理咨询有限公司
数字景枫科技发展（南京）有限公司
怀化市人民政府电子政务管理办公室
河北省高速公路京德临时筹建处
中石化华东石油工程有限公司工程技术分公司
手持无线POS机
广东合正采购招标有限公司
上海城建信息科技有限公司
甘肃鑫禾国际招标有限公司
烧结金属材料
齿轮计量泵
广州采阳招标代理有限公司河源分公司
高铝碳化硅砖
博洛尼智能科技（青岛）有限公司
烧结刚玉砖
深圳市东海国际招标有限公司
搭建香蕉育苗大棚
SF计量单位
福建省中亿通招标咨询有限公司
泛海三江
威海鼠尾草
广东国咨招标有限公司
Excel 数据处理与分析应用大全
甘肃中泰博瑞工程项目管理咨询有限公司
拆边机
山东创盈项目管理有限公司
当代建筑大师
广西北缆电缆有限公司
大山槟榔
上海地铁维护保障有限公司通号分公司
舌花雏菊
甘肃中维国际招标有限公司
华润燃气（上海）有限公司
湖北鑫宇阳光工程咨询有限公司
GB8163标准无缝钢管
中国石油炼化工程建设项目部
韶关市优采招标代理有限公司
莎草目
电梯平层准确度
建设部关于开展城市规划动态监测工作的通知
广州利好来电气有限公司
苏州弘创招投标代理有限公司