节点分析法基本描述
在电路分析里,节点分析(nodal analysis)是一种用电路的节点电压来分析电路的一种方法。
节点分析与网目分析是分析电路所使用的两种主要方法。基尔霍夫电流定律与基尔霍夫电压定律分别是节点分析与网目分析的基础理论。根据基尔霍夫电流定律,节点分析会对于每一节点给出一个方程式,要求所有进入某节点的支路电流的总和等于所有离开这节点的支路电流的总和,而支路电流则表示为节点电压的线性函数。注意到每一条支路的本构关系(constitutive relation)必须给出支路电流与节点电压之间的线性函数关系,称为“导纳表现”。假设每一条支路的本构关系都有导纳表现,则可以做节点分析。例如,对于电阻为
对于任意电路,节点分析会给出一组简洁的方程式,假若不庞大,可以手工解析,或著可以应用线性代数理论,然后使用电脑计算结果。由于节点分析给出的联立方程式相当简洁,很多电路模拟程式(例如,集成电路模拟程式)以节点分析为基础。假若某支路的本构关系不具有导纳表现,则可以将节点分析延伸,使用修正节点分析(modified nodal analysis)。
对于简单的线性元件案例,使用节点分析方法解析相当容易。对于比较复杂的非线性电路,也可以使用节点分析,只要应用牛顿法,将非线性问题改变为一个序列的线性问题。
节点分析法造价信息
-
标出电路里所有相连接的导线,设定每一群相连接的导线为单独节点。在相邻的两个结点之间,必定有一个元件。
-
选择一个节点为参考点。设定这参考点为接地点,电位为零,以接地线或底架标示于电路图。这选择不会影响结果,但可以简化运算。通常,选择连接最多支路的节点可以使解析更加简易。
-
对于每一个未知电压节点,按照基尔霍夫电流定律,写出一个方程式,要求所有流入这节点的支路电流的总和等于所有流出这节点的支路电流的总和。特别注意,节点的电压指的是节点与参考点之间的电压差。
-
假若有电压源处于两个未知电压节点之间,则可合并这两个节点为单独一个“超节点”(supernode),将进入与离开这两个节点的电流一同按照基尔霍夫电流定律处理。另外,再添加一个电压方程式,写出这两个节点的电压关系。
-
解析这一组联立方程式,寻求每一个未知电压。
节点分析法基本案例
如图1所示,
通过电阻器
通过电阻器
通过电流源
应用基尔霍夫电流定律,
节点分析法超节点案例
如图2所示,
注意到通过电压源
节点分析法基本描述常见问题
节点分析法基本描述文献

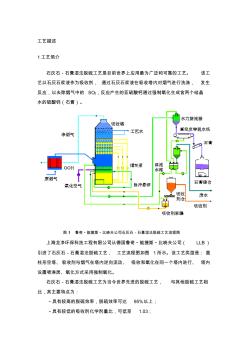 湿法工艺描述
湿法工艺描述
工艺描述 1工艺简介 石灰石-石膏湿法脱硫工艺是目前世界上应用最为广泛和可靠的工艺。 该工 艺以石灰石浆液作为吸收剂, 通过石灰石浆液在吸收塔内对烟气进行洗涤, 发生 反应,以去除烟气中的 SO2,反应产生的亚硫酸钙通过强制氧化生成含两个结晶 水的硫酸钙(石膏)。 图 1 鲁奇·能捷斯·比晓夫公司石灰石-石膏湿法脱硫工艺流程图 上海龙净环保科技工程有限公司从德国鲁奇·能捷斯·比晓夫公司( LLB) 引进了石灰石-石膏湿法脱硫工艺, 工艺流程图如图 1所示。该工艺类型是: 圆 柱形空塔、吸收剂与烟气在塔内逆向流动、 吸收和氧化在同一个塔内进行、 塔内 设置喷淋层、氧化方式采用强制氧化。 石灰石-石膏湿法脱硫工艺为当今世界先进的脱硫工艺, 与其他脱硫工艺相 比,其主要特点为: ·具有较高的脱硫效率,脱硫效率可达 95%以上; ·具有较低的吸收剂化学剂量比,可低至 1.03; ·较大幅度降低了液

 岗位描述范文
岗位描述范文
岗位描述范文 文秘岗位描述文 秘 岗 位 描 述尊敬的各位领导:大家好!我叫 XXX,在医院办公室从事文秘工作。 医院办公室工作综合性强,职能多样,承担着上情下达、会议组 织、职工体检、后勤保障、网络维护等职责,下面我介绍下自己的岗 位职责:一、岗位职责: 1、听从办公室主任的领导,完成各项工作任 务,协助办公室主任做好日常行政事务; 2、负责医院各类公文、 总结、 请示、汇报等文字材料的撰写及上报工作; 3、责医院文件档案的收集、 整理、保管、统计、清理和提阅,归档工作;对归档文件,以件为单 位进行系统、科学地分类整理,以年度为单位排序、存放,方便领导 及时调取。 4、协助、筹备医院重大活动和会务安排。 全面而细致的做好会前准备工作和会后的整理工作,为会议的顺 利进行提供全力保障。 5、接听电话,做好记录。 需要转达时要认真记录对方的身份和要转达的内容,根据具体情 况,清楚、准确、迅速地
节点分析法基本案例
如图1所示,
通过电阻器
通过电阻器
通过电流源
应用基尔霍夫电流定律,
节点分析法超节点案例
如图2所示,
注意到通过电压源
在电路分析里,节点分析(nodal analysis)是一种用电路的节点电压来分析电路的一种方法。
节点分析与网目分析是分析电路所使用的两种主要方法。基尔霍夫电流定律与基尔霍夫电压定律分别是节点分析与网目分析的基础理论。根据基尔霍夫电流定律,节点分析会对于每一节点给出一个方程式,要求所有进入某节点的支路电流的总和等于所有离开这节点的支路电流的总和,而支路电流则表示为节点电压的线性函数。注意到每一条支路的本构关系(constitutive relation)必须给出支路电流与节点电压之间的线性函数关系,称为“导纳表现”。假设每一条支路的本构关系都有导纳表现,则可以做节点分析。例如,对于电阻为
对于任意电路,节点分析会给出一组简洁的方程式,假若不庞大,可以手工解析,或著可以应用线性代数理论,然后使用电脑计算结果。由于节点分析给出的联立方程式相当简洁,很多电路模拟程式(例如,集成电路模拟程式)以节点分析为基础。假若某支路的本构关系不具有导纳表现,则可以将节点分析延伸,使用修正节点分析(modified nodal analysis)。
对于简单的线性元件案例,使用节点分析方法解析相当容易。对于比较复杂的非线性电路,也可以使用节点分析,只要应用牛顿法,将非线性问题改变为一个序列的线性问题。
-
标出电路里所有相连接的导线,设定每一群相连接的导线为单独节点。在相邻的两个结点之间,必定有一个元件。
-
选择一个节点为参考点。设定这参考点为接地点,电位为零,以接地线或底架标示于电路图。这选择不会影响结果,但可以简化运算。通常,选择连接最多支路的节点可以使解析更加简易。
-
对于每一个未知电压节点,按照基尔霍夫电流定律,写出一个方程式,要求所有流入这节点的支路电流的总和等于所有流出这节点的支路电流的总和。特别注意,节点的电压指的是节点与参考点之间的电压差。
-
假若有电压源处于两个未知电压节点之间,则可合并这两个节点为单独一个“超节点”(supernode),将进入与离开这两个节点的电流一同按照基尔霍夫电流定律处理。另外,再添加一个电压方程式,写出这两个节点的电压关系。
-
解析这一组联立方程式,寻求每一个未知电压。
- 相关百科
- 相关知识
- 相关专栏
- 节煤机械
- 节煤设备
- 节煤降烟剂
- 节电饮水台
- 节肢选煤筛
- 节能发电机
- 节能家电
- 节能防灾型钢管混凝土结构
- 节能高效格子型球磨机中空轴
- 芜湖三颐照明有限公司
- 芜湖东旭光电科技有限公司
- 芜湖久源电缆材料有限公司
- 芜湖亿科玻璃制品有限公司
- 芜湖众悦门窗有限公司
- 芜湖众钧广告有限责任公司
- 芜湖佳宏新材料有限公司
- 影响方管柱H型钢梁隔板贯通式节点承载力的参数分析
- 异形柱框架及短肢墙抗震节点构造的施工质量保证措施
- 执行新颁公路基本建设概、预算编制办法及定额的体会
- 在全国抗旱和农田水利基本建设电视电话会议上的讲话
- 圆钢管混凝土T型焊接节点应力强度因子计算方法
- 圆钢管KK型搭接节点内隐藏焊缝焊接与否有限元分析
- 圆钢管混凝土K型焊接管板节点试验和有限元分析
- 张金如厅长在全省农田水利基本建设工作会议上的讲话
- 应急救援预案编制的基本步骤与应急演练工作计划汇编
- 制作质量对塔式起重机结构件焊接节点疲劳性能的影响
- 中国内地房地产投资信托基金的定位、模式及基本框架
- 基于CC1010芯片的无线传感器网络节点设计
- 公路建设监督管理办法基本建设程序监督管理
- 关于基本建设、更新改造、大修工程施工实施改革
- 工程咨询继续教育公路建设项目基本建设程序试卷
- 公路造价师考试基础理论及法规公路基本建设程序试题