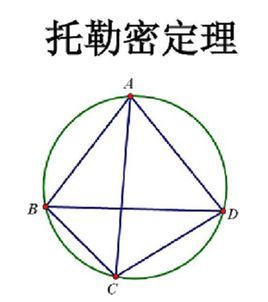
广义托勒密定理

托勒密(Ptolemy)定理指出，圆内接凸四边形两对对边乘积的和等于两条对角线的乘积，其推论是任意凸四边形ABCD，必有AC·BD≤AB·CD+AD·BC，而且当ABCD四点共圆时取等号。

广义托勒密定理概述
广义托勒密定理造价信息
广义托勒密定理常见问题
广义托勒密定理文献

广义托勒密定理图片

广义托勒密定理基本信息

中文名称	广义托勒密定理	外文名称	Ptolemy
内容	凸四边形对边乘积和≥对角线的积	提出者	托勒密

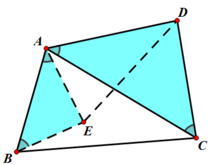
广义托勒密定理概述

托勒密定理的推论:任意凸四边形ABCD，必有AC·BD≤AB·CD+AD·BC，而且当ABCD四点共圆时取等号。

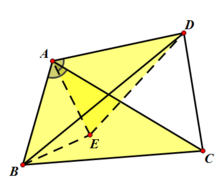
证明如下:在四边形ABCD中,连接AC、BD,作∠ABE=∠ACD,∠BAE=∠CAD

则△ABE∽△ACD

∴ BE/CD=AB/AC,AB/AC=AE/AD

∴BE*AC=AB*CD ①,AB/AE=AC/AD

∵∠BAE=∠CAD

∴∠BAE+∠EAC=∠CAD+∠EAC

即∠BAC=∠DAE

又∵AB/AE=AC/AD,

∴△ABC∽△AED

∴BC/ED=AC/AD

∴ED*AC=AD*BC②

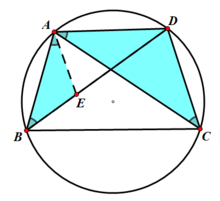
①+②,得

AC*(BE+ED)=AB*CD+AD*BC

又∵BE+ED≥BD

∴AC*BD≤AB*CD+AD*BC

从而命题得证，

且仅当E点落在线段BD上时，等号成立

此时∠ABD=∠ACD

∴ABCD四点共圆

查看详情

广义托勒密定理造价信息

市场价

信息价

询价

材料名称	规格/型号	市场价（除税）	工程建议价（除税）	品牌	单位	税率	供应商
勒杜鹃	株高150-180cm,冠幅100-130cm	查看价格	查看价格	韶顺然花木场	株	13%	佛山市顺德区北滘镇韶顺然花木场
勒杜鹃	勒杜鹃;紫花桩景造型勒杜鹃;桩景造型头径8-10cm 自然高×冠幅200-250cm×150-180cm 造型支数8片栽培方式容器苗	查看价格	查看价格	绿态	株	13%	深圳市宸洲环保科技有限公司
勒杜鹃	勒杜鹃;紫花球型勒杜鹃;球形造型,钢丝焊接1.6米园型,树枝围钢丝编织球形修剪,自然高×冠幅:160cm×160cm土球直径:40cm	查看价格	查看价格	绿态	株	13%	深圳市宸洲环保科技有限公司
三角托架	1600A	查看价格	查看价格	众联兴	副	13%	众联兴电力科技有限公司
红色勒杜鹃	红色勒杜鹃;自然高×冠幅:200-250cm×120-150cm;植物形状:自然形;土球直径:50cm	查看价格	查看价格	绿态	株	13%	深圳市宸洲环保科技有限公司
造型勒杜鹃	勒杜鹃;紫花桩景造型勒杜鹃;桩景造型头径10-15cm 自然高×冠幅250-300cm×200-250cm 造型支数12片栽培方式容器苗	查看价格	查看价格	绿态	株	13%	深圳市宸洲环保科技有限公司
红色勒杜鹃	红色勒杜鹃;红色自然形勒杜鹃; 头径13-15cm 自然高×冠幅220-250cm×150-180cm枝条饱满	查看价格	查看价格	绿态	株	13%	深圳市宸洲环保科技有限公司
勒杜鹃(红色）	230#精品苗自然高×冠幅:40-50cm×30-35cm 土球直径:23cm	查看价格	查看价格	绿态	盆	13%	深圳市宸洲环保科技有限公司

材料名称	规格/型号	除税信息价	含税信息价	行情	品牌	单位	税率	地区/时间
暂无数据

材料名称	规格/需求量	报价数	最新报价（元）	供应商	报价地区	最新报价时间
勾股定理	1200×800×1200\|1项	3	查看价格	安徽盛鸿展览工程有限公司	全国	2022-09-21
四色定理	1200×800×1200\|1项	3	查看价格	安徽盛鸿展览工程有限公司	全国	2022-09-21
数学原理组	制作原型转盘,转盘内按照数学定理设计不同形状液体容器和管道,观众旋转转盘,通过观察其中定量液体形态及珠子走向形态等变化,了解勾股定理、圆锥与圆柱以及概率的数学原理\|1项	1	查看价格	安徽盛鸿展览工程有限公司	全国	2022-08-15
数学原理组	制作原型转盘,转盘内按照数学定理设计不同形状液体容器和管道,观众旋转转盘,通过观察其中定量液体形态及珠子走向形态等变化,了解勾股定理、圆锥与圆柱以及概率的数学原理\|1项	1	查看价格	合肥金诺数码科技股份有限公司	全国	2022-09-14
数学原理组	制作原型转盘,转盘内按照数学定理设计不同形状液体容器和管道,观众旋转转盘,通过观察其中定量液体形态及珠子走向形态等变化,了解勾股定理、圆锥与圆柱以及概率的数学原理\|1项	1	查看价格	鸿瑞工美(深圳)实业有限公司	全国	2022-10-24
数学原理组	制作原型转盘,转盘内按照数学定理设计不同形状液体容器和管道,观众旋转转盘,通过观察其中定量液体形态及珠子走向形态等变化,了解勾股定理、圆锥与圆柱以及概率的数学原理\|1项	1	查看价格	安徽东一特电子技术有限公司	全国	2022-09-16
自动扶梯	FT-1、2、广义梯级宽度1000mm、提升高度5100m、倾斜角度30°、额定速度0.5m/s、理论输送能力(人/小时)9000、1F-2F\|2部	6	查看价格	东莞市富士电梯有限公司		2015-12-08
自动扶梯	FT-1-4、广义梯级宽度1000mm、提升高度5600m,5400m、倾斜角度30°、额定速度0.5m/s、理论输送能力(人/小时)9000、1F-3F\|4部	6	查看价格	东莞市富士电梯有限公司		2015-12-08

广义托勒密定理常见问题

勾股定理怎么算？

80*80+50*50后开方。
斜切角定理如何证明？

首先更正一下，是弦切角，老沈瞎说呢。你把图画出来,AB是圆O切线，AC是弦。做过切点A的直径，交圆O于A、D。连接B、D。证明：因为AD是圆O直径，AB是圆O切线所以∠C=90°=∠BAD所以∠BAC...
圆切角定理是什么?

没有圆切角定理，只有弦切角定理：弦切角等于它所夹的弧对的圆周角