高效范本:石膏几何体
《高效范本:石膏几何体》内容简介:我们在运用边临摹边写生的学习方法之前,要对写生对象的体面关系进行全方位的观察,上下、左右、前后地进行反复研究,看不清楚的地方甚至可以用手触摸感知,这样能加深自己对对象的形体结构的理解,使自己在下笔之前做到心中有数。
高效范本:石膏几何体基本信息
| 书名 | 高效范本 | 出版社 | 浙江人民美术出版社 |
|---|---|---|---|
| 页数 | 48页 | 开本 | 8 |
| 品牌 | 浙江人民美术出版社 | 作者 | 林双双 |
| 出版日期 | 2010年6月1日 | 语种 | 简体中文 |
| ISBN | 9787534028854 | ||
高效范本:石膏几何体造价信息
高效范本:石膏几何体常见问题
-
石膏几何体有不同的分类,所以价格也是不一样的,被用来当画画的模板来使用的价格不是很高,每个售价在50元左右,如果是石膏几何体的装饰品,价格稍微高一点,每个售价在150元左右。以上价格来源于网络,仅供参...
-
不知道
-
你好!很高兴为你解答,有在网上帮你查阅相关资料请你参考:花盆的种类很多,就列举个比较常见的花盆几何体吧!圆台因上下粗细同差多啦初单元应该还没学圆台
高效范本:石膏几何体文献

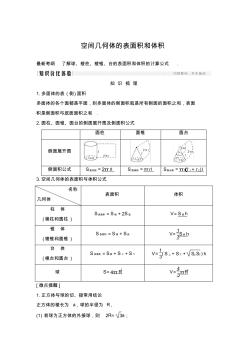 空间几何体的表面积和体积
空间几何体的表面积和体积
空间几何体的表面积和体积 最新考纲 了解球、棱柱、棱锥、台的表面积和体积的计算公式 . 知 识 梳 理 1.多面体的表 (侧)面积 多面体的各个面都是平面,则多面体的侧面积就是所有侧面的面积之和,表面 积是侧面积与底面面积之和 . 2.圆柱、圆锥、圆台的侧面展开图及侧面积公式 圆柱 圆锥 圆台 侧面展开图 侧面积公式 S圆柱侧=2π rl S 圆锥侧=π rl S圆台侧=π(r 1+ r 2) l 3.空间几何体的表面积与体积公式 名称 几何体 表面积 体积 柱 体 (棱柱和圆柱 ) S表面积=S 侧+2S 底 V=S 底h 锥 体 (棱锥和圆锥 ) S 表面积=S 侧+S底 V= 1 3S底 h 台 体 (棱台和圆台 ) S 表面积=S侧+S 上+S 下 V= 1 3( S 上+S下+ S上S下) h 球 S=4π R 2 V= 4 3πR 3 [微点提醒 ] 1.正方体与球的切、

 运用『木板钻孔』原理构建高效几何教学
运用『木板钻孔』原理构建高效几何教学
几何证明题是培养学生逻辑思维能力的一种数学题型,是在中考数学试题中必不可少的一种考查题型。南于这种题型方便考查学生数学基础知识、数学逻辑思维以及创新思维能力,所以,一直是中考命题者的“最爱”。正是南于年年都考,年年都有创新,以至于几何证明题在中考试卷中成为了重点和难点,成为闲扰学生的一大难题。一线的中学数学教师们对该题型的探索和研究一直没有停止。

前段时间在高三教学中遇到这样的问题:
在高考立体几何考点中涉及到空间几何体的截面的地方较多, 如:判断截面的形状、计算出空间几何体的截面周长或面积、或者求与之相关的体积问题、以及最值问题都在考察之列,但是要顺利地解决前面所提到的诸多问题,都必须首先掌握空间几何体截面的作图。
在立体几何中,把空间问题转化为平面问题,历来是立体几何的一个基本问题。而已知不共线三点,作几何体的截面,既是转化为平面问题的一个方法,也是深化理解空间点线面关系的一个很好的途径。
作几何体的截面,是立休几何教学中的一个难点,需要较强的空间想象能力和动手操作能力,正确判断几何体被一个平面所截的截面形状,关键在于弄清这个平面与几何体的面相交成线的形状和位置。让学生掌握作几伺体截面的方法,有助于深入理解直线和平面的有关性质,有效地形成空间概念。
一个平面截一个几何体,这个平面和几伺体的各个面交线,围成一个封闭的平面图形,这个封闭图形就称为几何体的截面。如果几何体是多面体,其截面是多面形;如果几何体是旋转体,其截面还可能是二次曲线所围成的封闭图形。
截面的问题的研究,对于发展学生的空间想象能力,综合运用立体几何各方面的知识技能,提高学生的解题能力,都是十分有启发、思考价值的题材、是立体几何重要的学习目的;而对学生进行空间几何体截面的作图等训练正是培养和发展学生的这一能力,同时也成为了促进学生综合运用空间构图方面知识开发教学兴趣点的拓展课题。
接下来小编从原理和操作两个层面介绍较复杂的不平行于底面的截面问题的解决方案以供参考。
空间几何体的截面的作图主要原理:两个公理及两个性质。
其中,两个公理为:
(1)如果两个不重合的平面有一个公共点,那么它们相交于过此点的一条直线;
(2)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。
两个性质为:
(1)如果一条直线平行于一个平面,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行;
(2)如果两个平面平行,第三个平面和它们相交,那么两条交线平行。
空间几何体的计算要掌握好“定位”、“定形”、“定量”这三个主要的环节。首先,由上面所讲到的方法确定出关键点。其次,由关键点确定截面与空间几何体相关的交线。再次,是根据问题中已知的条件与空间点、线、面的位置关系确定截面的基本特征。最后,运用平面解析几何的有关性质定理与判定定理完成截面相关截面边长、周长、或者面积等数量计算。
空间几何体的截面作图主要的作法:直接法、平行线法、延长法、辅助平面法,接下来,我们依次展开。
一、直接法

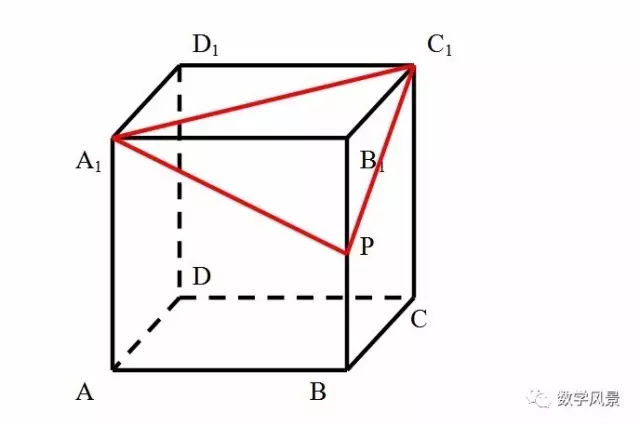
用直接法解决截面问题的关键是:截面上的点在几何体的棱上,且两两在一个平面内,我们可以借助于公理:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内,直接解决这类问题。
二、平行线法

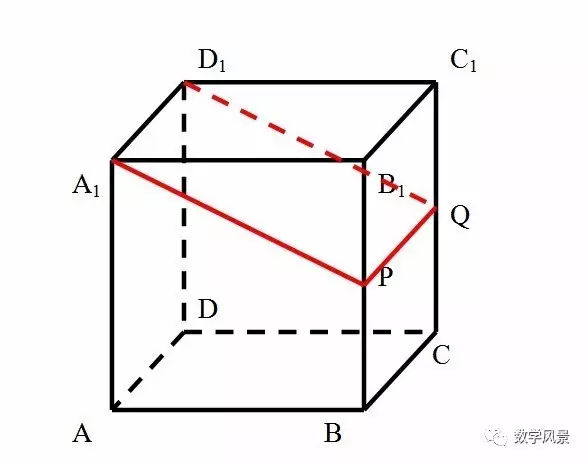
用平行线法解决截面问题的关键是:截面与几何体的两个平行平面相交,或者截面上有一条直线与截面上某点在几何体的某一个表面平行。我们可以借助于两个性质,(1)如果一条直线平行于一个平面,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行;(2)如果两个平面平行,第三个平面和它们相交,那么两条交线平行。直接解决这类问题。
三、延长线法

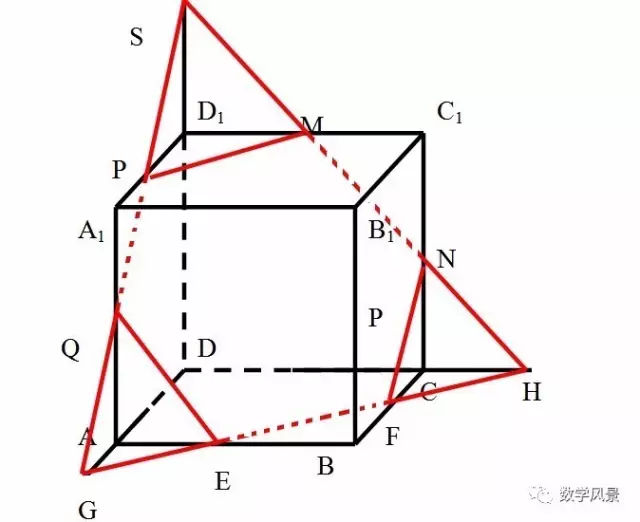
用延长线法解决截面问题的关键是:截面上的点中至少有两个点在一个几何体的一个表面上,我们可以借助于公理,如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。直接解决这类问题。
四、辅助平面法
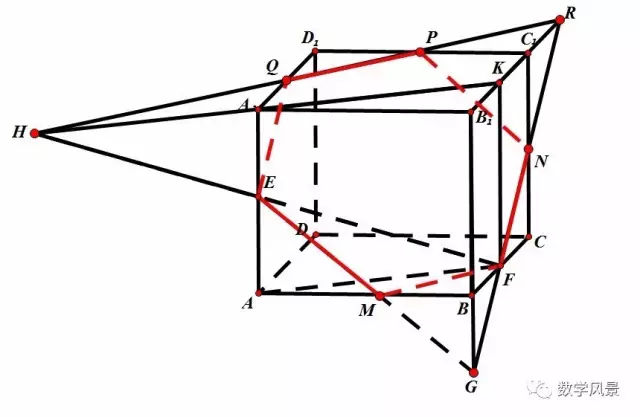

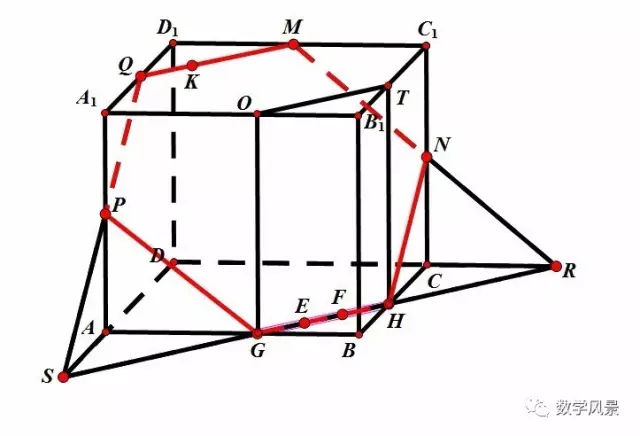

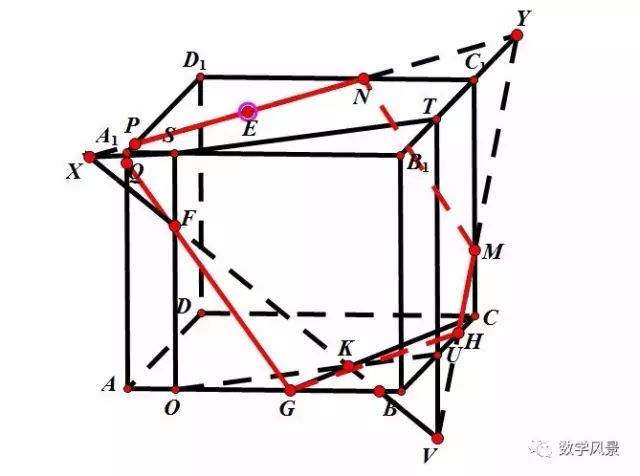

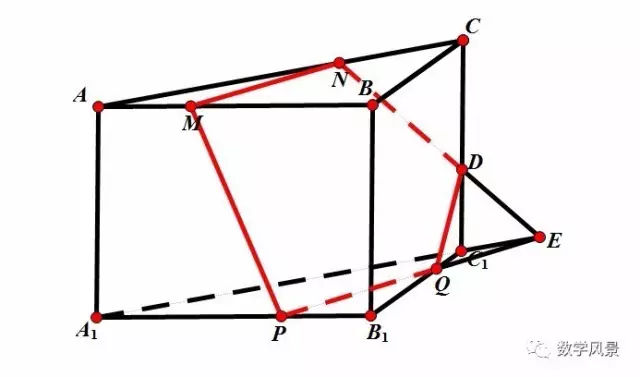
此外,石膏和硬石膏还常呈结核状出现,而这种结核状的硬石膏反映了潮上坪
或沙漠干盐湖的成因特点。 2100433B
教学用的素描教具石膏像,如海盗,大卫,维纳斯,几何体,五官的石膏像。
伟人像类的如毛主席,周恩来,鲁迅等的。
佛像类的如财神,观音,弥勒佛的。
卡通类的有动画人物等。
- 相关百科
- 相关知识
- 相关专栏
- CDL多级离心泵
- 有机肥设备
- 电冰箱检测与修理技能速训
- 双锥混合机(SWMC)
- 注水站
- 帝度BCD-180A
- 灰钙机
- 蠕动泵灌装机
- PVC密封条
- 立式渣浆泵
- 船舶轴功率
- 不锈钢深井潜水泵
- 气体泵
- 大金FVXG272NC-W
- 看图学电冰箱维修300问
- 充油耐震压力表
- 影响萘高效减水剂与普通硅酸盐水泥适应性的关键因素
- 云南省基础设施项目投资建设-回购(BT)合同范本
- 高效率PWM/PFM自动切换升压转换器的设计
- 中国纸面石膏板产业市场现状及投资分析报告
- 政府工程建设领域采购通用招标文件范本
- 应用粉刷石膏解决加气混凝土内墙面粉刷层空鼓和开裂
- 云南省基础设施项目投资建设-回购(BT)合同范本
- 幼儿园及小黄山幼儿园新建项目测绘工程招投标书范本
- 智慧综合执法管理平台建设方案项目招投标书范本
- 脱硫石膏气流煅烧工艺在生产纸面石膏板中的应用
- 新型高效节能的风冷、水淋浴混合冷却式空调机组
- 公安局分局刑侦支队技术室DNA设备公开招投标书范本
- 公路管理局邵家桥服务区及养护站建设工程招投标书范本
- 公路工程管理用表范本预应力钢筋冷拉记录表
- 公路工程管理用表范本索夹制作与防护质量检验报告单
- 工程类投标文件范本
