管制图界限
规格界限:是用以规定质量特性的最大(小)许可值。
上规格界限:USL;下规格界限:LSL; 。
控制界限:是从实际生产出来的产品中抽取一定数量的产品,并进行检测,从所得观测值中计算出来者。
上控制界限:UCL;下控制界限:LCL;
管制图造价信息
管制图按数据性质分类
计量型控制图
平均数与极差控制图( Chart)
平均数与标准差控制图( Chart)
中位数与极差控制图( Chart)
个别值与移动极差控制图( chart)
计数值控制图
不良率控制图(P chart)
不良数控制图(nP chart,又称np chart或d chart)
缺点数控制图(C chart)
单位缺点数控制图(U chart)
管制图用途分类
分析用控制图:根据样本数据计算出控制图的中心线和上、下控制界限,画出控制图,以便分析和判断过程是否处于于稳定状态。如果分析结果显示过程有异常波动时,首先找出原因,采取措施,然后重新抽取样本、测定数据、重新计算控制图界限进行分析。
控制用控制图:经过上述分析证实过程稳定并能满足质量要求,此时的控制图可以用于现场对日常的过程质量进行控制。
SPC管制图是极具有功效的管制工具之一,用以侦测品质变异的原因,然后采取对策以消除其原因,使生产过程恢复正常。
SPC管制图是由三条管制界限,即中心线,上管制界限及下管制界限组成的图形,并将生产过程中所获得的统计量绘入图中,以判定其为管制中抑管制外,如果其状况是属于管制中时,显示生产过程的变异行为掌握在我们的预知中,继续生产.但若其状况是属于管制外,则显示其变异情况已超出我们的控制外,必须控讨其发生的原因,采取对策以矫正之。
管制图定义
控制图是用于分析和控制过程质量的一种方法。控制图是一种带有控制界限的反映过程质量的记录图形,图的纵轴代表产品质量特性值(或由质量特性值获得的某种统计量);横轴代表按时间顺序(自左至右)抽取的各个样本号;图内有中心线(记为CL)、上控制界限(记为UCL)和下控制界限(记为LCL)三条线。
管制图目的
控制图和一般的统计图不同,因其不仅能将数值以曲线表示出来,以观其变异之趋势,且能显示变异属于偶然性或非偶然性,以指示某种现象是否正常,而采取适当的措施。
管制图基本特性
一般控制图纵轴均设定为产品的质量特性,而以过程变化的数据为刻度;横轴则为检测产品的群体代码或编号或年月日等,以时间别或制造先后别,依顺序点绘在图上。
在管制图上有三条笔直的横线,中间的一条为中心线(Central Line,CL),一般用蓝色的实线绘制;在上方的一条称为控制上限(Upper Control Limit,UCL);在下方的称为控制下限(Lower Control Limit,LCL)。对上、下控制界限的绘制,则一般均用红色的虚线表现,以表示可接受的变异范围;至于实际产品质量特性的点连线条则大都用黑色实线绘制。
管制图原理
工序处于稳定状态下,其计量值的分布大致符合正态分布。由正态分布的性质可知:质量数据出现在平均值的正负三个标准偏差(X3)之外的概率仅为0.27%。这是一个很小的概率,根据概率论 “视小概率事件为实际上不可能” 的原理,可以认为:出现在X3区间外的事件是异常波动,它的发生是由于异常原因使其总体的分布偏离了正常位置。
控制限的宽度就是根据这一原理定为3。
管制图分类
管制图也叫控制图,按照分布分为正态分布、用于计量值,二项分布、用于计件值,泊松分布、用于计点值。
表一,分为计量及计数两类,计量管制图可以显现制程上的异常问题,而计数管制图则用於管制整体品质状况好坏。除此之外,可以应用「直方图」了解资料分布情形,或「柏拉图」整理各类主要报废或缺点原因。
常用管制图类别管制图说明
计量值 X Bar – R Chart 平均值与全距管制图
X Bar– S Chart 平均值与标准差管制图
X – Rm Chart 个别值与移动全距管制图
计数值 P Chart 不良率管制图
Pn Chart 不良数管制图
C Chart 缺点数管制图
U Chart 单位缺点数管制图
「管制图」:是实施质量管理作业时,最有效最快速的工具之一,它是美国品管大师博士应用统计数学理论于年所设计的,
它不但能控制制程中质量,且能分析判定制程能力,更可作为新产品设计及制成品验收时的参考。简单说,在
生产过程中,从设计、制造到过程检验三个阶段,皆需用到它,企业如能有效运用此质量知识,便能确保其
在市场上的竞争优势。
管制图界限常见问题
-
规格界限:是用以规定质量特性的最大(小)许可值。上规格界限:USL;下规格界限:LSL; 。控制界限:是从实际生产出来的产品中抽取一定数量的产品,并进行检测,从所得观测值中计算出来者。上控制界限:UC...
-
SPC管制图是极具有功效的管制工具之一,用以侦测品质变异的原因,然后采取对策以消除其原因,使生产过程恢复正常。SPC管制图是由三条管制界限,即中心线,上管制界限及下管制界限组成的图形,并将生产过程中所...
-
1、简易七手法:甘特图、流程图、5W2H、愚巧法、雷达法、统计图、推移图 2、QC旧七大手法:特性要因分析图、柏拉图、查检表、层别法、散布图、直方图、管制图 3、QC新七大手法:关连图、系统图法、KJ...
1.选择质量特性
2.决定管制图之种类
3.决定样本大小,抽样频率和抽样方式
4.收集数据
5.计算管制参数(上,下管制界线等)
6.持续收集数据,利用管制图监视制程
一般构成控制图的要素有:
1. 控制图的数据具有时间先后顺序,不得混乱颠倒,亦即应依取得(生产)的先后顺序排列并绘成图形,亦即一连串的数据为含有时间序列的特性。
2. 控制图上一连串的点子必有波动现象,乃此因变异所引起,变异原因分为两大类,一为机遇原因,一为非机遇原因,非机遇原因引发的大幅度波动现象影响品质较大应避免之,亦即波动现象愈大,品质愈不稳定,管制上下限的宽度将愈宽,此时构成图上点的个别值散布范围亦较大,如与规格比较,较易逸出规格界限外成为不良品。
3. 控制图必须含有统计界限,亦即管制上下限,没有统计的管制上下限不符合控制图原理。通常μ±3σ之管制上限,其横坐标为时间(即组别),纵坐标为品质的刻度。
1.X-R控制图
用于控制对象为长度、重量、强度、纯度、时间、收率和生产量等计量值的场合。X控制图主要用于观察正态分布的均值的变化,R控制图主要用于观察正态分布分散或变异情况的变化,而X-R控制图则将二者联合运用,用于观察正态分布的变化。
2.X-s控制图
与X-R图相似,只是用标准差(s)图代替极差(R)图而已。
3.Me-R控制图
与X-R图也很相似,只是用中位数(Me)图代替均值(X)。
4.X-Rs控制图
多用于对每一个产品都进行检验,采用自动化检查和测量的场合。
5.p控制图
用于控制对象为不合格品率或合格品率等计数质量指标的场合,使用p图时应选择重要的检查项目作为判断不合格品的依据;它用于控制不合格品率、交货延迟率、缺勤率、差错率等。
6.np控制图
用于控制对象为不合格品数的场合。设n为样本,p为不合格品率,则np为不合格品数。
7.c控制图
用于控制一部机器,一个部件,一定长度,一定面积或任何一定的单位中所出现的不合格数目。焊接不良数/误记数/错误数/疵点/故障次数
8.u控制图
当上述一定的单位,也即n保持不变时可以应用c控制图,而当n有变化时则应换算为平均每项单位的不合格数后再使用u控制图。
管制图使用方式
SPC管制图 用于何处?对于所确定的控制对象——统计量应能够定量,这样才能够应用计量控制图;如果只有定性的描述而不能够定量,那就只能应用计数控制图。所控制的过程必须具有重复性,即具有统计规律。
如何选择控制对象?一个过程往往具有各种各样的特性,在使用控制图时应选择能够真正代表过程的主要指标作为控制对象。
怎样选择SPC管制图?选择控制图主要考虑以下几点:首先根据所控制质量特性的数据性质来进行选择,如数据为连续值的应选择X-R图,X-s图,X-Rs图等;数据为计件值的应选择p或np图;数据为计点值的应选择c图或u图。最后,还需要考虑其它要求;如样本抽取及测量的难易和费用高低。
如何分析SPC管制图?如果在控制图中点子未出界,同时点子的排列也是随机的,则认为生产过程处于稳定状态或统计控制状态。如果控制图点子出界或界内点排列非随机,就认为生产过程失控。
注:对于应用控制图的方法还不够熟悉的工作人员来说,即使在控制图点子出界的场合,也首先应该从下列几个方面进行检查:样本的抽取是否随机?测量有无差错?数字的读取是否正确?计算有无错误?描点有无差错?然后再来调查过程方面的原因,经验证明这点十分重要。
对于点子出界或违反其它准则的处理。若点子出界或界内点排列非随机,应立即查明原因并采取措施尽量防止它再次出现。
SPC管制图的重新制定。控制图是根据稳态下的条件(人员、设备、原材料、工艺方法、环境、测量,即5M1E)来制定的。如果上述条件变化,控制图也必须重新加以制定;由于控制图是科学管理生产过程的重要依据,所以经过相当时间的使用后应重新抽取数据,进行计算,加以检验。
计量控制图和计数控制图可分为未给定标准值和给定标准值两种情形,两种情形不能混淆。
SPC管制图的保管问题。控制图属于技术资料,应加以妥善保管,这些资料对于今后在产品设计和制定规范方面都是十分有用的。
管制图风险定义
根据控制限作出的判断也可能产生错误。可能产生的错误有两类。
第一类错误是把正常判为异常,它的概率为,也就是说,工序过程并没有发生异常,只是由于随机的原因引起了数据过大波动,少数数据越出了控制限,使人误将正常判为异常。 虚发警报, 由于徒劳地查找原因并为此采取了相应的措施,从而造成损失. 因此, 第一种错误又称为徒劳错误.
第二类错误是将异常判为正常,它的概率记为,即工序中确实发生了异常,但数据没有越出控制限,没有反映出异常,因而使人将异常误判为正常。漏发警报,过程已经处于不稳定状态, 但并未采取相应的措施,从而不合格品增加, 也造成损失.
两类错误不能同时避免,减少第一类错误(),就会增加第二类错误(),反之亦然。2100433B
管制图界限文献

 门窗制作管制图流程图
门窗制作管制图流程图
门窗制作管制图流程图

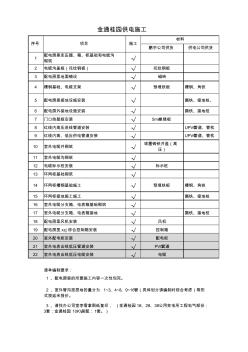 施工范围界限
施工范围界限
鹏宇公司供货 供电公司供货 1 配电房里变压器、箱、柜基础和电缆沟 砌筑 √ 2 电缆沟盖板(花纹钢板) √ 花纹钢板 3 配电房里地面铺设 √ 磁砖 4 槽钢基础、电缆支架 √ 预埋铁板 槽钢、角铁 5 配电房里接地设施安装 √ 扁铁、接地桩、 6 配电房外接地设施安装 √ 扁铁、接地桩 7 门口挡鼠板安装 √ 5mm绝缘板 8 红线内高压进线管道安装 √ UPVC管道、管枕 9 红线内高、低压供电管道安装 √ UPVC管道、管枕 10 室外电缆井砌筑 √ 球墨铸铁井盖(高 压) 11 室外电缆沟砌筑 √ 12 电缆标示桩安装 √ 标示桩 13 环网柜基础砌筑 √ 14 环网柜槽钢基础施工 √ 预埋铁板 槽钢、角铁 15 环网柜接地施工施工 √ 扁铁、接地桩 16 室外电缆分支箱、电表箱基础砌筑 √ 17 室外电缆分支箱、电表箱接地 √ 扁铁、接地桩 18 配电房里风机安装 √ 风机 1
缺点数管制图是一种计数值管制图,能在每一批量的生产中侦测出每一零件或受验单位不良点的数目。
所谓不合格品是指一件物品无法符合一项或多项之规格要求。任何不符合规格之处,称为一个不合格点(nonconformity)或缺点 (defect)。根据不合格点之严重性,我们可能将具有许多不合格点之物品视为合格品。换句话说,具有不合格点之物品,不一定为不合格品。 C管制图是为了管制一个检验单位之总不合格点数。在每一样本中出现不合格点之机率,服从卜瓦松分配的假设下。每个样本出现的缺点数是参数为λ的 Poisson分配,。
【例】:下表是某汽车工厂生产之车门不合格点数记录,每组样本大小为100,试建立管制图。
样组
不合格点数 样组 不合格点数 1 5 14 7
2 8 15 4 3 4 16 9 4 9 17 11 5 12 18 10 6 7 19 6 7 8 20 9 8 12 21 22 9 21 22 13
| 样组 |
不合格点数 |
样组 |
不合格点数 |
| 1 |
5 |
14 |
7 |
| 2 |
8 |
15 |
4 |
| 3 |
4 |
16 |
9 |
| 4 |
9 |
17 |
11 |
| 5 |
12 |
18 |
10 |
| 6 |
7 |
19 |
6 |
| 7 |
8 |
20 |
9 |
| 8 |
12 |
21 |
22 |
| 9 |
21 |
22 |
13 |
因为c管制图在卜瓦松分配的假设下,有几项条件必须符合(Grant和Leavenworth l988,Montgomery 1991):
1.在产品出现不合格点之机会(位置)要相当大,而每一特定位置发生不合格点之机率很小且固定。
2.每一样本发生不合格点之机会(范围)要相同。
3.不合格点之发生需为独立,亦即产品上某一部分发生不合格点不影响其他不合格点之出现。
- 相关百科
- 相关知识
- 相关专栏
- 建设工程定额及概预算(第2版)
- 变形机构图
- 防渗铺盖
- 房产测量规范
- 套管井电阻率测井
- 河南鸿翔市政工程有限公司
- 河南城通市政工程有限公司
- 一图一算之市政工程造价
- 徐州厚鼎土石方工程有限公司
- 电工识图边学边用
- 云南千岩工程质量检测有限公司
- 本质安全型电气设备
- 《渠道》
- 水利行业职业技能培训教材:渠道维护工
- 中发输配电设备有限公司
- 水电站厂房
- 影响工程项目管理中的质量因素与提高质量管理的对策
- 在线解答合同、FIDIC、清单、工程管理问题实况
- 张峰水库2号倒虹预应力钢筒混凝土管道安装施工工艺
- 圆管方管角铝槽铝(20200929163753)
- 医院手术部新风机组盘管冬季冻裂问题分析及防止方法
- 在项目成本控制中的实践与探索工程项目成本管理系统
- 柴油机高压喷油管用钢、高压喷油管及其制造方法
- 永明项目管理有限公司中原分公司中标
- 圆钢管通用规格表(20201009124910)
- 中海地产广州公司精装修工程管理流程之工程管理资料
- 永明项目管理有限公司西宁分公司中标
- 圆CFRP-钢管混凝土轴压短柱荷载-变形关系分析
- 中国哈尔滨国际水处理给排水设备及泵阀管道展会概况
- 中国铁道建筑总公司地下空间安全管理知识培训
- 在建工程评审制度在预拌混凝土生产计划管理中的应用
- 可关断晶闸管(GTO)直接门极驱动电路