高斯线定理基本概念

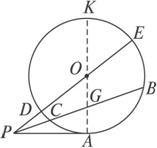
高斯线定理:四边形ABCD中，直线DA与直线CB交于K，直线BA与直线CD交于L，N、M分别为AC、BD的中点，NM交KL与P.则P是KL中点

由共边比例定理知

KP/LP=KMN面积/LMN面积 (1)由定比分点公式的补充公式，得

KMN面积=1/2(KMC面积-KMA面积)

LMN面积=1/2(LMA面积-LMC面积) (2)

由BM=MD=1/2*BD,得

KMC面积=1/2*KDC面积,KMA面积=1/2*KBA面积

LMA面积=1/2*LDA面积,LMC面积=1/2*LBC面积 (3)

(3)代入(2),得

KMN面积=1/4*(KDC面积-KBA面积)=1/4*ABCD面积

LMN面积=1/4*ABCD面积

代入(1),得到KP=LP

作AR,MK,BN平行于LC，AS,DP,LK平行于KC

根据平行四边形对角线的性质S四边形ASRC=S四边形LMAP=S四边形JQAN

∴S四边形JQAP=S四边形LONM

∴A在四边形KMAQ的对角线KA中，A,O,K三点共线

则AC,CO,CK的中点三点共线

则由平行四边形得对角线互相平分所以SR,,BD,KL三点的中点也共线

证毕

1.所谓的平行四边形对角线的性质就是如果过平行四边形对角线的一点分别作两边的平行线，则不含这条对角线的两平行四边形面积相等(如下图)

2.三角形中位线性质:直线AB外有一点P则P与AB线上点的连线的中点都共线

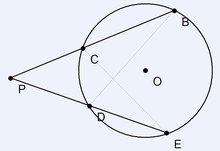
从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等。

从圆外一点P引两条割线与圆分别交于C,B,D,E,则有 PC·PB=PD·PE。如下图所示。 (PA是切线)

Secant Theorem

割线定理为圆幂定理之一(切割线定理推论)，其他二为:

切割线定理

相交弦定理

如图直线PB和PE是自点P引的⊙O的两条割线，则PC·PB=PD·PE.

证明:连接CE、DB

∵∠E和∠B都对弧CD

∴由圆周角定理，得 ∠E=∠B

又∵∠EPC=∠BPD

∴△PCE∽△PDB

∴PC:PD=PE:PB, 也就是PC·PB=PD·PE.

割线定理与相交弦定理，切割线定理通称为圆幂定理。

相交弦定理、切割线定理以及它们的推论统称为圆幂定理。一般用于求线段长度。