割线

人们研究复数域上的解析函数时,常常需要研究函数在整个复平面的性质.然而,有些解析函数定义在复平面上时,表现出多值的性质,这样的函数往往从一个点经过某些曲线回到这个点时,解析变化的函数值会跑到多值中另外的值上面.这样的函数一方面可以采用黎曼曲面作为定义域,使得函数变为单值,另一方面,也可人为地在复平面上画上一条线将复平面合适地割开,使得未被割开的区域内具有单值解析函数的良好性质.这样的人为划出的避免函数解析变化必然出现多值的线就叫割线.

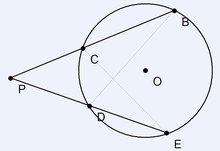
从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等。

从圆外一点P引两条割线与圆分别交于C,B,D,E,则有 PC·PB=PD·PE。如下图所示。 (PA是切线)

Secant Theorem

割线定理为圆幂定理之一(切割线定理推论)，其他二为:

切割线定理

相交弦定理

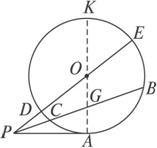
如图直线PB和PE是自点P引的⊙O的两条割线，则PC·PB=PD·PE.

证明:连接CE、DB

∵∠E和∠B都对弧CD

∴由圆周角定理，得 ∠E=∠B

又∵∠EPC=∠BPD

∴△PCE∽△PDB

∴PC:PD=PE:PB, 也就是PC·PB=PD·PE.

割线定理与相交弦定理，切割线定理通称为圆幂定理。

是在由达韦斯·尼古拉所创立的“股票箱理论”的基础上演变而来，并在实用功能上有所扩展。其基本原理、作图方法和研判要点与“股票箱理论”基本相同。

“平行通道分割线”是趋势线和趋势平行线的结合和扩展应用，是分析股价趋势通道的简便工具。 “平行通道分割线”具备了“股票箱”的全部功能与作用，并增设了通道的“分割与扩展”功能。

平行通道分割线作用，主要是用于勾勒出股价波动轨迹之轮廓，以便于直观的观察与判断。用户可以在同一幅K线走势图中，按实战分析的需要划出多种不同的平行通道，并可对其中任意一种平行通道作等分（如，二分之一、三分之一、四分之一等）或任意的分割、扩展。从分析、研判的实际效果来看，该平行通道分割线要比“股票箱”更加符合实战对分析工具的专业要求，尤其是在一个长期的平行通道中，准确细分和清晰界定其中、短期波段的高点和低点，较好的把握该段时间内股价的波动特征和规律，具有较好的指示与帮助作用。

相交弦定理、切割线定理以及它们的推论统称为圆幂定理。一般用于求线段长度。

相交弦定理、切割线定理及割线定理(切割线定理推论)以及他们的推论统称为圆幂定理。一般用于求直线段长度。