非线性转子系统中的传递矩阵技术
《非线性转子系统中的传递矩阵技术》是顾致平编著的一本图书。该书首先介绍了国内外在传递矩阵技术方面的研究进展情况及数学建模基础和数学建模方法现状,然后系统研究了将传递矩阵技术扩展应用于分析非线性转子系统动力响应的方法及传递矩阵技术与等效线性化技术结合的过程。内容阐述简明扼要、深入浅出。
非线性转子系统中的传递矩阵技术基本信息
| 书名 | 非线性转子系统中的传递矩阵技术 | 作者 | 顾致平 |
|---|---|---|---|
| ISBN | 9787030290885 | 定价 | 50.00元 |
| 出版社 | 科学出版社 | 出版时间 | 2010年10月1日 |
| 开本 | 16开 | ||
前言
第1章 绪论
1.1 非线性转子-轴承系统中传递矩阵技术的发展历程
1.2 传递矩阵技术在工程中的应用
参考文献
第2章 传递矩阵技术的数学力学基础
2.1 数学建模方法现状
2.2 传递矩阵技术基础
2.2.1 传递矩阵法原理
2.2.2 典型元件的传递矩阵
2.2.3 轴段的场传递矩阵
2.2.4 集中质量的点传递矩阵
2.2.5 粘弹性支承元件的传递矩阵
2.2.6 轮盘站的传递矩阵
2.3 挤压油膜阻尼器轴承的油膜力模型
2.3.1 挤压油膜阻尼器在航空发动机上的应用
2.3.2 机动飞行对发动机振动的影响
2.3.3 挤压油膜阻尼器工作原理
2.3.4 挤压油膜阻尼器的油膜力
2.3.5 挤压油膜力的非线性特性分析
参考文献
第3章 非线性转子-轴承系统瞬态分析的传递矩阵技术
3.1 Prohl传递矩阵瞬态分析技术
3.1.1 借Newmark差分公式建立传递矩阵
3.1.2 用改进的Prohl传递矩阵法求瞬态响应
3.1.3 改进的Prohl传递矩阵法的数值稳定性分析
3.1.4 例题及讨论
3.2 连续空问离散时间--传递矩阵分析技术
3.2.1 线性转子系统的传递矩阵瞬态分析技术简介
3.2.2 连续空间离散时间--Riccati传递矩阵积分法
3.2.3 计算分析结果
3.3 Riccati传递矩阵瞬态分析技术
3.3.1 Riccati传递矩阵法的改进
3.3.2 新型传递向量{z}j的传递矩阵
3.3.3 方法的数值稳定性分析
3.3.4 例题及分析
参考文献
第4章 非线性转子系统动力响应分析的模态叠加-传递矩阵技术
4.1 轴段场传递矩阵的建立
4.2 非线性转子系统的瞬态分析
4.2.1 方法概述
4.2.2 计算结果分析
参考文献
第5章 非线性转子系统稳态响应分析的传递矩阵一等效线性化技术
5.1 等效线性化--Prohl传递矩阵技术
5.1.1 研究的基本思路
5.1.2 非线性元件的谐波平衡线性化
5.1.3 线性化技术的理论分析
5.1.4 算例及结果分析
5.2 非线性多转子--支承系统的偏置协调响应分析
5.2.1 Riccati传递矩阵法及系统稳态响应的求解
5.2.2 矩阵传递方式分析
5.2.3 例题及计算结果分析
5.3 小结
参考文献
非线性转子系统中的传递矩阵技术造价信息
《非线性转子系统中的传递矩阵技术》适用于电力、机械、航空、宇航、石化、纺织、采矿、交通等工程部门的科技人员,以及有关专业的研究生和本科生。
非线性转子系统中的传递矩阵技术常见问题
-
定理里只有,主对角线,下三角,上三角三种形式的分块矩阵。没有反对角线的,不要靠猜测强行造个定理然后问为什么不对。这种反对角线型的,是可以可以通过列交换变成主对角线型的的。
-
非线性负载是指内含整流设备的负载。在电子线路中,电压与电流不成线性关系,在负载的投入、运行过程中,电压和电流的关系是经常变化的。所谓非线性,就是自变量和变量之间不成线性关系,成曲线或者其他关系。用函数...
-
举例说明a=‘2 3 4 5’;b=str2num(a);结果:b= 2 3 4 5把uitable变成N行一列,用reshape(uitable,N,1); 不过这时N等于uitalbe的数组元素个...
非线性转子系统中的传递矩阵技术文献

 某舰用燃机高压涡轮压气机转子传递矩阵建模
某舰用燃机高压涡轮压气机转子传递矩阵建模
利用有限元法推导某舰用燃气轮机高压涡轮压气机转子的传递矩阵,并建立转子的多体系统传递矩阵模型。通过算例证明,该方法计算准确,为用有限元法和多体系统传递矩阵法求解燃气轮机转子学问题提供了新思路。
内 容 简 介
传递矩阵法是用于工程结构的静态、动态及稳定性分析的一种简便计
算方法。它具有精确度高,力学概念清晰,编制程序容易,适于微机解大题的
优点。
本书详尽地介绍了传递矩阵法的原理及各种传递矩阵的推导过程,阐
述了编制程序的思路,并以大量的算例说明了传递矩阵法在工程上的应用。
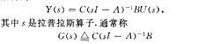
传递函数矩阵概述
传递函数矩阵(transfer function matrix)线性定常系统的一种频域描述方法.给定线性定常系统}(A,B,C).设x(0) = 0,如果记状态x(t),控制 u(t)和输出y(t)的拉普拉斯变换分别为X(s),U(s) 和Y(s),对状态方程和输出方程两边进行拉氏变换后得到
其中,是拉普拉斯算子.通常称
为系统乏的传递函数矩阵.G (s)是以:的有理分式为元素的mX:矩阵.传递函数矩阵G(s)是线性定常控制系统的另外一种描述方法.它是用频域方法分析和设计控制系统的基础.
传递矩阵方法(transfer matrix)是一种用矩阵来描述多输入多输出的线性系统的输出与输入之间关系的手段和方法。该方法曾被用于成功地解决了二维Ising模型。
- 相关百科
- 相关知识
- 相关专栏
- 玻璃钢坐便器
- 套装叶轮拆装
- 德国VC视频矩阵
- INAPSHE17轴承
- 径流式叶轮机械理论及设计
- FAG24034BS.MB轴承
- 不锈钢耐磨多级泵
- 粉叶轮环藤
- I-1B型不锈钢浓浆泵
- 登高卫浴
- VGA矩阵16进16出
- 双叶轮离心泵
- ZCQF型自吸磁力驱动泵
- 多功能坐便器
- 多功能淋浴房
- 卤素大灯
- 分形DGS单元结构设计及其在微带电路中的应用
- 磷铵技术改造五大磷肥工程的建议
- 预制砌块(砖、石)挡土墙工程砌体施工安全技术交底
- 中国工程图学学会成立工程与制造系统集成化分会
- 以贯穿项目为核心载体的建筑工程技术专业素材库建设
- 云计算技术在城市轨道交通运营指挥管理系统中的应用
- 多逆变器太阳能光伏并网发电系统的组群控制方法
- 支持并行工程和智能CAPP的制造资源建模技术
- 智能建筑工程报警与电视监控系统前端设备的安装施工
- 在“建筑节能与居住舒适”专题技术交流会议上的讲话
- 应对水源突发污染的城市供水应急处理技术与应用
- 新型透水衬砌在南台子一级水电站尾水渠中的尝试
- 有限元法在软土浅埋隧道施工过程的动态模拟中的应用
- 引用公路桥涵施工技术规范JTJ0412000
- 招远电视台制作播出系统数字化改造工程的设计与实践
- 全热回收地源热泵空调机组的系统及工程方案设计