反激式变压器的设计
FLYBACK变压器设计之考量因素
1.储能能力.当变压器工作于CCM方式时,由于出现了直流分量,需加AIR GAP,使磁化曲线向 H 轴倾斜,从而使变压器能承受较大的电流,传递更多的能量.
Ve: 磁芯和气隙的有效体积.
or P = 1/2Lp (Imax2 - Imin2)
式中Imax, Imin -- 为导通周期末,始端相应的电流值.
由于反激式变压器磁芯只工作在第一象限磁滞回线,磁芯在交、直流作用下的B.H效果与AIR GAP大小有密切关联,如图4.在交流电流下气隙对ΔBac无改变效果,但对ΔHac将大大增加,这是有利的一面,可有效地减小CORE的有效磁导率和减少原边绕组的电感.
在直流电流下气隙的加入可使CORE承受更加大的直流电流去产生HDC,而BDC却维持不变,因此在大的直流偏置下可有效地防止磁芯饱和,这对能量的储存与传递都是有利的. 当反激变压器工作于CCM时,有相当大的直流成份,这时就必须有气隙.
外加的伏秒值,匝数和磁芯面积决定了B轴上ΔBac值; 直流的平均电流值,匝数和磁路长度决定了H轴上HDC值的位置. ΔBac对应了ΔHac值的范围.可以看出,气隙大ΔHac就大. 如此,就必须有足够的磁芯气隙来防止饱和状态并平稳直流成分.
反激式变压器设计步骤
例如:输入电压:AC90-264V 输出电压:19V 输出电流:3.16A 输出功率:60W 频率:70K
Step1. 选择CORE材质,确定△B
本例为ADAPTER DESIGN,由于该类型机散热效果差,故选择CORE材质应考量高Bs,低损耗及高μi材质,结合成本考量,在此选用Ferrite Core, 以TDK 之 PC40 or PC44为优选, 对比TDK DATA BOOK, 可知 PC44材质单位密度
相关参数如下: μi = 2400 ± 25% Pvc = 300KW / m2 @100KHZ ,100℃
Bs = 390mT Br = 60mT @ 100℃ Tc = 215℃
为防止X'FMR出现瞬态饱和效应, 此例以低△B设计.
选 △B = 60%Bm, 即△B = 0.6 * (390 - 60) = 198mT ≒0.2 T
Step2确定Core Size和 Type.
1> 求core AP以确定 size
AP= AW*Ae=(Pt*104)/(2ΔB*fs*J*Ku)
= [(60/0.83+60)*104]/(2*0.2*70*103*400*0.2) = 0.59cm4
式中 Pt = Po /η +Po 传递功率;
J : 电流密度 A / cm2 (300~500) ; Ku: 绕组系数 0.2 ~ 0.5 .
2> 形状及规格确定.
形状由外部尺寸,可配合BOBBIN, EMI要求等决定,规格可参考AP值及形状要求而决定, 结合上述原则, 查阅TDK之DATA BOOK,可知RM10, LP32/13, EPC30均可满足上述要求,但RM10和EPC30可用绕线容积均小于LP32/13,在此选用LP32/13 PC44,其参数如下:
Ae = 70.3 mm2 Aw = 125.3mm2 AL = 2630±25% le = 64.0mm
AP = 0.88 cm4 Ve = 4498mm3 Pt = 164W ( forward )
Step3估算临界电流 IOB ( DCM / CCM BOUNDARY )
本例以IL达80% Iomax时为临界点设计变压器.
即 : IOB = 80%*Io(max) = 0.8*3.16 = 2.528 A
Step4求匝数比 n
n = [VIN(min) / (Vo + Vf)] * [Dmax / (1-Dmax)] VIN(min) = 90*√2 - 20 = 107V
= [107 / (19 + 0.6)] *[0.5 / (1- 0.5)]
= 5.5 ≒ 6
匝比 n 可取 5 或 6,在此取 6 以降低铁损,但铜损将有所增加.
CHECK Dmax:
Dmax = n (Vo +Vf) / [VINmin + n (Vo + Vf)]= 6*(19 + 0.6) /[107 + 6*(19 + 0.6)] = 0.52
Step5求CCM / DCM临
ΔISB = 2IOB / (1-Dmax) = 2*2.528 / (1-0.52) = 10.533
Step6计算次级电感 Ls 及原边电感 Lp
Ls = (Vo + Vf)(1-Dmax) * Ts / ΔISB = (19+0.6) * (1-0.52) * (1/70000) / 10=12.76uH
Lp = n*n*Ls = 6*6*12.76 = 459.4 uH ≒ 460
此电感值为临界电感,若需电路工作于CCM,则可增大此值,若需工作于DCM则可适当调小此值.
Step7求CCM时副边峰值电流Δisp
Io(max) = (2ΔIs + ΔISB) * (1- Dmax) / 2 ΔIs = Io(max) / (1-Dmax) - (ΔISB / 2 )
ΔIsp = ΔISB +ΔIs = Io(max) / (1-Dmax) + (ΔISB/2) = 3.16 / (1-0.52) + 10.533 / 2=11.85A
Step8求CCM时原边峰值电流ΔIpp
ΔIpp = ΔIsp / n = 11.85 / 6 = 1.975 A
Step9确定Np、Ns
1> Np
Np = Lp * ΔIpp / (ΔB* Ae) = 460*1.975 / (0.2*70.3) = 64.6 Ts
因计算结果为分数匝,考虑兼顾原、副边绕组匝数取整,使变压器一、二次绕组有相同的安匝值,故调整 Np = 60Ts OR Np = 66Ts
考量在设定匝数比n时,已有铜损增加,为尽量平衡Pfe与Pcu,在此先选 Np = 60 Ts.
2> Ns
Ns = Np / n = 60 / 6 = 10 Ts
3> Nvcc
求每匝伏特数Va Va = (Vo + Vf) / Ns = (19+0.6) / 10 = 1.96 V/Ts
∴ Nvcc = (Vcc + Vf) / Va =(12+1)/1.96=6.6
Step10计算AIR GAP
lg = Np2*μo*Ae / Lp = 602*4*3.14*10-7*70.3 / 0.46 = 0.69 mm
Step11计算线径dw
1> dwp
Awp = Iprms / J Iprms = Po / η / VIN(min) = 60/0.83/107 = 0.676A
Awp = 0.676 / 4 J取4A / mm2 or 5A / mm2
= 0.1 (取Φ0.35mm*2)
2> dws
Aws = Io / J = 3.16 / 4 (Φ1.0 mm)
量可绕性及趋肤效应,采用多线并绕,单线不应大于Φ0.4, Φ0.4之Aw= 0.126mm2, 则 0.79 (即Ns采用Φ0.4 * 6)
3> dwvcc Awvcc = Iv / J = 0.1 /4
上述绕组线径均以4A / mm2之计算,以降低铜损,若结构设计时线包过胖,可适当调整J之取值.
4> 估算铜窗占有率.
0.4Aw ≧Np*rp*π(1/2dwp)2 + Ns*rs*π(1/2dws)2 + Nvcc*rv*π(1/2dwv)2
0.4Aw ≧60*2*3.14*(0.35/2)2+10*6*3.14+(0.4/2)2+7*3.14*(0.18/2)2
≧ 11.54 + 7.54 + 0.178 = 19.26
0.4 * 125.3 = 50.12
50.12 > 19.26 OK
Step12估算损耗、温升
求出各绕组之线长. 求出各绕组之RDC和Rac @100℃ 求各绕组之损耗功率 加总各绕组之功率损耗(求出Total值) 如 : Np = 60Ts , LP32/13BOBBIN绕线平均匝长 4.33cm
则 INP = 60*4.33 = 259.8 cm Ns = 10Ts
则 INS = 10*4.33 = 43.3 cm
Nvcc = 7Ts
则 INvc = 7 * 4.33 = 30.31cm
查线阻表可知 : Φ0.35mm WIRE RDC = 0.00268Ω/cm @ 100℃
Φ0.40mm WIRE RDC = 0.00203 Ω/cm @ 100℃
Φ0.18mm WIRE RDC = 0.0106 Ω/cm @ 100℃
R@100℃ = 1.4*R@20℃
求副边各电流值. 已知Io = 3.16A.
副边平均峰值电流 : Ispa = Io / (1-Dmax ) = 3.16 / (1- 0.52) = 6.583A
副边直流有效电流 : Isrms = √〔(1-Dmax)*I2spa〕 = √(1- 0.52)*6.5832 = 4.56A
副边交流有效电流 : Isac = √(I2srms - Io2) = √(4.562-3.162) = 3.29A
求原边各电流值 :
∵ Np*Ip = Ns*Is
原边平均峰值电流 : Ippa = Ispa / n = 6.58 / 6 = 1.097A
原边直流有效电流 : Iprms = Dmax * Ippa = 1.097 * 0.52 = 0.57A
原边交流有效电流 : Ipac = √D*I2ppa = 1.097*√0.52 = 0.79A
求各绕组交、直流电阻.
原边 : RPDC = ( lNp * 0.00268 ) / 2 = 0.348Ω
Rpac = 1.6RPDC = 0.557Ω
副边 : RSDC = ( lNS*0.00203 ) /6 = 0.0146Ω
Rsac = 1.6RSDC = 0.0243Ω
Vcc绕组 : RDC =30.31*0.0106 = 0.321Ω
计算各绕组交直流损耗:
副边直流损 : PSDC = Io2RSDC = 3.162 * 0.0146 = 0.146W
交流损 : Psac = I2sac*Rsac = 3.292*0.0234 = 0.253W
Total : Ps = 0.146 + 0.253 = 0.399 W
原边直流损 : PPDC = Irms2RPDC = 0.572 * 0.348 = 0.113W
交流损 : Ppac = I2pac*Rpac = 0.792*0.557 = 0.348W
忽略Vcc绕组损耗(因其电流甚小) Total Pp = 0.461W
总的线圈损耗 : Pcu = Pc + Pp = 0.399 + 0.461 = 0.86 W
2> 计算铁损 PFe
查TDK DATA BOOK可知PC44材之△B = 0.2T 时,Pv = 0.025W / cm2
LP32 / 13之Ve = 4.498cm3
PFe = Pv * Ve = 0.025 * 4.498 = 0.112W
Ptotal = Pcu + PFe = 0.6 + 0.112 = 0.972 W 估算温升 △t 依经验公式 △t = 23.5PΣ/√Ap = 23.5 * 0.972 / √0.88 = 24.3 ℃
估算之温升△t小于SPEC,设计OK.
Step13结构设计
查LP32 / 13 BOBBIN之绕线幅宽为 21.8mm.
考量安规距离之沿面距离不小于6.4mm.
为减小LK提高效率,采用三明治结构,其结构如下 :
X'FMR结构 :
Np | #1 | 3.2 / 3.2 | 2 -- A | Φ0.35 * 2 | 30 | 1L |
SHI | #2 | 3.2 / 3.2 | SHI- 4 | 2mils * 12 | 1 | 3L |
Ns | #3 | 3.2 / 3.2 | 8.9 - 6.7 | Φ0.4 * 6 | 10 | 3L |
SHI | #4 | 3.2 / 3.2 | SHI- 4 | 2mils * 12 | 1 | 1L |
Np | #5 | 3.2 / 3.2 | A -- 1 | Φ0.35 * 2 | 30 | 1L |
Nvcc | #6 | 3.2 / 3.2 | 3 -- 4 | Φ0.18 | 7 | 2L |
#7 | 连 结 两 A 点 | 2L |
反激式变压器造价信息
反激式变压器一般工作于两种工作方式 :
1. 电感电流不连续模式DCM (Discontinuous Inductor Current Mode)或称 " 完全能量转换 ": 同时储存在变压器中的所有能量在反激周期 (toff)中都转移到输出端.
2. 电感电流连续模式CCM ( Continuous Inductor Current Mode) 或称 " 不完全能量转换 " : 储存在变压器中的一部分能量在toff末保留到下一个ton周期的开始.
DCM和CCM在小信号传递函数方面是极不相同的,其波形如图3.实际上,当变换器输入电压VIN 在一个较大范围内发生变化,或是负载电流 IL在较大范围内变化时,必然跨越着两种工作方式.因此反激式转换器要求在DCM / CCM都能稳定工作.但在设计上是比较困难的.通常我们可以以DCM / CCM临界状态作设计基准.,并配以电流模式控制PWM.此法可有效解决DCM时之各种问题,但在 CCM时无消除电路固有的不稳定问题.可用调节控制环增益编离低频段和降低瞬态响应速度来解决CCM时因传递函数 " 右半平面零点 "引起的不稳定.
DCM和CCM在小信号传递函数方面是极不相同的.
DCM / CCM原副边电流波形图
实际上,当变换器输入电压VIN在一个较大范围内发生变化,或是负载电流 IL在较大范围内变化时,必然跨越着两种工作方式.因此反激式转换器要求在DCM / CCM都能稳定工作.但在设计上是比较困难的.通常我们可以以DCM / CCM临界状态作设计基准.,并配以电流模式控制PWM.此法可有效解决DCM时之各种问题,但在CCM时无消除电路固有的不稳定问题.可用调节控制环增益编离低频段和降低瞬态响应速度来解决CCM时因传递函数 " 右半平面零点 "引起的不稳定.
在稳定状态下,磁通增量ΔΦ在ton时的变化必须等于在"toff"时的变化,否则会造成磁芯饱和.
因此,
ΔΦ = VIN ton / Np = Vs*toff / Ns
即变压器原边绕组每匝的伏特/秒值必须等于副边绕组每匝伏特/秒值.
比较图3中DCM与CCM之电流波形可以知道:DCM状态下在Tr ton期间,整个能量转移波形中具有较高的原边峰值电流,这是因为初级电感值Lp相对较低之故,使Ip急剧升高所造成的负面效应是增加了绕组损耗(winding lose)和输入滤波电容器的涟波电流,从而要求开关晶体管必须具有高电流承载能力,方能安全工作.
在CCM状态中,原边峰值电流较低,但开关晶体在ton状态时有较高的集电极电流值.因此导致开关晶体高功率的消耗.同时为达成CCM,就需要有较高的变压器原边电感值Lp,在变压器磁芯中所储存的残余能量则要求变压器的体积较DCM时要大,而其它系数是相等的.
综上所述,DCM与CCM的变压器在设计时是基本相同的,只是在原边峰值电流的定义有些区别 ( CCM时 Ip = Imax - Imin ).
当开关晶体管Tr ton时,变压器初级Np有电流 Ip,并将能量储存于其中(E = Lp*Ip^2 / 2).由于Np与Ns极性相反,此时二极管D反向偏压而截止,无能量传送到负载.当开关Tr off 时,由楞次定律: (e = -N△Φ/△T)可知,变压器原边绕组将产生一反向电势,此时二极管D正向导通,负载有电流IL流通.反激式转换器之稳态波形
导通时间 ton的大小将决定Ip、Vce的幅值:
Vce max = VIN / (1-Dmax)
VIN: 输入直流电压 ; Dmax : 最大工作周期
Dmax = ton / T
由此可知,想要得到低的集电极电压,必须保持低的Dmax,也就是Dmax<0.5,在实际应用中通常取Dmax = 0.4,以限制Vcemax ≦ 2.2VIN.
开关管Tr on时的集电极工作电流Ie,也就是原边峰值电流Ip为: Ic = Ip = IL / n. 因IL = Io,故当Io一定时,匝比 n的大小即决定了Ic的大小,上式是按功率守恒原则,原副边安匝数 相等 Np*Ip = Ns*Is而导出. Ip亦可用下列方法表示:
Ic = Ip = 2Po / (η*VIN*Dmax) η: 转换器的效率
公式导出如下:
输出功率 : Po = LIp^2η / (2T)
输入电压 : VIN = L*di / dt设 di = Ip,且 1 / dt = f / Dmax,则:
VIN = L*Ip*f / Dmax 或 Lp = VIN*Dmax / (Ip*f)
则Po又可表示为 :
Po = η*VIN*f* Dmax*Ip^2 /(2f*Ip) = 1/2*η*VIN*Dmax*Ip
∴Ip = 2Po / (η*VIN*Dmax)
上列公式中 :
VIN : 最小直流输入电压 (V)
Dmax : 最大导通占空比
Lp : 变压器初级电感 (mH)
Ip : 变压器原边峰值电流 (A)
f : 转换频率 (KHZ)
反激式变压器的设计常见问题
-
当然是正激式的,变压器加电感二合一的能量一定大于同等规格变压器的能量。正激式变压器有很多, 磁芯容量看ET值主要分单端或双端正激式变压器, △B取值不一样,磁芯可工作在第一或第一三象限反激磁芯都只工作...
-
设计一般小型电源变压器;铁芯截面积A=1.25*√P(功率)。 铁芯取8500高斯 。 每伏匝数取:T=450000/8500*S(截面积) 漆包线载流量取2.5A-3.5A/mm2 ...
反激式变压器优点
反激式变压器的优点有:
1. 电路简单,能高效提供多路直流输出,因此适合多组输出要求.
2. 转换效率高,损失小.
3. 变压器匝数比值较小.
4. 输入电压在很大的范围内波动时,仍可有较稳定的输出,目前已可实现交流输入在 85~265V间.无需切换而达到稳定输出的要求.
反激式变压器缺点
反激式变压器的缺点有:
1. 输出电压中存在较大的纹波,负载调整精度不高,因此输出功率受到限制,通常应用于150W以下.
2. 转换变压器在电流连续(CCM)模式下工作时,有较大的直流分量,易导致磁芯饱和,所以必须在磁路中加入气隙,从而造成变压器体积变大.
3. 变压器有直流电流成份,且同时会工作于CCM / DCM两种模式,故变压器在设计时较困难,反复调整次数较顺向式多,迭代过程较复杂.
FLYBACK变压器设计之考量因素
1.储能能力.当变压器工作于CCM方式时,由于出现了直流分量,需加AIR GAP,使磁化曲线向 H 轴倾斜,从而使变压器能承受较大的电流,传递更多的能量.
Ve: 磁芯和气隙的有效体积.
or P = 1/2Lp (Imax2 - Imin2)
式中Imax, Imin —— 为导通周期末,始端相应的电流值.
由于反激式变压器磁芯只工作在第一象限磁滞回线,磁芯在交、直流作用下的B.H效果与AIR GAP大小有密切关联,如图4.在交流电流下气隙对ΔBac无改变效果,但对ΔHac将大大增加,这是有利的一面,可有效地减小CORE的有效磁导率和减少原边绕组的电感.
在直流电流下气隙的加入可使CORE承受更加大的直流电流去产生HDC,而BDC却维持不变,因此在大的直流偏置下可有效地防止磁芯饱和,这对能量的储存与传递都是有利的. 当反激变压器工作于CCM时,有相当大的直流成份,这时就必须有气隙.
外加的伏秒值,匝数和磁芯面积决定了B轴上ΔBac值; 直流的平均电流值,匝数和磁路长度决定了H轴上HDC值的位置. ΔBac对应了ΔHac值的范围.可以看出,气隙大ΔHac就大. 如此,就必须有足够的磁芯气隙来防止饱和状态并平稳直流成分.
反激式变压器设计步骤
例如:输入电压:AC90-264V 输出电压:19V 输出电流:3.16A 输出功率:60W 频率:70K
Step1. 选择CORE材质,确定△B
本例为ADAPTER DESIGN,由于该类型机散热效果差,故选择CORE材质应考量高Bs,低损耗及高μi材质,结合成本考量,在此选用Ferrite Core, 以TDK 之 PC40 or PC44为优选, 对比TDK DATA BOOK, 可知 PC44材质单位密度
相关参数如下: μi = 2400 ± 25% Pvc = 300KW / m2 @100KHZ ,100℃
Bs = 390mT Br = 60mT @ 100℃ Tc = 215℃
为防止X'FMR出现瞬态饱和效应, 此例以低△B设计.
选 △B = 60%Bm, 即△B = 0.6 * (390 - 60) = 198mT ≒0.2 T
Step2确定Core Size和 Type.
1> 求core AP以确定 size
AP= AW*Ae=(Pt*104)/(2ΔB*fs*J*Ku)
= [(60/0.83 60)*104]/(2*0.2*70*103*400*0.2) = 0.59cm4
式中 Pt = Po /η Po 传递功率;
J : 电流密度 A / cm2 (300~500) ; Ku: 绕组系数 0.2 ~ 0.5 .
2> 形状及规格确定.
形状由外部尺寸,可配合BOBBIN, EMI要求等决定,规格可参考AP值及形状要求而决定, 结合上述原则, 查阅TDK之DATA BOOK,可知RM10, LP32/13, EPC30均可满足上述要求,但RM10和EPC30可用绕线容积均小于LP32/13,在此选用LP32/13 PC44,其参数如下:
Ae = 70.3 mm2 Aw = 125.3mm2 AL = 2630±25% le = 64.0mm
AP = 0.88 cm4 Ve = 4498mm3 Pt = 164W ( forward )
Step3估算临界电流 IOB ( DCM / CCM BOUNDARY )
本例以IL达80% Iomax时为临界点设计变压器.
即 : IOB = 80%*Io(max) = 0.8*3.16 = 2.528 A
Step4求匝数比 n
n = [VIN(min) / (Vo Vf)] * [Dmax / (1-Dmax)] VIN(min) = 90*√2 - 20 = 107V
= [107 / (19 0.6)] *[0.5 / (1- 0.5)]
= 5.5 ≒ 6
匝比 n 可取 5 或 6,在此取 6 以降低铁损,但铜损将有所增加.
CHECK Dmax:
Dmax = n (Vo Vf) / [VINmin n (Vo Vf)]= 6*(19 0.6) /[107 6*(19 0.6)] = 0.52
Step5求CCM / DCM临
ΔISB = 2IOB / (1-Dmax) = 2*2.528 / (1-0.52) = 10.533
Step6计算次级电感 Ls 及原边电感 Lp
Ls = (Vo Vf)(1-Dmax) * Ts / ΔISB = (19 0.6) * (1-0.52) * (1/70000) / 10=12.76uH
Lp = n*n*Ls = 6*6*12.76 = 459.4 uH ≒ 460
此电感值为临界电感,若需电路工作于CCM,则可增大此值,若需工作于DCM则可适当调小此值.
Step7求CCM时副边峰值电流Δisp
Io(max) = (2ΔIs ΔISB) * (1- Dmax) / 2 ΔIs = Io(max) / (1-Dmax) - (ΔISB / 2 )
ΔIsp = ΔISB ΔIs = Io(max) / (1-Dmax) (ΔISB/2) = 3.16 / (1-0.52) 10.533 / 2=11.85A
Step8求CCM时原边峰值电流ΔIpp
ΔIpp = ΔIsp / n = 11.85 / 6 = 1.975 A
Step9确定Np、Ns
1> Np
Np = Lp * ΔIpp / (ΔB* Ae) = 460*1.975 / (0.2*70.3) = 64.6 Ts
因计算结果为分数匝,考虑兼顾原、副边绕组匝数取整,使变压器一、二次绕组有相同的安匝值,故调整 Np = 60Ts OR Np = 66Ts
考量在设定匝数比n时,已有铜损增加,为尽量平衡Pfe与Pcu,在此先选 Np = 60 Ts.
2> Ns
Ns = Np / n = 60 / 6 = 10 Ts
3> Nvcc
求每匝伏特数Va Va = (Vo Vf) / Ns = (19 0.6) / 10 = 1.96 V/Ts
∴ Nvcc = (Vcc Vf) / Va =(12 1)/1.96=6.6
Step10计算AIR GAP
lg = Np2*μo*Ae / Lp = 602*4*3.14*10-7*70.3 / 0.46 = 0.69 mm
Step11计算线径dw
1> dwp
Awp = Iprms / J Iprms = Po / η / VIN(min) = 60/0.83/107 = 0.676A
Awp = 0.676 / 4 J取4A / mm2 or 5A / mm2
= 0.1 (取Φ0.35mm*2)
2> dws
Aws = Io / J = 3.16 / 4 (Φ1.0 mm)
量可绕性及趋肤效应,采用多线并绕,单线不应大于Φ0.4, Φ0.4之Aw= 0.126mm2, 则 0.79 (即Ns采用Φ0.4 * 6)
3> dwvcc Awvcc = Iv / J = 0.1 /4
上述绕组线径均以4A / mm2之计算,以降低铜损,若结构设计时线包过胖,可适当调整J之取值.
4> 估算铜窗占有率.
0.4Aw ≧Np*rp*π(1/2dwp)2 Ns*rs*π(1/2dws)2 Nvcc*rv*π(1/2dwv)2
0.4Aw ≧60*2*3.14*(0.35/2)2 10*6*3.14 (0.4/2)2 7*3.14*(0.18/2)2
≧ 11.54 7.54 0.178 = 19.26
0.4 * 125.3 = 50.12
50.12 > 19.26 OK
Step12估算损耗、温升
求出各绕组之线长. 求出各绕组之RDC和Rac @100℃ 求各绕组之损耗功率 加总各绕组之功率损耗(求出Total值) 如 : Np = 60Ts , LP32/13BOBBIN绕线平均匝长 4.33cm
则 INP = 60*4.33 = 259.8 cm Ns = 10Ts
则 INS = 10*4.33 = 43.3 cm
Nvcc = 7Ts
则 INvc = 7 * 4.33 = 30.31cm
查线阻表可知 : Φ0.35mm WIRE RDC = 0.00268Ω/cm @ 100℃
Φ0.40mm WIRE RDC = 0.00203 Ω/cm @ 100℃
Φ0.18mm WIRE RDC = 0.0106 Ω/cm @ 100℃
R@100℃ = 1.4*R@20℃
求副边各电流值. 已知Io = 3.16A.
副边平均峰值电流 : Ispa = Io / (1-Dmax ) = 3.16 / (1- 0.52) = 6.583A
副边直流有效电流 : Isrms = √〔(1-Dmax)*I2spa〕 = √(1- 0.52)*6.5832 = 4.56A
副边交流有效电流 : Isac = √(I2srms - Io2) = √(4.562-3.162) = 3.29A
求原边各电流值 :
∵ Np*Ip = Ns*Is
原边平均峰值电流 : Ippa = Ispa / n = 6.58 / 6 = 1.097A
原边直流有效电流 : Iprms = Dmax * Ippa = 1.097 * 0.52 = 0.57A
原边交流有效电流 : Ipac = √D*I2ppa = 1.097*√0.52 = 0.79A
求各绕组交、直流电阻.
原边 : RPDC = ( lNp * 0.00268 ) / 2 = 0.348Ω
Rpac = 1.6RPDC = 0.557Ω
副边 : RSDC = ( lNS*0.00203 ) /6 = 0.0146Ω
Rsac = 1.6RSDC = 0.0243Ω
Vcc绕组 : RDC =30.31*0.0106 = 0.321Ω
计算各绕组交直流损耗:
副边直流损 : PSDC = Io2RSDC = 3.162 * 0.0146 = 0.146W
交流损 : Psac = I2sac*Rsac = 3.292*0.0234 = 0.253W
Total : Ps = 0.146 0.253 = 0.399 W
原边直流损 : PPDC = Irms2RPDC = 0.572 * 0.348 = 0.113W
交流损 : Ppac = I2pac*Rpac = 0.792*0.557 = 0.348W
忽略Vcc绕组损耗(因其电流甚小) Total Pp = 0.461W
总的线圈损耗 : Pcu = Pc Pp = 0.399 0.461 = 0.86 W
2> 计算铁损 PFe
查TDK DATA BOOK可知PC44材之△B = 0.2T 时,Pv = 0.025W / cm2
LP32 / 13之Ve = 4.498cm3
PFe = Pv * Ve = 0.025 * 4.498 = 0.112W
Ptotal = Pcu PFe = 0.6 0.112 = 0.972 W 估算温升 △t 依经验公式 △t = 23.5PΣ/√Ap = 23.5 * 0.972 / √0.88 = 24.3 ℃
估算之温升△t小于SPEC,设计OK.
Step13结构设计
查LP32 / 13 BOBBIN之绕线幅宽为 21.8mm.
考量安规距离之沿面距离不小于6.4mm.
为减小LK提高效率,采用三明治结构,其结构如下 :
X'FMR结构 :
| Np |
#1 |
3.2 / 3.2 |
2 -- A |
Φ0.35 * 2 |
30 |
1L |
| SHI |
#2 |
3.2 / 3.2 |
SHI- 4 |
2mils * 12 |
1 |
3L |
| Ns |
#3 |
3.2 / 3.2 |
8.9 - 6.7 |
Φ0.4 * 6 |
10 |
3L |
| SHI |
#4 |
3.2 / 3.2 |
SHI- 4 |
2mils * 12 |
1 |
1L |
| Np |
#5 |
3.2 / 3.2 |
A -- 1 |
Φ0.35 * 2 |
30 |
1L |
| Nvcc |
#6 |
3.2 / 3.2 |
3 -- 4 |
Φ0.18 |
7 |
2L |
| #7 |
连 结 两 A 点 |
2L |
反激式变压器的设计文献

 毕业论文-变压器的设计
毕业论文-变压器的设计
驻马店职业技术学院 毕 业 设 计 题目: 开关电源的高频变压器设计 学 生 姓 名: 徐前 学号 :080382011308 学 部 (系): 机电学部 专 业 年 级: 08 应电 指 导 教 师: 张亚兰 职称或学位:助教 2011 年 4 月 10 日 1 目 录 摘要 ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, 2 Abstract ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, 2 前言 ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, 3 1. 国内外研究现状 ,,,,,,,,,,,,,,,,,,,,,,,,, 4 2.高频变压器的基本原理及其作用 ,,,,,,,,,,,,,,,,,,, 4 3.常见的带隔离的开关电源中变压器的作用 ,,,,,,,,,,,,,,, 5 3.1 正激电路

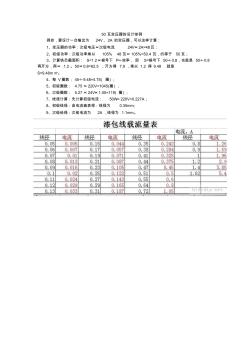 50瓦变压器的设计举例
50瓦变压器的设计举例
50 瓦变压器的设计举例 例如,要设计一台输出为 24V、2A 的变压器,可以这样计算: 1、变压器的功率:次级电压×次级电流 24V×2A=48瓦; 2、初级功率:次级功率乘以 105% 48瓦× 105%=50.4 瓦,约等于 50瓦; 3、计算铁芯截面积: S=1.2×根号下 P÷效率, 即 S=根号下 50÷0.8,也就是 50÷0.8 再开方,再× 1.2 。50×0.8=62.5 ,开方得 7.9 ,乘以 1.2 得 9.48 就是 S=9.48m㎡。 4、每 V圈数: 45÷9.48=4.75( 圈); 5、初级圈数: 4.75× 220V=1045(圈 ); 6、次级圈数: 5.27× 24V×1.05=119( 圈 ); 7、线径计算:先计算初级电流: 50W÷220V=0.227A; 8、初级线径:由电流查表得:线径为 0.35mm; 9、次级经径:次级电流为 2A,
图1-a是反激式变压器开关电源的简单工作原理图, 图1-a中,ui是开关电源的输入电压,t是开关变压器,k是控制开关,c是储能滤波电容,r是负载电阻。图1-b是反激式变压器开关电源的 电压输出波形。 把图1-a与图1-16-a进行比较,如果我们把图1-16-a中开关变压器次级线圈的同名端对调一下,原来变压器输出电压的正、负极性就会 完全颠倒过来,图1-b所示的电压输出波形基本上就是从图1-16-b的波形颠倒过来的。不过,因为图1-16-b的波形对应的是纯电阻负载,而图 1-b的负载是一个储能滤波电容和一个电阻并联。由于储能滤波电容的容量很大,其两端电压基本不变,变压器次级线圈输出电压uo相当于被整流二极管 和输出电压uo进行限幅,因此,图1-16-b中输出电压uo的脉冲尖峰完全被削除,被限幅后的剩余电压幅值正好等于输出电压uo的最大值up,同时也等 于变压器次级线圈输出电压uo的半波平均值upa。
图1-a是反激式变压器开关电源的简单工作原理图, 图1-a中,ui是开关电源的输入电压,t是开关变压器,k是控制开关,c是储能滤波电容,r是负载电阻。图1-b是反激式变压器开关电源的 电压输出波形。 把图1-a与图1-16-a进行比较,如果我们把图1-16-a中开关变压器次级线圈的同名端对调一下,原来变压器输出电压的正、负极性就会 完全颠倒过来,图1-b所示的电压输出波形基本上就是从图1-16-b的波形颠倒过来的。不过,因为图1-16-b的波形对应的是纯电阻负载,而图 1-b的负载是一个储能滤波电容和一个电阻并联。由于储能滤波电容的容量很大,其两端电压基本不变,变压器次级线圈输出电压uo相当于被整流二极管 和输出电压uo进行限幅,因此,图1-16-b中输出电压uo的脉冲尖峰完全被削除,被限幅后的剩余电压幅值正好等于输出电压uo的最大值up,同时也等 于变压器次级线圈输出电压uo的半波平均值upa。
反激式开关电源在控制开关接通期间不向负载提供功率输出,仅在控制开关关断期间才把存储能量转化成反电动势向负载提供输出;当控制开关的占空比为0.5时,变压器次级线圈输出电压的平均值ua约等于电压最大值up(用半波平均值upa代之)的二分之一;而流过负载的电流io(平均电流)正好等于流过变压器次级线圈最大电流的四分之一。 当反激式开关电源当控制开关的占空比为0.5时,电压脉动系数sv约等于2或大于2,而电流脉动系数si约等于4。反激式开关电源的电压脉动系数与正激式变压器开关电源的电压脉动系数基本相同,但电流脉动系数比正激式变压器开关电源的电流脉动系数大两倍。由此可知,反激式开关电源的电压和电流输出特性要比正激式变压器开关电源差。特别是,反激式开关电源使用的时候,为了防止电源开关管过压击,其占空比一般都取得小于0.5,此时,流过变压器次级线圈的电流会出现断流,电压和电流的脉动系数都会增加,其电压和电流的输出特性将变得更差。 由于反激式开关电源仅在控制开关关断期间才向负载提供能量输出,当负载电流出现变化时,开关电源不能立刻对输出电压或电流产生反应,而需要等到下个工作周期时,通过输出电压取样和调宽控制电路的作用,开关电源才开始对已经过去了的事件进行反应(即改变占空比),因此,反激式开关电源输出电压的瞬态控制特性相对来说比较差。有时,当负载电流变化的频率或相位正好与取样、调宽控制电路输出电压的延时特性在相位保持一致的时候,反激式开关电源输出电压可能会产生抖动。这种情况在电视机开关电源中最容易出现。 反激式开关变压器的铁心一般都需要留一定的气隙,一方面是为了防止变压器的铁心因流过变压器初级线圈的电流过大,容易产生磁饱和;另一方面是因为变压器的输出功率大小,需要通过调整变压器铁心的气隙和初级线圈的匝数,来调整变压器初级线圈的电感量大小。因此,反激式开关变压器初、次级线圈的漏感都比较大,从而会降低开关变压器的工作效率,并且漏感还会产生反电动势,容易把开关器件击穿。 反激式变压器开关电源的优点是电路比较简单,正反激式变压器开关电源少用一个大储能滤波电感,以及一个续流二极管,因此,反激式变压器开关电源的体积要比正激式变压器开关电源的体积小,且成本也要降低。此外,反激式变压器开关电源输出电压受占空比的调制幅度,相对于正激式变压器开关电源来说要高很多,因此,反激式变压器开关电源要求调控占空比的误差信号幅度比较低,误差信号放大器的增益和动态范围也比较小。由于这些优点,目前,反激式变压器开关电源在家电领域中还是被广泛使用。
- 相关百科
- 相关知识
- 相关专栏
- 热电偶检定炉温度场测试技术规范
- 旱矿磁选机
- 热电阻校验仪
- 金刚石压腔高温高压实验技术及其应用
- 铠装热电偶校准规范
- 清水浦大桥
- 电站热电偶
- 高温炉壁热电偶
- 平衡浓度
- 太阳能一体化热电偶
- 方正A600
- JJG344-2005镍铬-金铁热电偶检定规程
- 无缝钢管的制造方法
- 质子平衡
- 石油化工专用热电偶
- 缓冲溶液
- 张潘明污水处理厂初步设计说明书(水质工程学课程)
- 云南洱海桃溪河口净化工程的设计思路及初步净化效果
- 增设钢牛腿在连续独柱墩桥梁抗倾覆加固设计中的应用
- 智能建筑火灾自动报警与消防联动系统设计及应用效果
- 余杭某供电营业所生产营业用房工程建筑设计招标文件
- 中国建筑抗震设计规范的演变与展望
- 中国恩菲工程技术有限公司中国有色工程设计总院
- 园林景观及配套设施标工程施工组织设计建筑施工
- 再谈VRV空调系统设计与施工中有关问题的解决方法
- 有关CAD技术在水利工程设计中的实际应用方法
- 中、小跨径钢筋混凝土拱桥现浇支架(拱架)设计指南
- 中国国家博物馆改扩建设计回顾及学术研讨会
- 影响我国公路桥梁板式橡胶支座质量的因素及应对措施
- 张力式电子围栏周界防范报警系统设计原理及应用现状
- 医药工业空调带转轮热回收装置的工程设计和节能分析
- 园林工程设计